
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Момент силы
Моментом  силы
силы  относительно неподвижной точкиО называется физическая величина, определяемая векторным произведением радиуса-вектора
относительно неподвижной точкиО называется физическая величина, определяемая векторным произведением радиуса-вектора 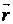 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу  (рис. 4.1):
(рис. 4.1):
 .
.
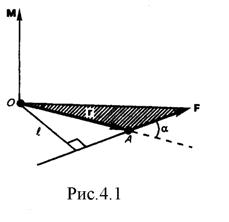 Здесь
Здесь  – аксиальный вектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– аксиальный вектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 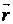 к
к  .
.
Модуль момента силы
 , (4.1)
, (4.1)
где  – угол между
– угол между 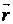 и
и  ; r sin
; r sin  = l – плечо силы – кратчайшее расстояние от оси вращения до точки приложения силы.
= l – плечо силы – кратчайшее расстояние от оси вращения до точки приложения силы.
Пара сил
Если на тело действует несколько сил, равнодействующая которых равна нулю, а результирующий момент относительно какой-либо оси не равен нулю, то тело не останется в равновесии. Так будет, например, если на тело действуют две равные и противоположные силы, не лежащие на одной прямой.
Такие две силы, совместно действующие на тело, называют парой сил. Если тело закреплено на оси, то при действии на него пары сил оно начнет вращаться вокруг этой оси.
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Действительно, пусть О – произвольная ось, перпендикулярная к плоскости, в которой лежит пара сил (рис. 4.2). Суммарный момент М равен M = F·OA + F·OB = F (OA + OB) = F · l, где l – расстояние между силами, составляющими пару.
 Силы, действующие на твердое тело, могут вызвать как поступательное, так и вращательное движение тела. Чтобы тело находилось в равновесии, необходимо выполнение следующих условий:
Силы, действующие на твердое тело, могут вызвать как поступательное, так и вращательное движение тела. Чтобы тело находилось в равновесии, необходимо выполнение следующих условий:
– равнодействующая всех действующих на тело сил равна нулю;
– сумма всех моментов сил равна нулю.
Если силы лежат в одной плоскости, получаем следующие условия равновесия:
 ; (4.2)
; (4.2)
 . (4.3)
. (4.3)
Простые механизмы
Простые механизмы служат для того, чтобы изменять величину или направление приложенных сил при неизменной затрате работы. Эти механизмы не могут изменить величину работы. Если уменьшается приложенная сила, то должно увеличиться перемещение. В силу вступает «золотое правило механики»: то, что удается выиграть в силе, приходится проигрывать в перемещении.
Рычагом называется твердое тело, вращающееся вокруг некоторой оси. У одноплечного рычага ось расположена на одном из концов и силы, действующие на него, антипараллельны. У двуплечного рычага ось расположена между точками приложения сил и силы параллельны (рис. 4.3).
 Если F 1 – сила, уравновешивающая нагрузку, F 2 – нагрузка, l 1 – плечо силы, равное расстоянию по перпендикуляру от точки опоры до линии действия силы F 1, l 2 – плечо нагрузки, равное расстоянию по перпендикуляру от точки опоры до линии действия нагрузки F 2, то, согласно правилу рычага,
Если F 1 – сила, уравновешивающая нагрузку, F 2 – нагрузка, l 1 – плечо силы, равное расстоянию по перпендикуляру от точки опоры до линии действия силы F 1, l 2 – плечо нагрузки, равное расстоянию по перпендикуляру от точки опоры до линии действия нагрузки F 2, то, согласно правилу рычага,
F 1 l 1 = F 2 l 2. (4.4)
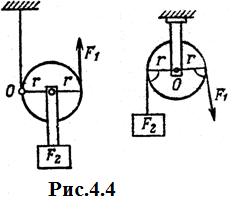 Неподвижный блок действует аналогично равноплечному рычагу (рис. 4.4). Моменты сил, действующие с обеих сторон блока, одинаковы, соответственно одинаковы и силы, создающие эти моменты. У неподвижного блока сила равна нагрузке F 1 = F 2, то есть неподвижный блок изменяет только направление действия силы.
Неподвижный блок действует аналогично равноплечному рычагу (рис. 4.4). Моменты сил, действующие с обеих сторон блока, одинаковы, соответственно одинаковы и силы, создающие эти моменты. У неподвижного блока сила равна нагрузке F 1 = F 2, то есть неподвижный блок изменяет только направление действия силы.
Подвижный блок действует аналогично одноплечному рычагу. Относительно центра вращения О действуют моменты сил, которые при равновесии должны быть равны: F 1 2 r = F 2 r. Отсюда,  , то есть сила равна половине нагрузки. Подвижный блок изменяет только величину силы.
, то есть сила равна половине нагрузки. Подвижный блок изменяет только величину силы.
Момент инерции
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
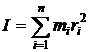 . (4.5)
. (4.5)
В случае непрерывного распределения масс эта сумма сводится к интегралу
 , (4.6)
, (4.6)
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 4.5).
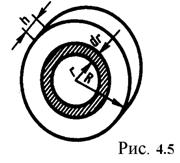 Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра
Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра  (так как dr < < r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm – масса всего элементарного цилиндра; его объем
(так как dr < < r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm – масса всего элементарного цилиндра; его объем  dr. Если
dr. Если 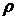 – плотность материала, то
– плотность материала, то 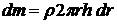 и
и 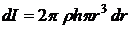 . Тогда момент инерции сплошного цилиндра
. Тогда момент инерции сплошного цилиндра
 ,
,
но так как  – объем цилиндра, то его масса
– объем цилиндра, то его масса  , а момент инерции
, а момент инерции
 .
.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно любой оси вращения О равен моменту его инерции IC относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния a 2 между осями:
I = IC + ma 2. (4.7)
Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m – масса тела).
| Таблица 1 | ||
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR 2 |
| Сплошной цилиндр или диск радиусом R | То же | (1/2) mR 2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12) ml 2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3) ml 2 |
| Шар радиусом R | Ось проходит через центр шара | (2/5) mR 2 |
Не нашли, что искали? Воспользуйтесь поиском: