Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 4.6).

Мысленно разобьем это тело на материальные точки с элементарными массами m ₁, m ₂, ..., т_n, находящиеся на расстоянии r ₁, r ₂, ..., r_n от оси вращения. При вращении твердого тела относительно не­подвижной оси отдельные его элементарные объемы массами m_i опишут окружности различных радиусов r_i, и имеют различные линейные скорости u_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:

. (4.8)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

или .

Используя выражение (4.5), получим

,

где – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела

. (4.9)

Из сравнения формулы (4.6) с выражением для кинетической энергии тела, движущегося поступательно (), следует, что момент инерции вращательного движения – мера инертности тела. Формула (4.9) справедлива для тела, вращающегося вокруг неподвижной оси.

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

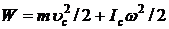, (4.10)

где m – масса катящегося тела; – скорость центра масс тела; –момент инерции тела относительно оси, проходящей через его центр масс; – угловая скорость тела.

Не нашли, что искали? Воспользуйтесь поиском: