
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
1 страница. ФГБОУ ВПО «Московский государственный строительный университет»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «Московский государственный строительный университет»
Кафедра информатики и прикладной математики
Осмоловский Н.П., Осипов Ю.В.
КОНСПЕКТ лекциЙ
По линейной алгебре и аналитической геометрии
Учебное пособие
Москва – 2013
Осмоловский Н.П., Осипов Ю.В. Конспект лекций по линейной алгебре и аналитической геометрии. / Моск. гос. строит. ун-т. М.: 2013. – 125 с.
Методические указания предназначены для студентов всех направлений ИЭУИС, изучающих аналитическую геометрию и линейную алгебру в курсах “Линейной алгебры” и “Математики”. Излагаемый теоретический материал представлен в виде 18 лекций в соответствии с учебными планами университета.
Рецензенты:
проф., д-р техн. наук Коренева Е.Б. (МГСУ)
доц., канд. физ.-мат. наук Демидович В.Б. (мехмат МГУ)
Лекция 1.
Тема: Системы линейных алгебраических уравнений.
Правило Крамера. Определители.
1. Система двух уравнений с двумя неизвестными. Определитель 2-го порядка. Правило Крамера.
Рассмотрим линейную систему
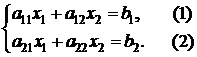
Говорят, что
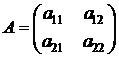
– матрица системы,
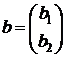
– вектор правых частей,
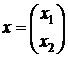
– неизвестный вектор.
Как решить систему в общем виде? Найдем х 1. Для этого умножим уравнение (1) на а 22, а (2) – на а 12 и вычтем из первого уравнения второе. В результате х 2 пропадет (т.к. коэффициенты при х 2 окажутся равными), и мы получим:
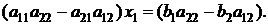 (3)
(3)
Обозначим
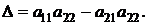
Это – определитель квадратной матрицы второго порядка


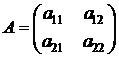 .
.
Элементы а 11 и а 22 образуют главную диагональ матрицы, а элементы а 12 и а 21 – побочную.
Определитель 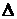 равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Итак, определитель – это число, соответствующее данной матрице (вычисляемое по определенному правилу). Его обозначают еще так
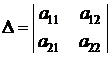
(прямые вертикальные «палочки» обозначают определитель, т.е. число, в отличие от круглых скобок, обозначающих матрицу, т.е. таблицу), или так

(det – от слова детерминант, т.е. определитель).
Рассмотрим выражение в правой части уравнения (3). Это определитель матрицы
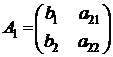 ,
,
полученной из матрицы А заменой первого столбца на столбец свободных членов. Обозначим его 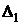 . Итак,
. Итак,
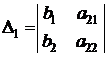 .
.
Уравнение (3) приняло вид
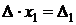 .
.
Пусть  . Тогда
. Тогда
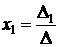 . (4)
. (4)
Аналогично, можно показать (сделайте это!), что
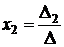 , (5)
, (5)
где 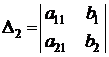 , то есть определитель
, то есть определитель  получен из
получен из 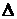 заменой второго столбца на столбец свободных членов. Формулы (4) и (5) носят название правила Крамера. Мы доказали следующую теорему.
заменой второго столбца на столбец свободных членов. Формулы (4) и (5) носят название правила Крамера. Мы доказали следующую теорему.
Теорема 1. Если определитель матрицы системы отличен от нуля, то система имеет единственное решение, которое находится по правилу Крамера.
Эту теорему ты доказали для  , т.е. для системы двух уравнений с двумя неизвестными. Справедлива ли она для произвольного n? Точнее, можно ли для произвольного n так сформулировать понятие определителя, чтобы правило Крамера сохраняло силу? Мы хотим, чтобы для произвольного n имели место формулы:
, т.е. для системы двух уравнений с двумя неизвестными. Справедлива ли она для произвольного n? Точнее, можно ли для произвольного n так сформулировать понятие определителя, чтобы правило Крамера сохраняло силу? Мы хотим, чтобы для произвольного n имели место формулы:
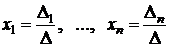 , (6)
, (6)
где 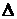 – определитель матрицы системы, а
– определитель матрицы системы, а 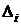 получается из
получается из  заменой i -го столбца на столбец свободных членов. Оказывается можно. Как это делается – мы опишем для определителей 3-го порядка.
заменой i -го столбца на столбец свободных членов. Оказывается можно. Как это делается – мы опишем для определителей 3-го порядка.
2. Определитель 3-го порядка. Миноры элементов. Разложение определителя по строке или столбцу.
Рассмотрим квадратную матрицу 3-го порядка:
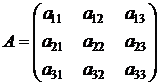 .
.
Ее определитель есть число, вычисленное по правилу
 .
.
Коэффициент при а 11 в этой формуле называется минором этого элемента (от слова «младший»). Вообще, минор элемента аij – это определитель матрицы, получаемой из матрицы А вычеркиванием i -й строки и j -го столбца. Например, определитель
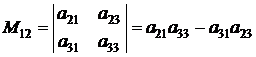
есть минор элемента а 12 (вычеркивается 1-я строка и 2-й столбец, в которых содержится элемент а 12). Итак,
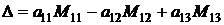 , (7)
, (7)
где Mij – миноры элементов аij. Формула (7) для вычисления определителя называется разложением определителя по первой строке.
Положим
 .
.
Назовем Аij алгебраическим дополнением к элементу аij. Ясно, что
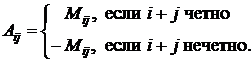
Вычисляя алгебраические дополнения, относящиеся к данной строке (столбцу), следует брать миноры попеременно то с плюсом, то с минусом.
С помощью алгебраических дополнений формулу (7) можно записать в виде
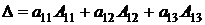 , (8)
, (8)
т.е. определитель равен сумме произведений элементов первой строки на их алгебраические дополнения.
Можно доказать, что это верно для произвольной строки или столбца.
Теорема 2. Определитель равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения.
Например (разлагаем по последней строке),
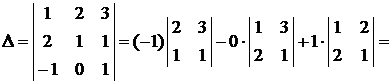
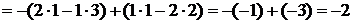 .
.
Разложите по первой строке и получите тот же ответ.
Разлагая определитель 3-го порядка по 1-й строке, покажите что
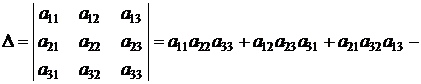
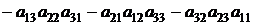 . (9)
. (9)
Схематически это выражение можно изобразить с помощью картинки (правило треугольников).
(+) (–)
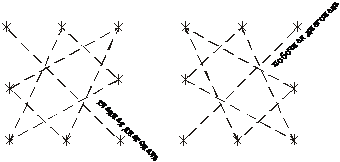
Поясните эти картинки. (Слева берется главная диагональ и треугольники, у которых сторона параллельна главной, справа – побочная и треугольники, у которых одна сторона ей параллельна).
Обратите внимание, что в формуле (9) стоят суммы произведений (с плюсом или с минусом) элементов взятых из разных строк и разных столбцов матрицы. Так будет и при вычислении определителей произвольного порядка n. А что такое определитель порядка n?
4. Определитель порядка n.
Разлагая определитель 3-го порядка по строке (столбцу), мы сводим его вычисление к вычислению определителей 2-го порядка.
Аналогично, определитель 4-го порядка можно вычислить, разлагая его по строке (столбцу) и выражая через определители 3-го порядка.
Умея вычислять определители 4-го порядка, мы сможем вычислить и определитель 5-го порядка. И так далее. По индукции мы можем дойти до произвольного порядка n. При этом результат не будет зависеть от того, разложением по какой строке или столбцу на каждом шаге мы пользуемся.
5. Правило Крамера (общий случай).
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
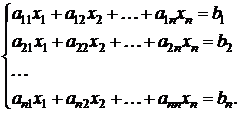 . (10)
. (10)
Здесь
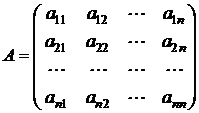
– матрица системы,
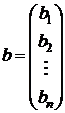
– вектор (столбец) правых частей,
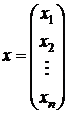
– вектор (столбец) неизвестных.
По определению вектор
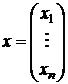
– решение системы, если при подстановке х 1, х 2,..., хn все уравнения обращаются в равенства.
Теорема (правило Крамера). Пусть определитель матрицы системы
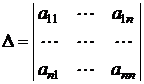
отличен от нуля. Тогда система имеет единственное решение, которое вычисляется по формулам
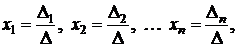
где определители 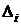 получаются из
получаются из 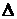 заменой i -го столбца на столбец свободных членов (i = 1, 2,..., n).
заменой i -го столбца на столбец свободных членов (i = 1, 2,..., n).
6. Свойства определителей.
1о. Определитель не меняется, если все его строки заменить соответствующими столбцами (с теми же номерами). Эта операция называется «транспонирование» – замена строк столбцами. Следовательно, все, что верно для строк определителя, верно и для его столбцов.
Пример:
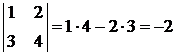 ,
, 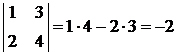 .
.
2о. Перестановка двух строк (столбцов) влечет изменение знака определителя.
Пример: (см. предыдущий пример)
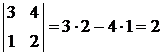 .
.
3о. При умножении всех элементов строки (столбца) на число определитель умножается на это число.
Пример:
 .
.
4о. Определитель не меняется при добавлении к элементам строки соответствующих элементов другой строки, умноженных на число. То же верно для столбцов.
Пример: из 1-й строки вычитаем вторую, умноженную на 2
 .
.
5о. Определитель, две строки (столбца) которого совпадают, равен нулю.
Лекция 2.
Тема: Векторная алгебра
1. Основные понятия.
Вектор в пространстве – направленный отрезок.

Это – изображения одного и того же вектора, поскольку их (изображения) можно совместить при помощи параллельного переноса. Вектор определяется длиной и направлением. Длина вектора 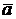 называется также его модулем и обозначается
называется также его модулем и обозначается 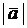 .
.
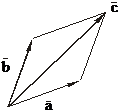
Векторы складываются по правилу параллелограмма: 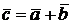
 или так:
или так: 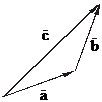
Соответственно, вектор 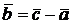 направлен от
направлен от 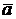 к
к  .
.
При умножении вектора на число его длина умножается на модуль числа, а направление сохраняется, если число положительно, и меняется на противоположное, если число отрицательно.
При этом получается коллинеарный вектор (т.е. вектор с тем же или противоположным направлением). Если 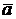 – ненулевой вектор, то вектор
– ненулевой вектор, то вектор 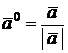 имеет то же направление и длину 1. Он называется ортом вектора
имеет то же направление и длину 1. Он называется ортом вектора 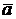 . Векторы называются компланарными, если они параллельны одной плоскости (или лежат в одной плоскости). Например, векторы
. Векторы называются компланарными, если они параллельны одной плоскости (или лежат в одной плоскости). Например, векторы 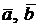 и
и 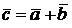 всегда компланарны.
всегда компланарны.
Пусть 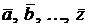 – векторы,
– векторы, 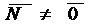 – числа. Вектор
– числа. Вектор 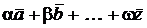 называется линейной комбинацией векторов
называется линейной комбинацией векторов 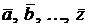 , а числа
, а числа 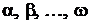 – коэффициентами линейной комбинации.
– коэффициентами линейной комбинации.
Введем в пространстве декартову прямоугольную систему координат.
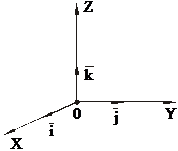
Пусть 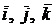 – единичные векторы (орты), направленные вдоль координатных осей X, Y, Z соответственно. Предполагается, что если смотреть с конца вектора
– единичные векторы (орты), направленные вдоль координатных осей X, Y, Z соответственно. Предполагается, что если смотреть с конца вектора 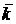 , то движение вектора
, то движение вектора 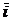 к вектору
к вектору  по короткому пути происходит против часовой стрелки. В этом случае говорят, что
по короткому пути происходит против часовой стрелки. В этом случае говорят, что 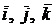 правая тройка векторов, и систему координат OXYZ также называют правой. В дальнейшем мы рассматриваем только правые прямоугольные системы.
правая тройка векторов, и систему координат OXYZ также называют правой. В дальнейшем мы рассматриваем только правые прямоугольные системы.
Пусть 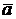 есть вектор, соединяющий точки М 1(x 1, y 1, z 1) и М 2(x 2, y 2, z 2) в пространстве (М 1 – начало, М 2 – конец).
есть вектор, соединяющий точки М 1(x 1, y 1, z 1) и М 2(x 2, y 2, z 2) в пространстве (М 1 – начало, М 2 – конец).
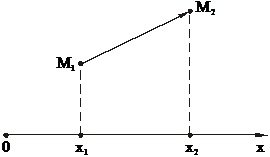
Тогда
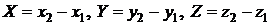
– проекции вектора на координатные оси. Они называются координатами вектора 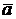 в заданной системе координат. По координатам вектор однозначно определяется. Поэтому мы будем писать:
в заданной системе координат. По координатам вектор однозначно определяется. Поэтому мы будем писать:
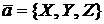 .
.
Фигурные скобки пишутся вместо круглых, чтобы отличить координаты вектора от координат точки.
Такое обозначение не является общепринятым в математике, а используется, в основном, в задачнике Д.В. Клетеника, которым мы пользуемся. На первых порах мы также будем использовать обозначения { } для координат вектора. Имеет место также представление: 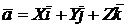 . По теореме Пифагора, применяемой дважды (как?), имеем
. По теореме Пифагора, применяемой дважды (как?), имеем
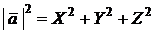 .
.
Кроме того, очевидно,
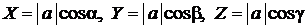 ,
,
где 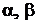 и
и 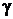 – углы между
– углы между 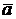 и координатными осями X, Y, Z соответственно. Следовательно,
и координатными осями X, Y, Z соответственно. Следовательно,
 .
.
Вектор 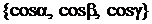 , составленный из направляющих косинусов, служит ортом вектора
, составленный из направляющих косинусов, служит ортом вектора 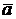 , т.е.
, т.е.
 .
.
Сложение векторов и умножение вектора на скаляр в координатной форме происходит покоординатно:
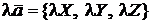 ,
,
и если
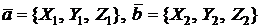 ,
,
то

(отметим, что знак «=» здесь стоит условно, ибо слева мы имеем вектор, а справа – набор его координат, который вектор задает, но мы договорились отождествлять вектор с набором).
2. Скалярное произведение.
Определение. Пусть 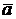 и
и 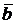 – векторы. Их скалярное произведение – это число, обозначаемое
– векторы. Их скалярное произведение – это число, обозначаемое  , или
, или 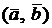 , или
, или 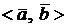 и вычисляемое так:
и вычисляемое так:
 ,
,
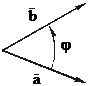
где  – угол между
– угол между 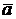 и
и 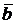 .
.
В координатной форме скалярное произведение векторов
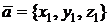 и
и 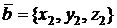
вычисляется так:
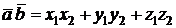 ,
,
т.е. скалярное произведение равно сумме произведений соответствующих координат.
Последним определением мы и будем пользоваться на практике. Не трудно доказать эквивалентность двух определений. Можно также доказать следующие свойства скалярного произведения:
1о. 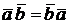 (коммутативность).
(коммутативность).
2о. 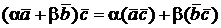 (линейность по первой компоненте, откуда следует и линейность по второй).
(линейность по первой компоненте, откуда следует и линейность по второй).
3о. 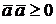 , причем,
, причем, 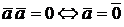 , где
, где 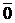 – нулевой вектор {0,0,0}.
– нулевой вектор {0,0,0}.
Отметим, что 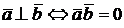 (поскольку
(поскольку 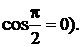 В координатной форме условие перпендикулярности векторов выглядит так:
В координатной форме условие перпендикулярности векторов выглядит так:
 .
.
Скалярное произведение позволяет вычислить угол  между векторами, заданными своими координатами. Из определения скалярного произведения для ненулевых векторов
между векторами, заданными своими координатами. Из определения скалярного произведения для ненулевых векторов 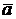 и
и 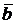 следует, что
следует, что
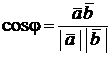 ,
,
или
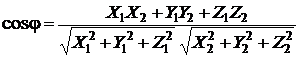 .
.
3. Векторное произведение.
Определение. Пусть 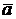 и
и 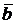 – векторы. Их векторное произведение – это вектор
– векторы. Их векторное произведение – это вектор  , обозначаемый
, обозначаемый 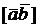 и такой, что
и такой, что
(1) 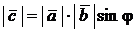 , где
, где  – угол между
– угол между 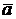 и
и 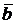 ,
,
(2) 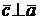 и
и 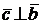 , т.е.
, т.е. 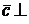 плоскости векторов
плоскости векторов 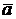 и
и 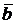 ,
,
(3) 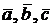 образуют правую тройку.
образуют правую тройку.
Пусть
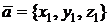 ,
, 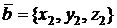 .
.
В координатной форме векторное произведение вычисляется так:
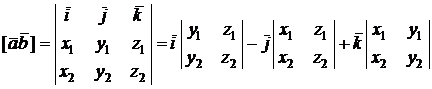 ,
,
т.е. координатами вектора 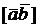 служат определители:
служат определители:
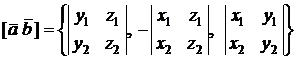 .
.
Мы не договаривались рассматривать определители, у которых в первой строке стоят не числа, а векторы! Но пользоваться такой записью удобно (причем, следует использовать именно разложение по первой строке).
При решении задач именно таким способом и вычисляют векторное произведение.
Очевидно, модуль векторного произведения равен площади параллелограмма, построенного на векторах 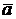 и
и 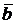 , что вытекает из определения:
, что вытекает из определения:
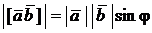 .
.
Отметим следующие свойства векторного произведения:
1о. 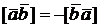 – антикоммутативность (в отличие от скалярного произведения, где имеет место коммутативность),
– антикоммутативность (в отличие от скалярного произведения, где имеет место коммутативность),
2о. 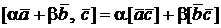 – линейность по первой компоненте.
– линейность по первой компоненте.
Аналогично, имеет место линейность и по второй компоненте.
Отметим также, что 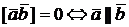 .
.
Лекция 3.
Тема: Векторная алгебра (продолжение)
4. Смешанное произведение.
Определение. Смешанным произведением векторов 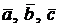 называется число
называется число 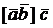 (т.е. векторное произведение
(т.е. векторное произведение 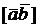 , представляющее собой вектор, скалярно умножается на вектор
, представляющее собой вектор, скалярно умножается на вектор  которое обозначается
которое обозначается 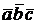 . Итак,
. Итак,
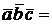
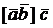 .
.
Можно доказать, что
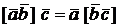 .
.
У смешанного произведения имеется следующий важный геометрический смысл. Пусть V – объем произвольного параллелепипеда, построенного на 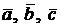 как на сторонах:
как на сторонах:

Тогда

Следовательно,
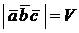 .
.
(Вы можете понять это самостоятельно. Следует учесть, что 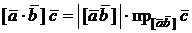 . Первый множитель есть площадь основания, а второй, взятый по модулю, равен высоте параллелепипеда. Поясните это подробнее.)
. Первый множитель есть площадь основания, а второй, взятый по модулю, равен высоте параллелепипеда. Поясните это подробнее.)
Отсюда вытекает следующее свойство смешанного произведения:  компланарны, т.е. параллельны одной плоскости. (Здесь мы считаем, что если среди
компланарны, т.е. параллельны одной плоскости. (Здесь мы считаем, что если среди 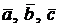 есть два коллинеарных вектора или (и) один из них нулевой, то
есть два коллинеарных вектора или (и) один из них нулевой, то 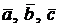 автоматически компланарны.)
автоматически компланарны.)
Смешанное произведение в координатной форме вычисляется так. Пусть
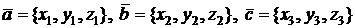 .
.
Тогда
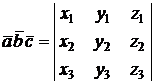 .
.
(Эту формулу вы можете легко получить, воспользовавшись соответствующими формулами для вычисления векторного произведения 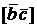 и скалярного произведения
и скалярного произведения 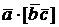 в координатной форме.)
в координатной форме.)
Отсюда вытекает геометрический смысл определителя 3-го порядка: по модулю он равен объему параллелепипеда, построенного на векторах-строках определителя (поскольку определитель не меняется при транспонировании, то вектора-строки можно заменить на вектора-столбцы). В частности, равенство нулю определителя 3-го порядка означает компланарность его вектор-строк (вектор-столбцов).
Не нашли, что искали? Воспользуйтесь поиском: