5 страница. Наборам е1, , еn-r свободных переменных соответствуют векторы

.

Наборам е ₁,..., е_{n - r} свободных переменных соответствуют векторы

,

составляющие базис в L. Их линейная комбинация

(5)

есть произвольный вектор из L. Запись (5) называется общим решением в векторной форме системы (2).

Убедитесь в том, что расписав (5) покоординатно, мы получаем (4) – общее решение в координатной форме.

Итак, размерность подпространства L есть n - r, где . Чем меньше rank А, тем большую размерность имеет L и наоборот. В случае, когда (т.е. А имеет «полный ранг»), , т.е. L имеет нулевую размерность, и, значит, состоит лишь из нулевого вектора . В этом случае (2) имеет единственное нулевое решение.

Вопрос: может ли (2) иметь ровно два решения? А три?

Пример:

Матрица системы

уже имеет ступенчатый вид. Значит прямой ход метода Гаусса делать не нужно. Зависимые переменные – это х ₁ и х ₃ (соответствуют угловым элементам матрицы), свободные – х ₂ и х ₄.

Перенесем члены со свободными переменными вправо:

Обратный ход метода Гаусса: подставляем в первое уравнение:

.

Итак:

– общее решение в координатной форме.

Запишем общее решение в векторной форме. Возьмем стандартный базис в R ²:

.

Положим:

1) .

Получим

;

2)

Получим

.

Общее решение:

.

Лекция 10.

Тема: Системы линейных алгебраических уравнений (продолжение)

1. Неоднородные системы.

Мы научились находить общее решение однородной системы. Перейдем теперь к неоднородным. Процедура получения общего решения (в координатной и векторной формах) для них будет весьма похожей.

Пусть имеется система

,

или, в координатной форме,

(1)

Выпишем расширенную матрицу системы:

.

Приведем ее к ступенчатому виду. Возможны два случая:

а) В последнем столбце ( -ом) имеется угловой элемент. В этом случае ранг расширенной матрицы оказался на 1 больше ранга матрицы А, и, значит, по теореме Кронекера–Капелли система несовместна. Этому случаю соответствует картинка:

б) В последнем ( -ом) столбце угловой элемент отсутствует. В этом случае , т.е. ранги матрицы А и расширенной матрицы совпадают. По теореме Кронекера–Капелли решение есть. Картинка имеет вид:

Найдем решение системы. Как и раньше, переменные, соответствующие угловым элементам, назовем зависимыми, остальные – свободными. Выпишем систему, соответствующую ступенчатому виду расширенной матрицы (она эквивалентна исходной системе) и все члены, содержащие свободные переменные, перенесем вправо. В левой части останутся зависимые переменные с коэффициентами, образующими верхнетреугольную матрицу. Система примет вид:

Пусть для простоты х ₁,..., х_r – зависимые, а х_{r+ 1},..., х_n – свободные. Тогда система имеет вид:

На этом завершаем прямой ход метода Гаусса. Теперь сделаем обратный ход. Из последнего уравнения выражаем х_r через свободные переменные и подставляем полученное выражение в предпоследнее уравнение. Тогда предпоследнее уравнение позволяет выразить х_{r -1} через свободные переменные. Полученные выражения для х_r, х_{r -1} используем в 3-м с конца (предпредпоследнем) уравнении. Получаем выражение для х_{r -2}. И так далее. В результате приходим к системе вида

(2)

Эта система эквивалентна исходной. Она называется общим решением системы, записанным в координатной форме.

Особо отметим случай, когда , т.е. rank А максимален и равен числу переменных n. В этом случае свободных переменных нет и мы получаем единственное решение

или в векторной форме

.

Если же , т.е. свободные переменные присутствуют, система имеет бесконечное множество решений, определяемых значениями свободных переменных. Система (2) служит хорошей формой представления общего решения: свободные переменные х_{r+ 1},..., х_n принимают произвольные значения, а зависимые х ₁,..., х_r – соответствующие значениям свободных переменных и определяемые по формулам (2). Чтобы подчеркнуть этот факт, присвоим свободным переменным значения, равные произвольным константам с ₁,..., с_{n - r} соответственно: , и перепишем систему (2) в виде:

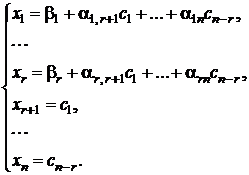(3)

Как и в случае однородной системы общее решение (2) можно представить в векторной форме. Для этого сначала находим общее решение в векторной форме соответствующей однородной системы

(4)

Чтобы его получить, нет нужды повторять заново всю процедуру для однородной системы. Достаточно в (2) заменить нулями. Получим систему

(5)

представляющую собой общее решение в координатной форме однородной системы (4). Придавая свободным переменным х_{r+ 1},..., х_n значения координат векторов

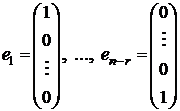
(составляющих стандартный базис в пространстве R^{n - r} свободных переменных), получаем с помощью (5) векторы

(6)

образующие базис в подпространстве L решений однородной системы (4).

Линейная комбинация

векторов этого базиса есть общее решение в векторной форме однородной системы, то есть «произвольный вектор подпространства L (сокращение «оо» означает: общее однородной).

Остается найти частное решение неоднородной системы (1). Для этого проще всего положить в (2) значения свободных переменных равными нулю:

.

Получим с помощью (2) вектор:

(7)

(сокращение «чн» означает: частное неоднородной). Как мы знаем, общее решение неоднородной системы есть сумма частного решения неоднородной и общего решения однородной системы:

(«он» – общее неоднородной), или, подробнее,

, (8)

где с ₁,..., с_{n - r} – произвольные постоянные. Формула (8) есть общее решение неоднородной системы в векторном виде (в векторной форме). Здесь определены формулами (6), а x ^чн – формулой (7). Множество всех решений неоднородной системы есть сдвиг подпространства L всех решений однородной системы (общий элемент которого есть линейная комбинация ) на произвольный вектор x ^чн, представляющий собой частное решение неоднородной системы (результат сдвига не зависит от того, какое частное решение x ^чн мы выберем). Если (8) расписать покоординатно, получим решение (3). Векторная форма дает хорошее геометрическое представление о множестве решений.

2. Примеры.

Пример 1. Рассмотрим систему

Расширенная матрица имеет вид:

.

Вычитая из 2-й строки 1-ю, умноженную на 2, получаем ступенчатый вид этой матрицы

,

.

Следовательно, система совместна: х ₁, х ₂ – зависимые переменные, х ₃, х ₄ – свободные.

Новая система имеет вид:

Переносим члены со свободными переменными вправо:

Закончился прямой ход метода Гаусса. Теперь – обратный ход. Из последнего уравнения получаем

.

Подставляем в первое:

откуда

.

Итак,

(*)

– общее решение в координатной форме неоднородной системы.

Найдем векторную форму. Для этого в (*) заменим свободные члены нулями:

1) Пусть ,

.

2) Пусть ,

.

Следовательно,

.

Найдем частное решение неоднородной системы. Полагая в (*) , получаем: .

Следовательно,

.

Итак,

– общее решение в векторной форме.

Пример 2.

Расширенная матрица имеет вид:

система несовместна.

Это и понятно: последнее уравнение в новой системе имеет вид:

– решений нет.

Пример 3.

Расширенная матрица:

Свободных переменных нет. Решение единственно:

.

Лекция 11.

Тема: Действия на матрицами

1. Сложение матриц, умножение на число.

Эти операции над матрицами, как и над векторами, выполняются покоординатно.

Если

– матрицы одного порядка , то их сумма есть матрица того же порядка

с коэффициентами

.

Аналогично, есть матрица с коэффициентами .

Роль нуля при сложении играет нулевая матрица

2. Произведение матриц.

Пусть А – матрица порядка , В – матрица порядка . Определим матрицу

порядка .

Пусть

Коэффициент c_ij матрицы С (расположенный в i-й строке и j-м столбце) равен скалярному произведению i-й строки матрицы А на j-й столбец матрицы В:

.

Таким образом,

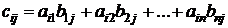
или

.

Далее мы будем рассматривать квадратные матрицы.

Пусть матрицы А и В – квадратные порядка n. Тогда можно вычислить два произведения: АВ и ВА. Оказывается, что они могут быть различны! Приведем

Пример. Положим

.

Тогда

,

Рассмотрим другой

Пример. Пусть

.

При умножении произвольного вектора на матрицу А слева вектор поворачивается против часовой стрелки на угол , сохраняя длину:

(Проверьте это для векторов е₁ = (1, 0) и е₂ = (0, 1)).

Докажите, что

Таким образом, матрицы и всегда коммутируют (перестановочны), то есть .

Роль единицы при умножении квадратных матриц играет единичная матрица:

,

на главной диагонали которой стоят единицы, а остальные коэффициенты – нули.

Единичная матрица обладает также тем свойством, что

.

3. Обратная матрица.

Пусть А и В – квадратные матрицы порядка n.

Определение. Матрица В называется обратной к матрице А, если

.

Для обратной матрицы В используют обозначение А ^-1 – обратная к А.

Далеко не всякая матрица имеет обратную.

Теорема. Матрица А имеет обратную тогда и только тогда, когда .

Отметим, что строки матрицы А линейно независимы 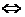столбцы матрицы А линейно независимы .

Матрица, у которой определитель не равен нулю, то есть существует обратная, называется невырожденной.

Пример. Пусть снова

.

Тогда матрица поворота на угол – является обратной к . Действительно,

.

Как вычислить обратную матрицу в общем случае? Есть два способа. Опишем их.

Пусть – невырожденная матрица.

Первый способ.

1) Для каждого элемента а_ij вычислим алгебраическое дополнение

,

где – минор элемента а_ij, то есть определитель матрицы, полученной из А вычеркиванием i-той строки и j-го столбца.

Составим из алгебраических дополнений матрицу

.

2) Транспортируем матрицу :

,

то есть сделаем 1-ый столбец 1-ой строкой,..., последний столбец – последней строкой. Матрицу назовем присоединенной к матрице А.

3) Разделим полученную матрицу на определитель матрицы А.

Получилась обратная матрица:

. (1)

Пример. Пусть , матрица А невырожденная, то есть обратная матрица существует.

1) А ₁₁ = 4 А ₁₂= –3

А ₂₁ = –2 А ₂₂= 1

.

2) .

3) .

Второй способ.

К матрице А справа припишем единичную матрицу Е. Получим прямоугольную матрицу порядка :

.

С помощью элементарных преобразований (перестановок строк, умножения или деления строки на число, прибавления к одной строке другой, умноженной на число) добьемся того, чтобы на месте матрицы А оказалась бы единичная матрица Е. Тогда на месте единичной окажется обратная:

.

Подчеркнем, что преобразования производятся над строками длины 2 п, то есть преобразуется целиком вся матрица (). Для невырожденной матрицы А такое преобразование всегда возможно.

Пример. Рассмотрим снова матрицу

.

Найдем обратную:

.

Мы получили тот же ответ, что и при использовании первого
способа.

Проверьте (как?), что – обратная матрица.

4. Использование обратной матрицы для решения линейных систем.

Пусть дана система уравнений с п неизвестными:

с невырожденной матрицей

, то есть .

Запишем систему в матрично-векторном виде:

. (2)

где – неизвестный вектор и правая часть системы соответственно. Умножим (2) на А ^-1 слева:

.

Поскольку

,

то

(3)

– решение системы. Оказывается, что если (3) расписать покоординатно, то мы получим знакомые вам формулы Крамера:

.

Постарайтесь понять, почему это так, воспользовавшись представлением для (3):

.

Пример. Решить пару систем

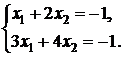
Обе системы имеют одну и ту же матрицу , обратная к которой нам известна: .

В первом случае , во втором .

Воспользуемся формулой (3):

– решение первой системы,

– решение второй.

Тема: Применения линейной алгебры в экономике

1. Модель “затраты – выпуск”.

Имеется предприятие, выпускающее п видов продукции в количествах х ₁, х ₂,..., х_п соответственно.

Вектор называется планом выпуска.

При этом расходуется т видов ресурсов, имеющихся в количествах b ₁, b ₂,..., b_m соответственно.

Вектор называется вектором ресурсов.

Известны расходные коэффициенты a_ij – количество i-го ресурса, необходимого для производства единицы j-го продукта, i = 1,..., m, j = 1,..., n.

Они образуют матрицу

,

которую называют матрицей расходных коэффициентов, или технологической матрицей. При плане х = (х ₁,..., х_п) расход i-го ресурса составит величину

,

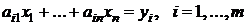(почему?) или в матричной форме

,

где у – вектор расходов ресурсов.

Можно рассматривать модель, когда расходы не превышают
запасы:

,

то есть

,

где неравенства между векторами понимаются покомпонентно. А можно потребовать, чтобы расходовались все имеющиеся ресурсы.

Тогда

,

то есть

.

Рассмотрим последний вариант. Пусть даны запасы ресурсов b и, конечно, матрица расходных коэффициентов А. Требуется определить план выпуска такой, что

.

Это означает, что надо найти решение линейной системы.

Если т = п и , то решение дается формулой

Не нашли, что искали? Воспользуйтесь поиском: