
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Замкнені множини. Ізольовані, граничні, межові точки множин
Практикум з курсу
„Топологія”
Редактор А.Я. Пащенко
Техредактор Л.П. Замятіна
Коректор Т.А. Белиба
Підписано до друку.05.2013. Формат 60x84/16. Папір друкарський.
Друк плоский. Ум.друк.арк.. Ум.фарбовідб.. Обл.-вид.арк..
Тираж 100 пр. Зам. №.
РВВ ДНУ, пр. Гагаріна, 72, м. Дніпропетровськ, 49010.
Друкарня ДНУ, вул. Наукова, 5, м. Дніпропетровськ, 49050.
© Тушев А.В., Турбай Н.А., 2013
Метричні й топологічні простори
Варіант 1
1. Довести, що множина всіх неперервних на 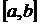 функцій складає метричний простір, якщо під відстанню між двома елементами
функцій складає метричний простір, якщо під відстанню між двома елементами  та
та  цієї множини розуміти число
цієї множини розуміти число
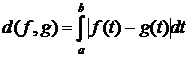 .
.
2. Нехай 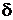 і
і 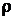 - дві метрики на множині
- дві метрики на множині  . Довести, що якщо існують сталі
. Довести, що якщо існують сталі 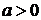 та
та 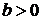 такі, що
такі, що
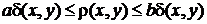 ,
, 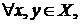
то метрики 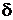 та
та 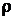 еквівалентні.
еквівалентні.
3. Нехай 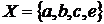 . Визначити, які з наступних наборів його підмножин є топологічними структурами на множині
. Визначити, які з наступних наборів його підмножин є топологічними структурами на множині  :
:
а)  ,
, 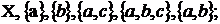
б)  ,
, 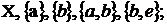
в)  ,
, 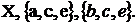
Якщо який-небудь з наборів а) – в) виявиться топологією, то знайти сім’ю замкнених множин для цих топологій.
4. Довести, що 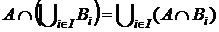 .
.
Варіант 2
1. Визначити, чи є метричним простором множина всіх дійсних чисел, якщо під відстанню між двома числами  та
та 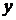 розуміти число
розуміти число
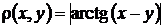
2. Довести, що метрики 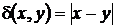 і
і 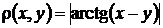 , задані на множині
, задані на множині  , еквівалентні.
, еквівалентні.
3. Нехай  – промінь
– промінь  , а
, а  складається з
складається з  ,
,  і всіх можливих променів
і всіх можливих променів  , де
, де 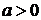 . Визначити, чи є
. Визначити, чи є  топологією на
топологією на  . Якщо так, знайти сім’ю замкнених множин.
. Якщо так, знайти сім’ю замкнених множин.
4. Довести, що 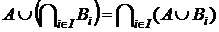 .
.
Варіант 3
1. Визначити, чи буде метричним простором множина дійсних чисел, якщо метрику 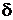 на ній означити так:
на ній означити так:
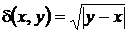 .
.
2. Довести, що метрики 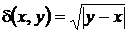 і
і  – еквівалентні на множині
– еквівалентні на множині  .
.
3. Нехай  – числова пряма,
– числова пряма,  складається з
складається з  ,
,  і всіх можливих променів вигляду
і всіх можливих променів вигляду 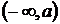 , де
, де 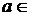
 . Визначити, чи буде
. Визначити, чи буде  топологією на
топологією на  . Якщо так, знайти сім’ю замкнених множин.
. Якщо так, знайти сім’ю замкнених множин.
4. Довести, що 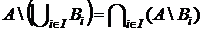 .
.
Варіант 4
1. Довести, що функція 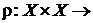
 + (
+ ( +– множина невід’ємних дійсних чисел) є метрикою на
+– множина невід’ємних дійсних чисел) є метрикою на  тоді і тільки тоді, коли виконуються такі умови:
тоді і тільки тоді, коли виконуються такі умови:
а) 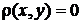
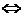
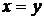 ;
;
б) 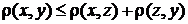 ,
, 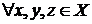 .
.
2. Довести, що метрики 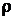 і
і 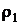 еквівалентні на множині.
еквівалентні на множині.
3. Нехай  – нескінченна множина, а
– нескінченна множина, а  – топологія скінчених доповнень на
– топологія скінчених доповнень на  . Довести аксіоми відкритих множин. Знайти сім’ю замкнених множин.
. Довести аксіоми відкритих множин. Знайти сім’ю замкнених множин.
4. Довести, що 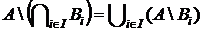 .
.
Варіант 5
1. Довести, що функція 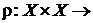
 + (
+ ( +– множина невід’ємних дійсних чисел) є функцією, яка задовольняє умовам:
+– множина невід’ємних дійсних чисел) є функцією, яка задовольняє умовам:
а) 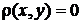
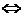
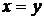 ;
;
б) 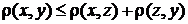 ,
, 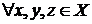
то функція 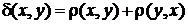 буде метрикою на
буде метрикою на  .
.
2. Довести, що метрики 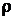 і
і 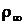 еквівалентні на множині.
еквівалентні на множині.
3. Визначити, чи буде перетин топологій, які задані на одній і тій самій множині  , топологією на
, топологією на  .
.
4. Довести, що 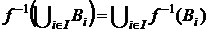 ,
,  – відображення і
– відображення і  .
.
Варіант 6
1. Довести, що якщо 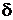 і
і 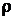 – метрики на
– метрики на  , то
, то  і
і 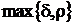 також є метриками на
також є метриками на  . Чи будуть метриками функції
. Чи будуть метриками функції  ;
; 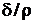 ;
; 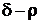 ?
?
2. Довести, що метрики 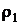 і
і 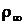 еквівалентні на множині
еквівалентні на множині  .
.
3. Визначити, чи буде об’єднання топологій, які задані на одній і тій самій множині  , топологією на
, топологією на  .
.
4. Довести, що 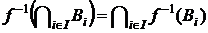 ,
,  – відображення і
– відображення і  .
.
Варіант 7
1. Довести, що коли 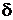 – метрика на
– метрика на  , то функція
, то функція 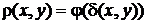 також є метрикою, якщо
також є метрикою, якщо 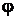 задовольняє умовам
задовольняє умовам 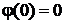 , монотонно зростає і
, монотонно зростає і
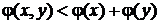 ,
, 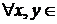
 .
.
2. Показати, що метрики 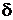 і
і 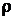 (див. задачу 1) еквівалентні, якщо
(див. задачу 1) еквівалентні, якщо 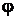 – неперервна функція.
– неперервна функція.
3. Нехай  – площина. Визначити, чи буде топологічною структурою набір множин, що складається з
– площина. Визначити, чи буде топологічною структурою набір множин, що складається з  ,
,  і відкритих кругів з центром в одній і тій самій точці з різноманітними радіусами.
і відкритих кругів з центром в одній і тій самій точці з різноманітними радіусами.
4. Довести, що 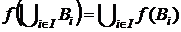 ,
,  – відображення і
– відображення і 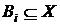 .
.
Варіант 8
1. Нехай 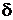 – метрика на
– метрика на  . Довести, що функція
. Довести, що функція 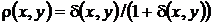 також є метрикою.
також є метрикою.
2. Довести, що метрики 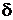 і
і 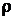 (див. задачу 1) еквівалентні.
(див. задачу 1) еквівалентні.
3. Нехай 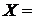
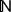 і
і 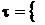
 ,
, 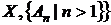 , де
, де 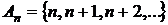 . Визначити, чи буде
. Визначити, чи буде  топологією на множині
топологією на множині 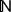 . Якщо так, то навести опис сім’ї замкнених множин.
. Якщо так, то навести опис сім’ї замкнених множин.
4. Довести, що 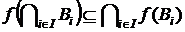 ,
,  – відображення і
– відображення і 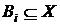 .
.
Варіант 9
1. Нехай 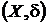 – метричний простір і
– метричний простір і 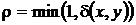 . Довести, що
. Довести, що 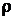 – метрика на
– метрика на  .
.
2. Довести, що метрики 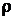 та
та 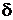 з задачі 1 еквівалентні.
з задачі 1 еквівалентні.
3. Знайти число різних топологій на множині з трьох елементів. Навести опис сім’ї замкнених множин цих топологій.
4. Навести приклад, коли 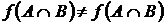 , де
, де  – відображення і
– відображення і 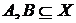 .
.
Замкнені множини. Ізольовані, граничні, межові точки множин
Варіант 1
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин, що належать 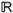 :
:
а) 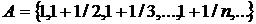 ;
;
б) 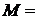
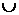
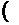 (
( \
\ 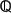 )
) 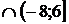
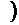 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множин усіх точок вигляду 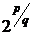 , де
, де 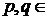
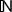 .
.
3. Навести опис топологічної структури, замкнених множин і околи точок, що індукуються в множині 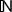 топологією прямої
топологією прямої  .
.
4. Нехай множина  відкрита в топологічному просторі
відкрита в топологічному просторі  і
і 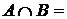
 , де
, де 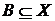 . Довести, що
. Довести, що 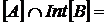
 .
.
5. Нехай 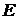 – підмножина метричного простору. Відомо, що
– підмножина метричного простору. Відомо, що 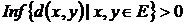 . Довести, що
. Довести, що 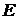 не має граничних точок.
не має граничних точок.
Варіант 2
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 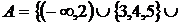 (
(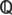
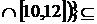
 ; б)
; б) 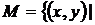
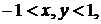 де
де 
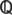
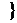 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множини всіх точок вигляду 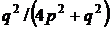 , де
, де 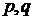 – усі можливі цілі числа, відмінні від нуля.
– усі можливі цілі числа, відмінні від нуля.
3. Описати топологічну структуру 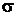 , що індукована в
, що індукована в 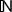 топологією стрілки. (простір із задачі 3 варіанта 2 лабораторної роботи 1 називається стрілкою). Описати в топологічному просторі (
топологією стрілки. (простір із задачі 3 варіанта 2 лабораторної роботи 1 називається стрілкою). Описати в топологічному просторі (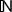 ,
, 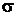 ) сім’ю замкнених множин околів точки.
) сім’ю замкнених множин околів точки.
4. Нехай множина  – замкнена, а множина
– замкнена, а множина  – відкрита. Довести, що
– відкрита. Довести, що 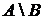 – замкнена,
– замкнена, 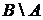 – відкрита.
– відкрита.
5. Нехай 
 – множина вигляду
– множина вигляду  , де
, де 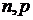 пробігають усі натуральні числа. Визначити, чи буде множина
пробігають усі натуральні числа. Визначити, чи буде множина 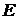 замкненою. Яка у неї похідна множина? Якими будуть друга та третя похідні множини?
замкненою. Яка у неї похідна множина? Якими будуть друга та третя похідні множини?
Варіант 3
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 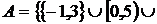 (
(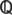
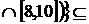
 ;
;
б) 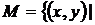
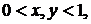 де
де 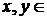
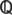
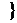 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множини всіх точок вигляду 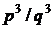 , де
, де 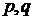 пробігають цілі числа
пробігають цілі числа 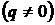 .
.
3. Описати топологічну структуру, що є індукованою у множині цілих чисел  топологією множини дійсних чисел із задачі 3 варіант 1 лабораторної роботи 1. Описати замкнені множини та сім’ю околів точки в
топологією множини дійсних чисел із задачі 3 варіант 1 лабораторної роботи 1. Описати замкнені множини та сім’ю околів точки в  .
.
4. Визначити, чи справді для будь-яких множин  і
і  топологічного простору виконуються рівності
топологічного простору виконуються рівності 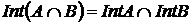 ;
; 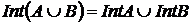 .
.
5. Нехай метрика 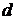 на множині
на множині  задовольняє такі умови
задовольняє такі умови
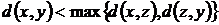 ,
, 
 .
.
Довести, що у метричному просторі  сфери не тільки замкнені, а ще й відкриті.
сфери не тільки замкнені, а ще й відкриті.
Варіант 4
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 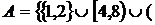 (
( \
\ 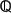 )
) 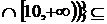
 ; б)
; б) 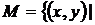
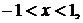
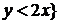 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множини всіх точок вигляду 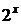 , де
, де 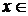
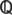 .
.
3. Навести опис топологічної структури 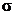 , що є індукованою на множині
, що є індукованою на множині 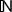 топологією скінчених доповнень у множині дійсних чисел. Навести опис замкнених множин та околи точок в просторі (
топологією скінчених доповнень у множині дійсних чисел. Навести опис замкнених множин та околи точок в просторі (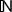 ,
, 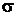 ).
).
4. Довести, що якщо множини  і
і  топологічного простору задовольняють умові
топологічного простору задовольняють умові 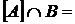

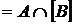 , то
, то 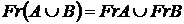 .
.
5. Довести, що множина  метричного простору
метричного простору  обмежена тоді і тільки тоді, коли вона міститься у деякій кулі. Як пов’язані між собою радіус цієї кулі і
обмежена тоді і тільки тоді, коли вона міститься у деякій кулі. Як пов’язані між собою радіус цієї кулі і 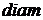
 ?
?
Варіант 5
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 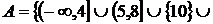 (
(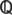
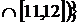 ;
;
б) 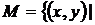
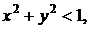
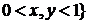 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множини всіх точок вигляду 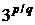 , де
, де 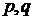 пробігають від’ємні цілі числа.
пробігають від’ємні цілі числа.
3. Довести, що топологія числової прямої  і топологія що індукована на множині дійсних чисел за допомогою топології площини (топології
і топологія що індукована на множині дійсних чисел за допомогою топології площини (топології  2), збігаються. Довести, що єдиною відкритою множиною прямої, яка також відкрита на площині, є
2), збігаються. Довести, що єдиною відкритою множиною прямої, яка також відкрита на площині, є  .
.
4. Довести, що відкрита множина  тоді і тільки тоді перетинається з множиною
тоді і тільки тоді перетинається з множиною  , коли
, коли 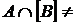
 (
( і
і  – підмножини топологічного простору).
– підмножини топологічного простору).
5. Навести приклад двох неперетинних замкнених множин на прямій, відстань між якими дорівнює нулю.
Варіант 6
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 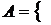
 \
\ 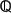
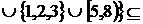
 ;
;
б) 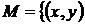 |
| 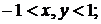
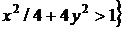 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання множини всіх точок вигляду 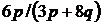 , де
, де 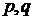 – натуральні числа.
– натуральні числа.
3. Довести, що множина 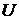 відкрита в топологічному просторі
відкрита в топологічному просторі  тоді і тільки тоді, коли кожна точка множини
тоді і тільки тоді, коли кожна точка множини 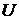 має в
має в  такий окіл
такий окіл 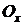 , що
, що 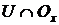 відкритий в
відкритий в 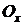 .
.
4. Довести, що для будь-яких неперетинних відкритих множин топологічного простору замикання одного з них не перетинається з іншим.
5. Нехай  – нескінченна множина, яка має топологією скінчених доповнень. Перевірити аксіоми відкритих множин і довести, що кожна точка
– нескінченна множина, яка має топологією скінчених доповнень. Перевірити аксіоми відкритих множин і довести, що кожна точка 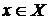 є граничною для будь-якої нескінченої підмножини
є граничною для будь-якої нескінченої підмножини  .
.
Варіант 7
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 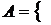
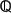
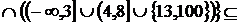
 ;
;
б) 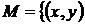 |
| 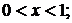
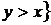 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання всіх точок вигляду 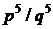 , де
, де 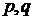 – всілякі невід’ємні цілі числа.
– всілякі невід’ємні цілі числа.
3. Нехай  – підпростір топологічного простору
– підпростір топологічного простору  і
і 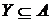 . Нехай також
. Нехай також 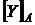 – замикання
– замикання  у підпросторі
у підпросторі  ,
, 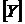 – замикання
– замикання  у просторі
у просторі  . Показати, що
. Показати, що 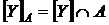 .
.
4. Довести, що коли  – замкнена множина топологічного простору, то
– замкнена множина топологічного простору, то 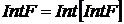 .
.
5. Нехай  і
і  – довільні підмножини топологічного простору. Довести, що
– довільні підмножини топологічного простору. Довести, що 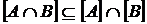 . Навести приклад, коли ці множини не збігаються.
. Навести приклад, коли ці множини не збігаються.
Варіант 8
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 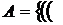
 \
\ 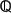 )
) 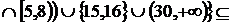
 ;
;
б) 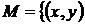 |
| 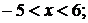
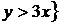 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання всіх точок вигляду 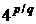 , де
, де 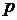 – від’ємне ціле число, а
– від’ємне ціле число, а 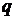 – натуральне.
– натуральне.
3. Нехай 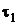 і
і 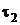 - топології на
- топології на  такі, що
такі, що 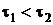 . Нехай далі
. Нехай далі 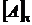 – замикання множини
– замикання множини  відносно
відносно  . Довести, що
. Довести, що 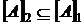 для
для 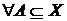 .
.
4. Довести, що 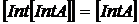 для будь-якої множини
для будь-якої множини  топологічного простору
топологічного простору  .
.
5. Довести, що підмножина 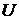 метричного простору
метричного простору  відкрита тоді і тільки тоді, коли
відкрита тоді і тільки тоді, коли 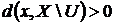 для
для 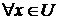 .
.
6.
Варіант 9
1. Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а) 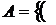
 \
\ 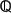 )
) 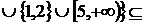
 ;
;
б) 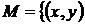 |
| 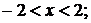
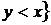 .
.
Ці множини є відкритими чи замкненими?
2. Знайти замикання всіх точок вигляду 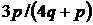 , де
, де 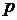 – від’ємне ціле число, а
– від’ємне ціле число, а 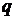 – натуральне.
– натуральне.
3. Нехай  – підпростір топологічного простору
– підпростір топологічного простору  і
і 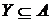 . Нехай також
. Нехай також 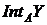 – внутрішність
– внутрішність  в
в  ,
, 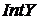 – внутрішність
– внутрішність  в
в  . Чи вірно, що
. Чи вірно, що 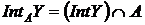 ?
?
4. Довести, що ізольована точка  множини
множини  топологічного простору
топологічного простору  належить
належить 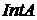 тоді й тільки тоді, коли множина
тоді й тільки тоді, коли множина  відкрита в
відкрита в  . У противному разі точка
. У противному разі точка  є межовою точкою
є межовою точкою  .
.
5. Визначити, чи дійсно 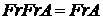 . Чи буде
. Чи буде 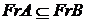 , якщо
, якщо 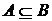 ?
?
Не нашли, что искали? Воспользуйтесь поиском: