Скрізь щільні та ніде не щільні множини.

Сепарабельні простори. Неперервні відображення

Варіант 1

1. Довести, що підмножина топологічного простору ніде не щільна тоді і тільки тоді, коли .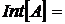

2. Довести, що для будь-якої відкритої підмножини 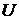в топологічному просторі множина ніде не щільна.

3. Довести, що в сепарабельному топологічному просторі множина всіх ізольованих точок є зчисленною (нескінченною або скінченною).

4. Довести, що топологічний простір є дискретний тоді і тільки тоді, коли кожне його відображення у топологічний простор неперервне.

Варіант 2

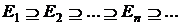1. Навести приклад послідовності скрізь щільних множин на прямій, таких, що , а також .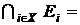

2. Довести, що топологічний простір буде дискретним тоді і тільки тоді, коли скрізь щільною множиною в ньому буде тільки він самий. Подати прямий опис скрізь щільних множин у топології стрілки.

3. Довести, що в сепарабельному топологічному просторі будь-яка сім'я не порожніх відкритих неперетинних множин буде зчисленною (нескінченною або скінченною).

4. Довести, що відображення топологічних просторів та неперервне тоді і тільки тоді, коли для кожного елемента деякої бази β простору є відкрита множина в .

Варіант 3

1. Довести, що множина топологічного простору ніде не щільна в тоді і тільки тоді, коли в будь-якій не порожній відкритій множині 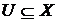існує така не порожня відкрита підмножина 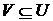, що .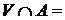

2. Довести, що межа замкненої множини ніде не щільна.

3. Довести, що топологічний добуток скінченної кількості сепарабельних просторів – сепарабельний.

4. Довести, що відображення топологічних просторів та неперервне тоді і тільки тоді, коли для кожної множини .

Варіант 4

1. Довести, що множина топологічного простору скрізь щільна в тоді і тільки тоді, коли для будь-якої не порожньої відкритої підмножини .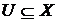

2. Нехай і – скрізь щільні підмножини топологічного простору і – відкрита в . Довести, що 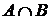є скрізь щільна множина в .

3. Довести, що будь-який підпростір сепарабельного метризованого простору – сепарабельний.

4. Визначити, чи буде замкнене відображення одного топологічного простору на інший також відкритим.

Варіант 5

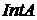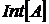1. Множина – ніде не щільна в топологічному просторі . Що можна сказати про , і ?

2. Навести прямий опис множин скрізь щільних у тривіальному просторі та в просторі скінченний доповнень.

3. Довести, що цілком обмежений метричний простір є сепарабельним.

4. Визначити, чи буде відкрите відображення одного топологічного простору на інший також замкненим.

Варіант 6

1. Довести, що підмножина топологічного простору ніде не щільна в тоді і тільки тоді, коли в будь-якій не порожній відкритій множині 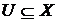існує така не порожня відкрита множина 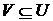, що .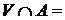

2. Довести, що об’єднання скінченного числа ніде не щільних в просторі множин ніде не щільне в .

3. Довести, що образ сепарабельного простору при неперервному відображенні буде сепарабельним.

4. Довести, що відображення топологічних просторів та замкнене тоді і тільки тоді, коли для будь-якої підмножини .

Варіант 7

1. Довести, що підмножина топологічного простору скрізь щільна в тоді і тільки тоді, коли для будь-якої не порожньої відкритої підмножини .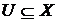

2. Довести, що перетин скінченного числа відкритих скрізь щільних у просторі множин буде скрізь щільним в .

3. Нехай – неперервне сюр’єктивне відображення топологічних просторів та – сепарабельним топологічний простір. Довести, що простір – сепарабельний.

4. Довести, що відображення топологічних просторів та відкрите тоді і тільки тоді, коли для кожного елемента деякої бази β простору є відкрита множина в .

Варіант 8

1. Довести, що підмножина топологічного простору ніде не щільна в тоді і тільки тоді, коли в будь-якій не порожній відкритій множині 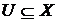існує така не порожня відкрита множина 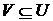, що .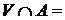

2. Нехай – ніде не щільна в топологічному просторі та 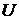– довільна відкрита в множина. Довести, що множина 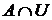ніде не щільна в 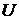( 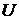розглядається як підпростір ).

3. Довести, що якщо в топологічному просторі є така зчисленна сім’я не порожніх відкритих множин, що будь-яка не порожня відкрита множина містить елемент (хоч один) цієї сім’ї, то будь-який скрізь щільний в підпростір буде сепарабельним.

4. Довести, що відображення топологічних просторів та відкрите тоді і тільки тоді, коли для будь-якої підмножини .

Варіант 9

1. Довести, що множина ніде не щільна тоді і тільки тоді, коли в будь-якому околі будь-якої точки існує точка, що входить разом з деяким своїм околом в доповнення множини .

2. Навести прямий опис множин скрізь щільних у дискретному просторі та в топології стрілки.

3. Довести, що якщо простір з першою аксіомою зчисленності буде сепарабельним, то і будь-який скрізь щільний в підпростір теж сепарабельний.

4. Навести приклад негомеоморфних топологічних просторів, кожний з яких гомеоморфний підпростору іншого.

Не нашли, что искали? Воспользуйтесь поиском: