Компактні топологічні простори

Варіант 1

1. Довести, що в кожному нескінченному компактному просторі існує зчисленна незамкнена множина.

2. Довести, що перетин будь-якої сім’ї компактних підмножин гаусдорфового простору буде компактним.

3. Довести, що якщо 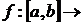- неперервна функція, то – замкнений інтервал або точка.

Варіант 2

1. Нехай – нескінченна множина, яка наділена топологією скінченних доповнень. Довести, що будь-яка підмножина цього простору буде компактною.

2. Довести, що перетин спадної послідовності компактних не порожніх зв’язних підмножин гаусдорфового простору також буде не порожньою зв’язною множиною.

3. Нехай – метричний простір, а – його компактний підпростір. Довести, що для існує , такий що .

Варіант 3

1. Довести, що якщо – замкнена множина, а – неперетинна з ним компактна підмножина метричного простору, то .

2. Нехай 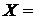, де – множина дійсних чисел, а . Введемо на множині топологію, у якій відкритими множинами будуть об’єднання відкритих множин, які належать з множиною . Перевірити аксіоми відкритих множин. Довести, що множина – компактна, а – не компактна.

3. З’ясувати, які з наведених множин будуть компактними:

а) 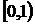в ;

б) ⁺= | в ;

в) коло в ²;

г) куля в ²;

д) однополий гіперболоїд в ³.

Варіант 4

1. Нехай і – компактні підмножини метричного простору. Довести, що існують такі точки і , що .

2. Довести, що замкнена підмножина фінально-компактного простору буде фінально-компактною

3. Довести, що графік функції 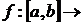компактний у ² тоді і тільки тоді, коли – неперервна функція.

Варіант 5

1. Нехай – довільна не порожня множина, а – компактна підмножина метричного простору. Довести, що існує така точка , що .

2. Довести, що компактний гаусдорфів простір метризований тоді, коли він має зчисленну базу.

3. Навести приклад розривної функції 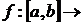, графік якої замкнений, але некомпактний.

Варіант 6

1. Довести, що перетин будь-якої сім’ї замкнених компактних множин буде компактною множиною.

2. Нехай – топологічний простір, а – компактний топологічний простір. Довести, що відображення 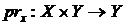буде замкненим неперервним відображенням.

3. Довести, що властивість зчисленної компактності спадкується при переході до замкненого підпростору.

Варіант 7

1. Довести, що компактний простір з дискретною топологією – скінченний.

2. Довести, що топологічний простір компактний тоді і тільки тоді, коли кожне покриття цього простору елементами деякої бази містить скінченне під покриття.

3. Довести, що неперервний образ зчисленно-компактної множини топологічного простору також зчисленно-компактний.

Варіант 8

1. Довести, що неперервний образ фінально-компактної множини топологічного простору теж фінально-компактний.

2. Довести, що для будь-якої неперервної додатно-визначеної функції на компактному просторі існує таке, що для .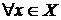

3. З’ясувати, чи будуть компактними дискретні та тривіальні топологічні простори.

Варіант 9

1. Нехай для 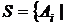– довільна сім’я компактних підмножин у гаусдорфовому просторі така, що перетин будь-якого скінченного числа елементів з – зв’язний. Довести, що множина – зв’язна.

2. Довести, що будь-який простір компактного метризованого простору – сепарабельним.

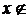
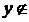
3. Нехай , де – множина дійсних чисел, , , . Введемо в топологію, у якій множина відкрита тоді і тільки тоді, коли вона або відкрита в , або доповнення до неї скінченне. Перевірити аксіоми відкритих множин. Довести, що множини і – компактні в але їх перетин – не компактний.

Список рекомендованої літератури

Александров, А.Д. Геометрия [Текст] / А.Д. Александров, И.Ю. Нецветаев. – М.: Наука, 1990. – 672 с.

Александрян, Р.А. Общая топология [Текст] / Р.А. Александрян,
Є.А. Мирзаханян. – М: Высш. шк., 1979. – 336 с.

Борисенко, О.А. Диференціальна геометрія і топологія [Текст] /
О.А. Борисенко. – Х.: Основа, 1995. – 304 с.

Введение в топологию [Текст] / Ю.Г. Барисович, Н.М. Близняков,
Я.А. Израилевич, Т.Н. Фоменко. – М.: Высш. Шк., 1980. – 295 с.

Денисов, А. А. Дифференциальная геометрия и топология [Текст]: в 2 ч. / А.А. Денисов. – Днепропетровск: Изд-во ДГУ, 1993. – Ч. 1. – 76 с.

Колмогоров, А.Н. Элементы теории функций и функционального анализа [Текст] / А.Н. Колмогоров, С.В. Фомин. – М.: Наука, 1989. – 624 с.

Косневски, Ч. Начальный курс алгебраической топологии [Текст] /Ч. Косневски. – М.:Мир, 1983. – 304 с.

Мищенко, А.С. Курс дифференциальной геометрии и топологии [Текст] / А.С. Мищенко, А.Т. Фоменко. – М.: Изд-во МГУ, 1980. – 439 с.

Федорчук, В.В. Общая топология. Основные конструкции [Текст] / В.В.Федорчук, В.В. Филипов. – М.: Изд-во МГУ, 1988. – 252 с.

Зміст

1. Метричні й топологічні простори………………………………………..3

2. Замкнені множини. Ізольовані, граничні, межові точки множин ……..5

3. Скрізь щільні та ніде не щільні множини.

Сепарабельні простори. Неперервні відображення …….....................9

4. Аксіоми зчисленності та відокремленості.

Нормальні простори. Гомеоморфні простори ………………………..11

5. Зв’язність топологічних просторів.

Лінійна зв’язність. Гомеоморфізм………………………………………14

6. Компактні топологічні простори……………………………………..…16

Список рекомендованої літератури…………………………………... 19

Не нашли, что искали? Воспользуйтесь поиском: