
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Аксіоми зчисленності та відокремленості.
Нормальні простори. Гомеоморфні простори
Варіант 1
1. Нехай  – простір з другою аксіомою зчисленності. Довести, що з будь-якої бази простору
– простір з другою аксіомою зчисленності. Довести, що з будь-якої бази простору  можна виділити зчисленний набір множин, який також буде базою простору
можна виділити зчисленний набір множин, який також буде базою простору  .
.
2. Навести приклад  – простору, який не є
– простору, який не є  – простором.
– простором.
3. Довести, що замкнений підпростір нормального простору також є нормальним.
4. Нехай  ,
,  – неперервні відображення
– неперервні відображення 
 . Довести, що підмножина простору
. Довести, що підмножина простору  , що складається з усіх розв’язків системи нерівностей
, що складається з усіх розв’язків системи нерівностей  ,
,  , буде відкритою. Чи можна скінченну систему замінити нескінченною?
, буде відкритою. Чи можна скінченну систему замінити нескінченною?
Варіант 2
1. Нехай  – множина дійсних чисел і β – сім’я всіх інтервалів типу
– множина дійсних чисел і β – сім’я всіх інтервалів типу  ,
,  . Довести, що сім’я β є базою деякої топології τ і що топологічний простір
. Довести, що сім’я β є базою деякої топології τ і що топологічний простір  – нормальний неметризований сепарабельний простір з першою аксіомою зчисленності, на якому не виконується друга аксіома зчисленності.
– нормальний неметризований сепарабельний простір з першою аксіомою зчисленності, на якому не виконується друга аксіома зчисленності.
2. Навести приклад негаусдорфового  – простору
– простору
3. Нехай  – гаусдорфів простір, у якому множина неізольованих точок скінченна. Довести, що
– гаусдорфів простір, у якому множина неізольованих точок скінченна. Довести, що  – нормальний простір.
– нормальний простір.
4. Побудувати гомеоморфізми між множинами:
а)  та
та 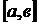 ,
,  ;
;
б) 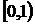 та
та  ;
;
в)  та
та  .
.
Варіант 3
1. Довести, що  – топологічний простір та вибрати в ньому дві різні бази, якщо:
– топологічний простір та вибрати в ньому дві різні бази, якщо:
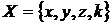 ,
,  ø,
ø,  .
.
2. Нехай  і
і  – дві різні топології на одній і тій самій множині
– дві різні топології на одній і тій самій множині  і
і  . Довести, що якщо
. Довести, що якщо  –
–  – простір (
– простір ( – простір), тоді
– простір), тоді  –
–  – простір (
– простір ( – простір).
– простір).
3. Довести, що регулярність є спадковою властивістю.
4. Довести, що простір  гомеоморфний до будь-якої відкритої кулі цього простору.
гомеоморфний до будь-якої відкритої кулі цього простору.
Варіант 4
1. Довести, що  – топологічний простір і вибрати мінімальну базу, якщо:
– топологічний простір і вибрати мінімальну базу, якщо:
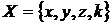 ,
,  ø,
ø,  .
.
2. Довести, що  – простір, у якому тільки одна точка не ізольована, а решта точок – ізольовані,- нормальний простір.
– простір, у якому тільки одна точка не ізольована, а решта точок – ізольовані,- нормальний простір.
3. Довести, що в  – просторі множина всіх граничних точок будь-якої підмножини замкнена.
– просторі множина всіх граничних точок будь-якої підмножини замкнена.
4. Нехай  і
і  – такі неперервні відображення топологічного простору
– такі неперервні відображення топологічного простору  в гаусдорфів простір
в гаусдорфів простір  , що множина
, що множина 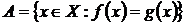 скрізь щільна в
скрізь щільна в  . Довести, що
. Довести, що  на всьому просторі
на всьому просторі  .
.
Варіант 5
1. Нехай β – база топологічного простору  і
і  . Довести, що сім’я
. Довести, що сім’я 
 де
де  утворює базу в підпросторі
утворює базу в підпросторі  .
.
2. Довести, що в  – просторі точка, база якої складається із скінченного числа елементів, ізольована.
– просторі точка, база якої складається із скінченного числа елементів, ізольована.
3. Довести, що в означенні регулярного простору аксіому  можна замінити на аксіому
можна замінити на аксіому  . Чи виконується це твердження для нормальних просторів?
. Чи виконується це твердження для нормальних просторів?
4. Нехай  ,
,  – неперервні відображення топологічного простору
– неперервні відображення топологічного простору  в
в  . Довести, що підмножина топологічного простору
. Довести, що підмножина топологічного простору  , яка складається із всіх розв’язків системи рівнянь
, яка складається із всіх розв’язків системи рівнянь 
 , буде замкненою. Чи можна скінченну систему рівнянь замінити нескінченною?
, буде замкненою. Чи можна скінченну систему рівнянь замінити нескінченною?
Варіант 6
1. Довести, що топологічний добуток скінченного числа топологічних просторів з другою аксіомою зчисленності буде топологічним простором з другою аксіомою зчисленності. Чи виконується обернене твердження?
2. Довести, що підмножина топологічного простору з першою аксіомою зчисленності замкнена тоді і тільки тоді, коли межа будь-якої збіжної в  послідовності з
послідовності з  належить
належить  .
.
3. Нехай  – множина дійсних чисел. Довести, що сім’я всіх інтервалів типу
– множина дійсних чисел. Довести, що сім’я всіх інтервалів типу  ,
,  буде базою деякої топології τ на множині
буде базою деякої топології τ на множині  . Довести, що
. Довести, що  – нормальний простір.
– нормальний простір.
4. Нехай  ,
,  – неперервні відображення топологічного простору
– неперервні відображення топологічного простору  в
в  . Довести, що підмножина топологічного простору
. Довести, що підмножина топологічного простору  , яка складається із всіх розв’язків системи рівнянь
, яка складається із всіх розв’язків системи рівнянь 
 , буде відкритою. Чи можна скінченну систему рівнянь замінити нескінченною?
, буде відкритою. Чи можна скінченну систему рівнянь замінити нескінченною?
Варіант 7
1. Довести, що будь-який підпростір простору з другою аксіомою зчисленності буде простором з другою аксіомою зчисленності.
2. Довести, що будь-який підпростір  – простору буде
– простору буде  – простором.
– простором.
3. Довести, що  – простір буде нормальним тоді і тільки тоді, коли для будь-яких двох замкнених неперетинних у ньому підмножин існує такий окіл однієї з них, що його замикання не перетинається з іншими.
– простір буде нормальним тоді і тільки тоді, коли для будь-яких двох замкнених неперетинних у ньому підмножин існує такий окіл однієї з них, що його замикання не перетинається з іншими.
4. Довести, що вся площина  2 гомеоморфна до будь-якого відкритого квадрату цієї площини.
2 гомеоморфна до будь-якого відкритого квадрату цієї площини.
Варіант 8
1. Навести приклад, який довів би, що неперервний образ простору з другою аксіомою зчисленності може не задовольняти цій аксіомі.
2. Довести, що у  – просторі будь-яка множина буде перетином деякої сім’ї відкритих множин.
– просторі будь-яка множина буде перетином деякої сім’ї відкритих множин.
3. Довести, що  – простір
– простір  тоді і тільки тоді регулярний, коли для будь-якої точки
тоді і тільки тоді регулярний, коли для будь-якої точки  та будь-якої замкненої множини
та будь-якої замкненої множини  , що не містить цю точку, існує такий окіл
, що не містить цю точку, існує такий окіл  , для якого
, для якого 
 .
.
4. Довести, що будь-який відкритий прямокутник в  2 буде гомеоморфний в
2 буде гомеоморфний в  2.
2.
Варіант 9
1. Довести, що образ бази при неперервних відображеннях може не бути базою.
2. Навести приклад  – простору, у якому ніяка множина з однією точкою не є замкненою.
– простору, у якому ніяка множина з однією точкою не є замкненою.
3. Довести, що образ нормального простору при неперервному замкненому відображенні буде нормальним простором.
4. Довести, що замкнений круг в  2 буде гомеоморфний до замкненого квадрату в
2 буде гомеоморфний до замкненого квадрату в  2.
2.
Не нашли, что искали? Воспользуйтесь поиском: