
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
4 страница. 12. Проверить, лежат ли в одной плоскости точки с координатами А(1; 1; 1),
12. Проверить, лежат ли в одной плоскости точки с координатами А(1; 1; 1),
B(2; 3; 1), C(3; 2; 1) и D(5; 9; 8).
13. В равнобедренном прямоугольном треугольнике даны координаты вершины
острого угла (1; -2) и уравнение противолежащего катета: 3x – 4y + 2 = 0.
Составить уравнения двух других сторон треугольника.
14. Написать уравнение плоскости, проходящей через точки А(-1; -2; 0) и
В(1; 1; 2) и перпендикулярный к плоскости x + 2y + 2z – 4 = 0.
15. Составить параметрические уравнения прямой, проходящей через точку
М(2; 3; -1) параллельно вектору 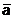 =(5; -3; 2).
=(5; -3; 2).
16. При каком значении коэффициента  плоскость
плоскость  x + 2y – z + 3 = 0
x + 2y – z + 3 = 0
параллельна прямой 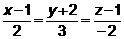 ?
?
ВАРИАНТ 28
1. 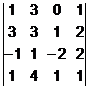 2.
2. 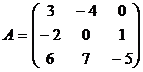 ,
,  ,
, 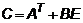
3. 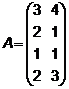 ,
, 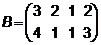 4.
4. 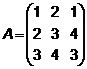 5.
5. 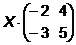 =
= 
6. 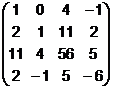 7.
7. 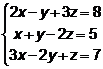 8.
8. 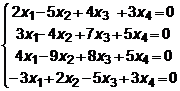
9.  ={11; -1; 4},
={11; -1; 4},  ={1; -1; 2},
={1; -1; 2}, 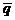 ={3; 2; 0} и
={3; 2; 0} и  {-1; 1; 1}.
{-1; 1; 1}.
10. Вычислить площадь треугольника АВС, если A(1; -2; 2), B(1; 4; 0) и
C(-4; 1; 1).
11. Найти угол между векторами  и
и  , если А(2; 3; 2), B(-1;-3;-1),
, если А(2; 3; 2), B(-1;-3;-1),
C(-3;-7;-3).
12. Найти объём параллелепипеда, построенного на векторах  ,
,  и
и  ,
,
если А(5; 2; 0), B(2; 5; 0), C(1; 2; 4) и D(-1; 1; 1).
13. Вершины треугольника А(2; 0), B(5; 3), C(3; 7). Найти уравнение прямой,
проходящей через вершину В и параллельной медиане АМ треугольника.
14. Написать уравнение плоскости, проходящей через точки  (1; -1; 2),
(1; -1; 2),
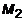 (2; 1; 2) и
(2; 1; 2) и  (1; 1; 4).
(1; 1; 4).
15. Написать уравнение прямой, проходящей через точку М(1; -1; 0) и
перпендикулярной к плоскости 2x – 4y + z = 3.
16. При каком значении  прямая
прямая 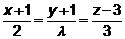 параллельна плоскости
параллельна плоскости
2x + y – z = 0?
ВАРИАНТ 29
1. 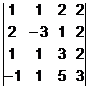 2.
2. 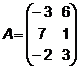 ,
,  ,
, 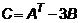
3. 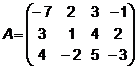 ,
, 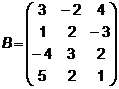 4.
4. 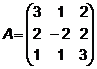
5. 

6.  7.
7.  8.
8. 
9.  ={-13; 2; 18},
={-13; 2; 18},  ={1; 1; 4},
={1; 1; 4}, 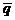 ={-3; 0; 2} и
={-3; 0; 2} и  {1; 2; -1}.
{1; 2; -1}.
10. Вычислить проекцию вектора 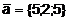 на ось вектора
на ось вектора  .
.
11. Найти орт 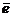 , перпендикулярный векторам
, перпендикулярный векторам 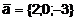 и
и  .
.
12. Проверить, лежат ли точки А(2; 3; 1), B(4; 1; -2), C(6; 3; 7) и D(7; 5; -3) в
одной плоскости.
13. Вершины треугольника А(0; 4), B(2; -3), C(-4; 5). Составить уравнение
высоты, опущенной из вершины С на медиану, проведенную из вершины А.
14. Написать уравнение плоскости, проходящей через точку М(1; 1; 1):
а) перпендикулярно и б) параллельно плоскости 2x + 4y + z – 5 = 0.
15. Найти угол между прямыми  и
и  .
.
16. Написать уравнение прямой, проходящей через точку М(2; 3; -1) и
перпендикулярной к плоскости 2x + 4y – 3z = 2.
ВАРИАНТ 30
1. 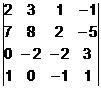 2.
2.  ,
, 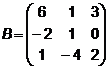 ,
, 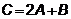
3.  ,
, 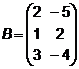 4.
4. 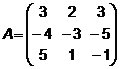
5. 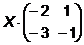 =
= 
6. 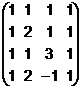 7.
7.  8.
8. 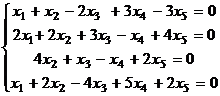
9.  ={0; -8; 9},
={0; -8; 9},  ={0; -2; 1},
={0; -2; 1}, 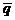 ={3; 1; -1} и
={3; 1; -1} и  {4; 0; 1}.
{4; 0; 1}.
10. Определить внешний угол при вершине А треугольника АВС, если
А(3; 2; -3), B(5; 1; -1) и C(1; -2; 1).
11. Вычислить площадь треугольника АВС, если А(1; -2; 2), B(-5; -5; 3),
C(-4; 1; 1).
12. Будут ли компланарны векторы  ,
,  и
и  ?
?
13. Вершины треугольника А(2; -1), B(4; 5), C(-3; 2). Написать уравнение
прямой, проходящей через начало координат и центр тяжести треугольника
АВС.
14. Составить уравнение плоскости, которая проходит через точку М(2; -1; 1)
перпендикулярно плоскостям 2x - y + 3z – 1 = 0 и x + 2y + z = 0.
15. Составить каноническое уравнение прямой  .
.
16. Написать уравнение плоскости, проходящей через точку М(2; -1; 3)
перпендикулярно прямой  .
.
Не нашли, что искали? Воспользуйтесь поиском: