Вимушені електричні коливання, змінний струм

Розглянемо тепер електричні коливання, які виникають при наявності в колі генератора ЕРС, яка періодично змінюється.

Коло з активним (омічним) опором. Спочатку розгля­немо частинний випадок, коли генератор змінного струму замк­нений на зовнішнє коло, яке,'містить лише активний опір (мал. 2.26). Припустимо, що в колі існує змінний струм:

Мал. 2.26.

Застосовуючи закон Ома, визначимо, за яким законом зміню­ється напруга на активному опорі

(2.72)

Мал. 2.27. Мал. 2.28.

Ця рівність показує, що між коливаннями та немає зсуву фаз: напруга і струм одночасно досягають макси­мальних значень і одночасно перетворюються в нуль (мал. 2.27). Наочно це можна зобразити за допомогою векторної діаграми. Величини, які змінюються за гармонічним зако­ном будемо розглядати як вектори, модуль яких дорівнює їхньому амплітудному значенню, а кут між ними - різниці фаз. Вісь діаграми виберемо так, щоб вектор I збігівся з нею за напрямком. Цю вісь називають віссю струмів. Тоді вектор, що зображає коливання напруги, бу­де направлений вздовж осі струмів (мал. 2.28). Довжина цього вектора

Коло з індуктивністю. Розглянемо випадок, коли ді­лянка кола містить лише індук­тивність (мал. 2.29). Тоді за зако­ном електромагнітної індукції Фарадея електрорушійна сила

(ЕРС) індукції визначається швидкістю зміни магнітного потоку тобто У випадку самоіндукції магнітний потік Ф прямо пропорційний силі струму що тече по контуру, тобто де - індуктивність контура.

Мал. 2.29.

Таким чином, при наявності змінного струму в котушці індукуєть­ся ЕРС самоіндукції, величина якої дорівнює Відповідно до закону Ома для повного кола сума всіх ЕРС за відсутності активного опору повинна дорівнювати нулю, тобто

Якщо сила струму в колі змінюється за законом 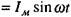, то для отримуємо:

(2.73)

Порівнюючи відношення для амплітудних значень І_т та U_m із законом Ома, бачимо, що роль опору відіграє величина яку називають індуктивним опором. Також видно, що сила струму та напруга зсунуті за фазою одна відносно іншої (мал. 2.30) на величину причому напруга в будь-який момент часу випереджає силу струму. На векторній діаграмі це зобразиться так, як пока­зано на мал. 2.31.

Мал. 2.30. Мал. 2.31.

Коло з ємністю. Розглянемо третій частинний випадок, коли ділянка кола містить лише конденсатор ємності С (мал. 2.32). Як і раніше, будемо вважати, що сила струму змінюється за законом Різниця потенціалів між пластинами конденсатора Але ж сила струму Тоді

(2.74)

Постійна інтегрування визначає заряд, який не пов'яза­ний з коливаннями струму, і тому можна покласти Отже,

(2.75)

де

Порівнюючи (2.75) із законом Ома, бачимо, що роль опору відіграє величина яка називається ємнісним опором. Ємнісний опір змен­шується із зростанням частоти. Бачимо також, що сила струму та напруга зсунуті по фазі на величи­ ну причому сила струму в будь-який момент часу виперед­жає напругу (мал. 2.33).

Мал. 2.32.

Отриманий результат зобразимо за допомогою вектор­ної діаграми (мал. 2.34). Вектор, що відповідає коливанням напруги, повернений у від'ємному напрямі (за годиннико­вою стрілкою) на кут Довжина вектора дорівнює амплі­туді напруги .

Мал. 2.33. Мал. 2.34.

Не нашли, что искали? Воспользуйтесь поиском: