Об'ємно-градієнтні ефекти в напівпровідниках

Наявність об'ємних домішкових неоднорідностей виявляється не тільки в їх впливі на усереднювання сигналу, що виміряється. Концентраційні градієнти (Ñ_n) або градієнти ПЕО (Ñ_r) приводять у присутності електричних і магнітних полів до виникнення безлічі різноманітних ерс, що спотворюють корисний сигнал вимірювальної інформації. П.І.Баранській, який вперше знайшов і детально дослідив ці ефекти, назвав їх об'ємно-градієнтними.

Ми вже відзначали, що неоднорідність будь-якого ступеня складності можна представити як суперпозицію східчастих елементарних n-n+ - або p-p+ -переходів.

Розглянемо напівпровідник з східчастою найпростішою неоднорідністю по r (рис.4.4)

При пропусканні струму густиною j в лівій частині зразка в одиницю часу в одиницю об'єму виділиться тепло, пропорційне j2r₁, а в правій частині - j2r₂. В загальному випадку температури лівої і правої частини зразка повинні бути нерівні (Т₁ 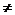Т₂), тобто між потенційними зондами виникає термоерс, яку називають ерс Джоуля–Зеебека:

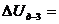a_1,2 (Т1 – Т2) (4.8)

де a_1,2 – коефіцієнт термоерс.

В неоднорідній структурі на її межі також повинне мати місце тепловиділення Пельтье:

Qп = pj (4.9)

де - коефіцієнт Пельтье .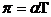

Повинен мати місце і третій базовий електротермічний ефект Томсона:

QТ=j (4.10)

де - коефіцієнт Томсона.

Таким чином, в міжзондовому просторі крім чисто омічного падіння напруги будуть присутні об'ємно-градієнтні термоерс Джоуля-Зєєбека, Пельтье і Томсона.

В більш загальному вигляді, для довільного градієнта Ñ_r можна отримати рішення кінетичного рівняння Больцмана в наближенні часу релаксації, прийнявши як збурюючий чинник координатну залежність рівня Фермі:

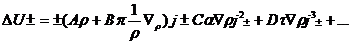(4.11)

де А, В, З, D, - якісь константи.

Аналіз отриманого виразу показує, що до омічного падіння напруги А 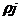додається безперервний затухаючий по величині ряд значень різних об'ємно-градієнтних ерс. Ми беремо до уваги тільки об'ємно-градієнтні ерс Джоуля – Зєєбека, Пельтье і Томсона. ЕРС Пельтье пропорційна першому ступеню j, тому її принципово неможливо відділити від корисного сигналу. Найсильнішим є Джоуль-Зєєбек – ефект, що вносить в кінцевий результат погрішність до 3 %. Його можна в значній мірі виключити усереднюванням результатів вимірювань при різних полярностях струму. Проте головним напрямом мінімізації паразитних об'ємно-градієнтних ерс є зменшення густини струму в розумних масштабах аж до межі чутливості методу.

Крім "стаціонарних об'ємно-градієнтних" ерс в неоднорідних зразках при пропусканні електричного струму може мати місце більш сильна об'ємно-градієнтна ерс із-за розподіленої (внутрішньої) інжекції,яку усунути важче. Фізична природа цієї ерс дуже проста – якщо є градієнт концентрації неосновних носіїв заряду n1 ¹ n2, то повинен мати місце і градієнт концентрації нерівноважних носіїв заряду, що витікає з умови

n1 p1 = n2 p2 = ni2 = const(T) (4.12)

В стаціонарному режимі при пропусканні струму між ділянками 1 і 2 виникає додаткова ерс розподіленої інжекції, викликана перетіканням нерівноважних носіїв заряду з однієї області в іншу.

Об'ємно-градієнтна ерс розподіленої інжекції тим більше, чим більше градієнт концентрацій і час життя нерівноважних носіїв заряду. Проте, на ці параметри важко вплинути, не змінюючи самої природи зразка, що виміряється. Тому залишається використовувати вже відомі нам прийоми зміни полярності і зменшення густини струму.

Об'ємно-градієнтні явища слід враховувати при особливо точних вимірюваннях ПЕО і ефекту Холу.

Не нашли, что искали? Воспользуйтесь поиском: