
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Многопродуктовая модель управления запасами с ограниченной вместимостью склада
В подавляющем большинстве случаев на предприятии хранится значительный ассортимент n товаров, имеющих определенные размеры и объем.
Предположим, что специалистами из отдела логистики весь ассортимент товара разделен на группы, и каждая группа управляется определенной моделью управления запасами, т.е. рассчитаны оптимальный размер заказа и время поставки. Рассчитаем площадь, которую занимает весь ассортимент товаров. Может оказаться, что она больше площади склада. В данном случае перед отделом логистики ставится задача уменьшения количества товаров, хранимых на складе, за счет корректировки оптимального размера заказа. Математическая модель данной задачи имеет вид:
 , (1.5.1)
, (1.5.1)
где
СЗ – суммарные затраты на хранение и доставку всех товаров, руб.;
Аi – стоимость оформления (подачи) заказа на поставку i-го товара, руб.;
Si – потребность в i-ом товаре в единицу времени, шт;
Qi – оптимальный размер заказа на поставку i-го товара, шт.;
Wi – стоимость хранения единицы i-го товара.
при ограничениях:
 , (1.5.2)
, (1.5.2)
 ,
,
i – целое положительное число.
где
аi – площадь, занимаемая при хранении i-го товара, м2;
N – площадь склада, м2.
Если весь ассортимент товаров на складе можно разделить на группы по степени важности, то сокращение оптимального размера заказа происходит за счет наименее прибыльных. В случае если рассматривается группа товаров, взаимоувязанных между собой или имеющих высокие издержки на хранение и относительно стабильный спрос, то для корректировки оптимального размера заказа можно использовать метод множителей Лагранжа.
Построим функцию Лагранжа:
 , (1.5.3)
, (1.5.3)
 , (1.5.4)
, (1.5.4)
где
l - множитель Лагранжа (l≤0).
Представим (1.5.4) в более удобном для дальнейшего анализа виде:
 ,
,
или
 (1.5.5)
(1.5.5)
где
Li – слагаемое, соответствующее скорректированным суммарным затратам на поставку i-го товара,  .
.
Оптимальные значения Q* и l* находятся из следующей системы уравнений (необходимые условия для экстремума функции Лагранжа):
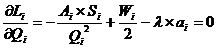 (1.5.6)
(1.5.6)
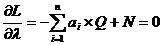 .
.
Из формулы (1.5.6) найдем скорректированный оптимальный размер заказа для каждого товара:
 . (1.5.7)
. (1.5.7)
Алгоритм решения:
1 шаг. Для каждого товара рассматриваемой группы определить оптимальный размер заказа по формуле Уилсона (1.1.5).
2 шаг. Определить суммарную площадь, занимаемую всеми товарами, и коэффициент использования склада:
 . (1.5.8)
. (1.5.8)
Если Ku >1 (рассчитанная площадь больше площади склада или выходит за заданные в задаче ограничения), то следует перейти к шагу три, в противном случае расчет прекращается.
3 шаг. Рассчитывать значение скорректированного оптимального размера заказа для каждого товара по формуле 1.5.7, уменьшая значение множителя Лагранжа, до тех пор, пока не будет соблюдено ограничение 1.5.2. или достигнуто требуемое значение Ku.
Задача
Предприятие планирует выделить 135 м2 для хранения трех видов товаров, обладающих стабильным спросом. Затраты на хранение, потребность, стоимость подачи заказа и занимаемая площадь для всех товаров отражены в таблице. Определить оптимальный размер заказа для трех товаров, чтобы коэффициент использования склада был больше 0,96.
| Товар | А, руб. | S, т./день | W, руб./сутки | а, м2 |
| 1,7 | ||||
| 3,1 | 1,5 |
Решение
Определим оптимальный размер заказа для каждого товара по формуле Уилсона:
 т.;
т.;
 т.;
т.;
 т.
т.
Рассчитаем суммарную площадь, занимающую партией товаров:
 м2;
м2;
 м2;
м2;
 м2;
м2;
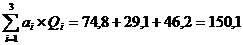 м2.
м2.
Так как суммарная площадь товаров превышает размеры склада, то для определения оптимального размера заказа воспользуемся формулой 1.5.7. Расчет будем вести в табличной форме.
| l | Q1 | Q2 | Q3 | a1 x Q1 | a2 x Q2 | a3 x Q3 | 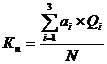
|
| -0,1 | 34,2 | 27,5 | 29,4 | 68,4 | 27,5 | 44,1 | 1,04 |
| -0,2 | 31,6 | 26,2 | 28,2 | 63,2 | 26,2 | 42,3 | 0,97 |
| -0,3 | 29,6 | 27,1 | 59,2 | 40,65 | 0,92 |
При l = -0,2 коэффициент использования склада будет больше 0,96 и равен 97 %. Таким образом, оптимальный размер заказа для первого, второго и третьего товара равен 31,6 т., 26,2 т. и 28,2 т. соответственно.
Задачи
1. Объем продаж телевизоров составляет в месяц 4000 шт. Стоимость хранения одного телевизора в год обходится магазину в 210 у.е. За доставку заказа владелец магазина должен заплатить 100 у.е. Время доставки телевизоров 15 дней, возможное время задержки 3 дня. Определить оптимальную стратегию управления запасами и дать графическое представление стратегии.
2. Спрос на продукцию компании составляет 2100 шт. в месяц. Издержки на хранение единицы продукции составляют 0,7 у.е./день. Стоимость подачи заказа составляет 300 у.е. Время доставки продукции 12 дней, возможное время задержки 2 дня. Определить параметры системы управления запасами с фиксированным размером заказа и дать графическую модель системы
3. Предприятие желает определить оптимальный размер заказа для каждого из трех видов продукции таким образом, чтобы коэффициент использования склада был равен 0,96. Площадь склада 140 м2.
| Товар | Стоимость подачи заказа, у.е. | Потребность, дн. | Затраты на хранение, у.е./день | Площадь товара, м2 |
| 0,3 | 1,1 | |||
| 0,2 | 0,7 | |||
| 0,1 | 2,4 |
4. Для производства трехколесного велосипеда компания заказывает колеса по цене 100 у.е./шт. Годовая потребность в велосипедах составляет 4000 шт. Издержки на хранение одного колеса на складе составляют 0,4 у.е./день. Стоимость подачи заказа составляет 120% от стоимости колеса. Время поставки партии колес – 11 дней, возможное время задержки – 2 дня. Определить параметры системы управления запасами с фиксированным интервалом времени между заказами и дать графическую модель системы.
5. Определить оптимальный размер заказа для трех видов продукции таким образом, чтобы количество заказов в год (365 дней) для каждого вида товара составляло не более 110, 120 и 115 соответственно.
| Товар | Стоимость подачи заказа, у.е. | Потребность, дн. | Затраты на хранение, у.е./день |
| 0,4 | |||
| 0,5 | |||
| 0,4 |
6. Стулья продаются по 30 у.е. за штуку, но предполагается 15% скидка при покупке партии 130 шт. и более. Квартальная потребность в стульях для компании составляет 120 шт., стоимость подачи заказа составляет 70 у.е. Издержки на хранение единицы товара на складе составляет 0,4 у.е./день. Определить оптимальную стратегию управления запасами.
7. Определить оптимальный размер заказа для 4-х видов товаров, если площадь склада равна 140 м2.
| Товар | Стоимость подачи заказа, у.е. | Потребность, дн. | Затраты на хранение, у.е./день | Площадь товара, м2 |
| 0,3 | 1,2 | |||
| 0,3 | 0,9 | |||
| 0,4 | 0,8 | |||
| 0,4 | 1,4 |
8. Ежегодная потребность в материалах для строительства составляет 3200 т. Стоимость подачи заказа – 230 у.е. Затраты на хранения одной тонны материалов на складе составляет 0,9 у.е. в сутки. Время доставки материалов на строительную площадку составляет 17 дней, максимально возможное время задержки в поставке составляет 2 дня. Определить оптимальную стратегию управления запасами и дать графическое представление модели.
9. Для изготовления люстр с тремя лампочками компания заказывает лампочки по цене 10 у.е. за штуку. Годовая потребность в люстрах составляет 4300 штук. Стоимость подачи заказа составляет 250 у.е. Издержки на хранение одной лампочки на складе обходится компании в 5,6% от стоимости лампочки в день. Время доставки материалов на строительную площадку составляет 14 дней, максимально возможное время задержки в поставке составляет 1 день. Определить параметры системы управления запасами с фиксированным интервалом времени между заказами и дать графическую модель системы.
10. Стоимость одного блокнота для компании составляет 15 у.е. Цена может быть снижена до 10 у.е. при покупке от 230 блокнотов и более. Дневная потребность в блокнотах – 10 шт. Стоимость подачи заказа составляет 120 у.е. Затраты на хранение одного блокнота на складе обходятся в 0,05 у.е. Время доставки товара составляет 11 дней, максимальное время задержки – 2 дня. Определить оптимальную стратегию управления запасами.
11. Определить оптимальный размер заказа для 4-х видов товаров, если площадь склада равна 120 м2.
| Товар | Стоимость подачи заказа, у.е. | Потребность, дн. | Затраты на хранение, у.е./день | Площадь товара, м2 |
| 0,3 | 1,2 | |||
| 0,2 | 1,9 | |||
| 0,4 | 0,8 | |||
| 0,4 | 1,4 |
12. Спрос на продукцию компании составляет 1700 шт. в месяц. Издержки на хранение единицы продукции составляют 0,56 у.е./день. Стоимость подачи заказа составляет 700 у.е. Время доставки продукции – 10 дней, возможное время задержки – 2 дня. Определить параметры системы управления запасами с фиксированным размером заказа и дать графическую модель системы.
13. Объем продаж стиральных машин составляет в месяц 500 шт. Хранение одной стиральной машины в год обходится магазину в 260 у.е. За доставку заказа владелец магазина должен заплатить 120 у.е. Время доставки стиральных машин 18 дней, возможное время задержки 2 дня. Определить оптимальную стратегию управления запасами и дать графическое представление стратегии.
14. Стоимость одного стула для компании составляет 18 у.е. Цена может быть снижена до 13 у.е. при покупке от 170 стульев и более. Дневная потребность в стульях – 10 шт. Стоимость подачи заказа составляет 98 у.е. Затраты на хранение единицы товара на складе – в 0,05 у.е. в день. Время доставки товара составляет 9 дней, максимальное время задержки – 1 день. Определить оптимальную стратегию управления запасами.
15. Для изготовления люстр с двумя лампочками компания заказывает лампочки по цене 8 у.е. за штуку. Годовая потребность в люстрах составляет 3700 штук. Стоимость подачи заказа составляет 220 у.е. Издержки на хранение одной лампочки на складе для компании в день составляют 5,6% от стоимости лампочки. Время доставки заказа составляет 12 дней, максимально возможное время задержки в поставке составляет 2 дня. Определить параметры системы управления запасами с фиксированным интервалом времени между заказами и дать графическую модель системы.
16. Объем продаж телефонов составляет в месяц 1500 шт. Стоимость хранения одного телефона в год обходится магазину в 120 у.е. За доставку заказа владелец магазина должен заплатить 80 у.е. Время доставки телефонов – 14 дней, возможное время задержки – 1 день. Определить оптимальную стратегию управления запасами и дать графическое представление стратегии.
17. Спрос на продукцию компании составляет 1600 шт. в месяц. Издержки на хранение единицы продукции составляют 0,72 у.е./день. Стоимость подачи заказа составляет 110 у.е. Время доставки продукции – 20 дней, возможное время задержки – 2 дня. Определить параметры системы управления запасами с фиксированным размером заказа и дать графическую модель системы.
18. Стоимость одного календаря обходится компании в 11 у.е. Цена может быть снижена до 9 у.е. при покупке от 145 календарей и более. Дневная потребность в календарях – 15 шт. Стоимость подачи заказа составляет 75 у.е. Затраты на хранение одного товара на складе обходится в 0,5 у.е. Время доставки товара составляет 12 дней, максимальное время задержки – 2 дня. Определить оптимальную стратегию управления запасами.
19. Для изготовления наручных часов компания заказывает кожаные и металлические ремни (для одних часов) по цене 9 у.е. за штуку. Годовая потребность в часах составляет 4700 штук. Стоимость подачи заказа составляет 195 у.е. Издержки на хранение одних часов на складе обходится компании в 6% от стоимости часов в день. Время доставки составляет 5 дней, максимально возможное время задержки в поставке составляет 2 дня. Определить параметры системы управления запасами с фиксированным интервалом времени между заказами и дать графическую модель системы.
20. Спрос на продукцию компании составляет 2540 шт. в месяц. Издержки на хранение единицы продукции составляют 0,35 у.е./день. Стоимость подачи заказа составляет 150 у.е. Время доставки продукции – 4 дня, возможное время задержки – 2 дня. Определить параметры системы управления запасами с фиксированным размером заказа и дать графическую модель системы
Не нашли, что искали? Воспользуйтесь поиском: