
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 15. Электромагнитные волны в средах. Дисперсия, 6ч.
15.1. В низкочастотном приближении комплексная диэлектрическая проницаемость проводника может быть представлена в виде:  . Найти коэффициенты преломления
. Найти коэффициенты преломления  и поглощения
и поглощения  (
( ) как функции проводимости и частоты и изучить их поведение при
) как функции проводимости и частоты и изучить их поведение при  и при
и при  .
.
15.2. Получить выражение для диэлектрической проницаемости  в высокочастотном пределе, когда заряженные частицы можно рассматривать как свободные.
в высокочастотном пределе, когда заряженные частицы можно рассматривать как свободные.
15.3. Эффективная проводимость среды, содержащей  электронов в одном кубическом сантиметре, определяется выражением
электронов в одном кубическом сантиметре, определяется выражением  на частоте
на частоте  , где
, где  и
и  - заряд и масса электрона соответственно. Пользуясь уравнениями Максвелла, получить выражение для скорости распространения электромагнитных волн в такой среде.
- заряд и масса электрона соответственно. Пользуясь уравнениями Максвелла, получить выражение для скорости распространения электромагнитных волн в такой среде.
15.4.* Диэлектрическая проницаемость среды, состоящей из атомов, рассматриваемых в осцилляторном приближении, имеет вид:  , где
, где  - число электронов в единице объема,
- число электронов в единице объема,  ,
,  - заряд и масса электрона;
- заряд и масса электрона;  ,
,  и
и  - постоянные. Показать, что данная формула удовлетворяет дисперсионным соотношениям Крамерса-Кронига.
- постоянные. Показать, что данная формула удовлетворяет дисперсионным соотношениям Крамерса-Кронига.
15.5.* Найти зависимость частоты  электромагнитного поля от волнового вектора
электромагнитного поля от волнового вектора  в плазменной среде при условии, что частота электромагнитного поля больше плазменной частоты
в плазменной среде при условии, что частота электромагнитного поля больше плазменной частоты  .
.
Волновые пакеты
15.6. Построить одномерный волновой пакет  ,
,  , взяв в качестве амплитудной функции кривую вида:
, взяв в качестве амплитудной функции кривую вида:  , где
, где  ,
, 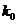 и
и  - постоянные. Найти связь между шириной пакета
- постоянные. Найти связь между шириной пакета  и интервалом волновых чисел
и интервалом волновых чисел  , вносящих основной вклад в суперпозицию.
, вносящих основной вклад в суперпозицию.
15.7.* Волновой пакет образован суперпозицией плоских волн с разными частотами  . Амплитудная функция имеет вид
. Амплитудная функция имеет вид 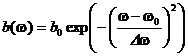 , где
, где  ,
,  и
и  - постоянные. Найти зависимость амплитуды пакета
- постоянные. Найти зависимость амплитуды пакета  от времени.
от времени.
15.8.* Найти фазовую  и групповую
и групповую  скорости распространения волн в среде, диэлектрическая проницаемость которой описывается выражением
скорости распространения волн в среде, диэлектрическая проницаемость которой описывается выражением  , где
, где  и
и  -некоторые константы.
-некоторые константы.
15.9.* Показать, что произведение фазовой  и групповой
и групповой  скоростей волны, распространяющейся в плазме с диэлектрической проницаемостью
скоростей волны, распространяющейся в плазме с диэлектрической проницаемостью  , равно
, равно  .
.
Не нашли, что искали? Воспользуйтесь поиском: