
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Составляющие энергетического баланса
Радиационный баланс земной поверхности равен разности поглощенной солнечной радиации и длинноволнового эффективного излучения:
R = Q *(1 – α) –I, где (1)
| R | - радиационный баланс земной поверхности; |
| Q | - суммарная коротковолновая радиация (сумма прямой и рассеянной радиации); |
| α | - альбедо (отражательная способность земной поверхности для суммарной радиации), выраженное в долях единицы; |
| I | - эффективное излучение, т.е. разность собственного излучения земной поверхности и поглощаемого на поверхности противоизлучения от атмосферы. |
Аналогичным образом можно определить радиационный баланс системы Земля-атмосфера, т.е. радиационный баланс вертикального столба, проходящего через всю толщу атмосферы до земной поверхности. В этом случае получим
Rs = Qs *(I – αs) – Is, где (2)
| Qs | - солнечная радиация, приходящаяся на внешнюю границу атмосферы; |
| αs | - альбедо системы; |
| Is | - длинноволновое излучение с внешней границы атмосферы в мировое пространство (уходящее излучение). |
Радиационный баланс атмосферы Ra равняется разности величин Rs и R. Используя формулы (1) и (2), получим
Ra = Qs *(I – αs) – Q *(I – α) – (Is - I)
Условия отражения солнечной радиации от земной поверхности характеризуется значением альбедо, равным отношению отраженной радиации к приходящей радиации. Теоретически значения альбедо могут изменяться от единицы для абсолютно белой, полностью отражающей поверхности до нуля для абсолютно черной поверхности, полностью поглощающей солнечные лучи.
Условия поглощения солнечной радиации на водоемах отличаются от условий поглощения на поверхности суши. Более или менее чистая вода сравнительно хорошо прозрачна для коротковолновой радиации, вследствие чего солнечные лучи, проникающие в верхние слой водоема, многократно рассеиваются и после этого в значительной мере поглощаются. Если солнце стоит более или менее высоко, значительная часть приходящей радиации проникает в верхние слои водоема и там в основном поглощается. При низких высотах солнца лучи, падающие на водную поверхность под малыми углами, зеркально отражаются и не проходят в глубины водоема. Это приводит к резкому увеличению альбедо.
Альбедо системы Земля-атмосфера имеет более сложную природу по сравнению с альбедо земной поверхности. Приходящая в атмосферу солнечная радиация частично отражается в результате обратного рассеивания атмосферы. При наличии облаков значительная часть радиации может отражаться от их верхней поверхности. При полном или частичном отсутствии облаков альбедо системы Земля-атмосфера существенно зависит от альбедо земной поверхности. Альбедо облаков зависит от толщины их слоев. Альбедо системы Земля-атмосфера при отсутствии облаков обычно больше альбедо земной поверхности, при наличии облаков альбедо системы также обычно больше альбедо земной поверхности, кроме случаев, когда поверхность покрыта более или менее чистым снегом. Наряду с отражением коротковолновой радиации не менее существенной формой расходования радиационной энергии является длинноволновое излучение. Значительная часть потока длинноволновой радиации, излучаемой земной поверхностью, компенсируется противоизлучением атмосферы. Длинноволновое излучение атмосферы при отсутствии облаков в основном определяется наличием водяного пара и углекислого газа. Как водяной пар, так и углекислый газ поглощают длинноволновое излучение главным образом в определенных спектральных областях. Наиболее сильное поглощение водяным паром происходит в области длин волн 5-7.5 мкм, тогда как в области 9-12 мкм поглощение излучения сравнительно не велико. Углекислый газ имеет несколько полос поглощения, из которых наибольшее значение имеет полоса с длинами волн 13-17 мкм. Следует отметить, что содержание углекислого газа в атмосфере изменяется сравнительно мало, тогда как количество водяного пара может быть очень различным в зависимости от метеорологических условий. Поэтому изменение влажности воздуха оказывается существенным фактором, влияющим на величину излучения атмосферы. Противоизлучение атмосферы обычно значительно возрастает при наличии облаков. В таких условиях эффективное излучение определяется в основном разностью температур земной поверхности и нижней поверхности облаков. Если эта разность невелика, то эффективное излучение также приближается к нулю. Таким образом, эффективное излучение земной поверхности зависит главным образом от температуры земной поверхности, влагосодержания воздуха и облачности. В зависимости от этих факторов эффективное излучение может изменяться от значений близких к нулю, до нескольких сот Вт/м2.
Уравнения энергетического (теплового) баланса представляют собой частные формулировки одного из основных физических законов – закона сохранения энергии. Эти уравнения могут быть составлены для различных объемов и поверхностей в атмосфере, гидросфере и литосфере. Наиболее часто используются уравнение баланса для участка поверхности Земли и уравнение баланса для системы Земля-атмосфера, т.е для вертикальной колонны, проходящей через всю внешнюю оболочку Земли. Уравнение энергетического баланса земной поверхности включает потоки энергии между элементом поверхности и окружающим пространством. В число этих потоков входят радиационные потоки тепла, сумма которых равна радиационному балансу. Так как температура земной поверхности обычно не равна температуре воздуха, то между подстилающей поверхностью и атмосферой возникает поток тепла, обусловленный молекулярной и, главным образом, турбулентной теплопроводностью. Существенное значение в энергетическом балансе земной поверхности обычно имеет расход тепла на испарение. Испарение зависит от увлажнения земной поверхности, ее температуры, влажности воздуха и интенсивности турбулентного обмена в приземном слое воздуха, которая определяет скорость переноса водяного пара от поверхности Земли в атмосферу.Для составления уравнения энергетического баланса будем обозначать радиационный поток тепла через R, турбулентный поток тепла от земной поверхности к атмосфере через P, поток тепла от земной поверхности к нижележащим слоям через А и затрату тепла на испарение (или выделение тепла при конденсации) через LE (L – удельная теплота парообразования, Е – скорость испарения). Так как все другие члены баланса обычно значительно меньше перечисленных здесь потоков тепла, то в первом приближении уравнение энергетического баланса можно записать в форме R = LE + P + A.
При этом значение баланса считается положительным, если оно характеризует приход энергии к земной поверхности, а все остальные значения считаются положительными, когда они характеризуют расход энергии. Схема потоков тепла, включенных в уравнение энергетического баланса, представлены на рис. 1.
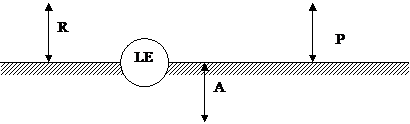
Рис. 1 Схема энергетического баланса земной поверхности.
Из членов энергетического баланса, не включенных в это уравнение, наиболее значительным по величине может быть расход тепла на таяние льда или снега на земной поверхности (или приход тепла от замерзания воды). Хотя для большинства периодов осреднения (например, для года) эта величина, как правило, оказывается значительно меньшей по сравнению с основными членами баланса, для некоторых случаев (например, для времени снеготаяния в областях средних и высоких широт) ее следует включать в это уравнение в качестве дополнительного члена.
Поток А от земной поверхности к нижележащим слоям можно определить по другим составляющим энергетического баланса верхних слоев литосферы или гидросферы. Если мы составим уравнение энергетического баланса для вертикальной колонны, верхнее основание которой расположено на земной поверхности. А нижнее лежит на достаточно большой глубине, то получим уравнение
A = B + Fo
где Fo – приход тепла, обусловленный теплообменом колонны с окружающим пространством лито- или гидросферы по горизонтали; В – изменение теплосодержания внутри колонны за данный интервал времени (рис. 2).
 |
Рис. 2Схема энергетического баланса верхнего слоя литосферы или гидросферы
Член Fo приобретает большое значение в обширных водоемах, где существуют течения и имеет место большая горизонтальная теплопроводность, обусловленная действием макротурбулентности.
Для условий литосферы величина Fo, как правило, незначительна вследствие малости теплопроводности почвы. Поэтому для суши А = В. Так как в среднем за год верхние слои почвы не охлаждаются и не нагреваются, то для среднего многолетнего годового периода в условиях суши А = В = 0
Таким образом, для среднего годового периода уравнение энергетического баланса суши имеет вид
R = LE + P,
а уравнение энергетического баланса для условий замкнутого водоема (океана)
R = LE + P + Fo
для условий пустыни, где испарение близко к нулю, уравнение приобретает форму R = P. Для условий Мирового океана в целом, когда общее перераспределение тепла течениями вследствие взаимной компенсации равно нулю, уравнение приобретает вид
R = LE + P
Для вывода уравнения энергетического баланса системы Земля- атмосфера следует рассмотреть приход и расход тепловой энергии в вертикальной колонне, проходящей через всю атмосферу и верхние слои гидро- и литосферы, вплоть до уровней, где прекращаются заметные сезонные (или суточные) колебания температуры. Теплообмен между выделенной колонной и мировым пространством характеризуется ее радиационным балансом Rs равным разности поглощенной солнечной радиации во всем объеме колонны и общего длинноволнового излучения из этого объема (рис. 3). Величина Rs считается положительной, когда она характеризует приход тепла к системе Земля-атмосфера.
Кроме теплообмена через поверхность колонны, на ее энергетический баланс существенно влияют источники и стоки тепла, расположенные внутри самой колонны. Среди них основное значение имеют приход и расход тепла, возникающий вследствие процессов фазовых превращений воды, в особенности в результате испарения и конденсации.
Приход тепла от конденсации в атмосфере равен разности прихода и расхода тепла, связанных с конденсацией и испарением капель воды в облаках и туманах. Над достаточно однородной поверхностью для значительных периодов осреднения разность значений конденсации и испарения в атмосфере равна сумме осадков r, в этом случае приход тепла равен Lr. Соответствующий член энергетического баланса представляет собой разность прихода тепла от конденсации и расход при испарении капель. Он может, однако, отличаться от величины Lr в условиях пересеченной местности, а также для отдельных коротких интервалов времени.
Расход тепла на испарение с земной поверхности (разность расхода тепла на испарение с поверхности водоемов, почв и растительности и прихода тепла от конденсации на этих поверхностях) равен Lr. Общее влияние конденсации и испарения на энергетических Балан колонны можно приближенно охарактеризовать величиной L(r-E).
Из других членов энергетического баланса колонны следует учесть изменение теплосодержания внутри колонны за интервал времени суммирования Bs. Остальные члены баланса (приход тепла от диссипации механической энергии, разность расход тепла на таяние льда и прихода от его образования, разность расхода тепла на фотосинтез и прихода от окисления органического вещества и т.д.) обычно не играют заметной роли в энергетическом балансе системы Земля-атмосфера и могут не учитываться.

Рис. 3Схема энергетического баланса системы Земля-атмосфера.
Записывая уравнение энергетического баланса системы Земля-атмосфера в форме
Rs = Fs + L(E - r) + Bs
где Fs = Fa + Fo будем считать все члены правой части положительными, если они характеризуют расход тепла. Для среднего годичного периода величина Bs близка к нулю и уравнение принимает вид
Rs = Fs + L(E - r)
Для условий суши это уравнение имеет вид
Rs = Fa + L(E - r)
Так как для всего земного шара за год E = r и горизонтальный приток тепла в атмосфере и гидросфере равна нулю, то уравнение энергетического баланса для всей системы Земля-атмосфера приобретает форму
Rs = 0
Уравнение энергетического баланса атмосферы можно получить либо как сумму соответствующих потоков тепла, либо просто как следствие энергетического баланса системы Земля-атмосфера и земной поверхности.
Учитывая, что радиационный баланс атмосферы
Ra = Rs – R,
а изменение теплосодержания в атмосфере
Ва = Bs – B,
найдем, что
Ra = Fs + L(E – r) + Bs – Fo – P – LE - B
Ra = (Fs + Fo) + LE – Lr + (Bs - B) – P - LE
Ra = Fa – Lr - P + Bs
причем для среднего годичного периода
Ra = Fa – Lr - P
Не нашли, что искали? Воспользуйтесь поиском: