Самовозбуждение простейшего автогенератора

Исследова­ние процессов в автогенераторах начнем с устройства рисунок (5.1), называемого автогенератором с трансформатор­ной связью.

Колебательной системой здесь служит LCR-контур, элементом обратной связи — катушка L_СВ, размешенная таким образом, что создаваемый ею магнитный поток частично пронизывает катушку L.

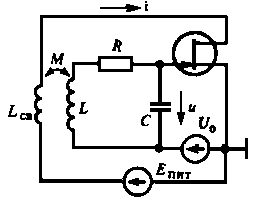
Рисунок 1 – Схема автогенератора с трансформаторной связью

Пусть в устройстве каким-либо образом возбуждены малые колебания. Если u - напряжение на конденсаторе (и соответственно на управляющем электроде электронного прибора), то по второму закону Кирхгофа можно составить следующее дифференциальное уравнение, описывающее данную систему:

, (1)

где i - ток в цепи обратной связи. Знак в правой части (1) зависит от того, каким образом (встречно или согласно) включены катушки L и L_СВ.

Сделаем основное предположение — будем считать управляющее напряжение uстоль малым, что электронный прибор вполне точно может быть заменен управляемым источником тока, выходной сигнал которого линейно зависит от управляющего напряжения:

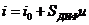(2)

Здесь i₀ - постоянная составляющая тока; S_ДИФ - дифференциальная крутизна вольт-амперной характеристики в фиксированной рабочей точке.

Объединив выражения (1) и (2), получаем следующее уравнение системы:

, (3)

где 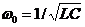- частота собственных колебаний контура без потерь.

Варьируя коэффициент взаимоиндукции М, можно изменять коэффициент при производной du/dt. Знак и значение этого коэффициента, как известно, определяют характер свободных колебаний в такой динамической системе.

Если в уравнениях (1) и (3) выбраны верхние зна­ки, то за счет обратной связи будет наблюдаться регенерация. Если величина Мдостигает критического значения

, (4)

где Q –добротность контура без учета регенерации, то уравнение (3) приобретает вид , свойственный идеальной колебательной системе без потерь.

При М > М_КР устройство становится неустойчивым. Введя параметр

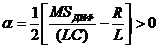, (5)

получим дифференциальное уравнение

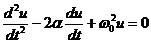, (6)

решение, которого описывает гармонические колебания с экспоненциально нарастающей во времени амплитудой:

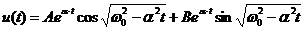(7)

(А и В — постоянные, зависящие от начальных условий).

Практически всегда 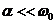и в соответствии с (7) частота заполнения автоколебаний, возникающих в линейном режиме, близка к частоте собственных колебаний контура.

Подчеркнем физический смысл правильного выбора знака в уравнении (3), который обеспечивает неустойчивость начального состояния автогенератора: для самовозбуждения системы необходимо, чтобы любое возмущение колебательного контура приводило к появлению такого сигнала положительной обратной связи, который, складываясь с первоначальным возмущением, увеличивал бы его. Именно таким образом трактуется понятие положительной обратной связи в теории автоколебательных систем.

Не нашли, что искали? Воспользуйтесь поиском: