
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод укороченного уравнения
Обратимся к простейшей схеме автогенератора с трансформаторной связью и будем считать заданной вольт-амперную характеристику активного элемента i=f(u). Посколькуdi/dt=df/du*du/dt, запишем нелинейное дифференциальное уравнение (1), характеризующее поведение автогенератора при любых режимах, в виде:
 (16)
(16)
Способов точного решения таких уравнений при любой функции f(u) не существует. Приходится использовать те или иные дополнительные соображения физического характера и отыскивать приближенные решения. В данном случае следует принять во внимание, что автогенератор содержит высокодобротный колебательный контур. Поэтому, несмотря на присутствие нелинейного элемента, напряжение на контуре должно мало отличаться от гармонического колебания с частотой 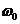 .
.
Будем искать приближенное решение уравнения (16) ввиде:
 (17)
(17)
предполагая амплитуду U(t) медленной функцией в том смысле, что 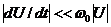 . На этом основании в выражении первой производной
. На этом основании в выражении первой производной
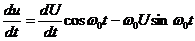 (18)
(18)
сохраним только второе слагаемое:
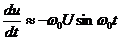 (19)
(19)
Таким же образом вторая производная
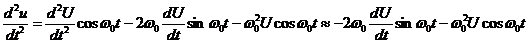 (20)
(20)
Подставив выражения (19) и (20) в (16) получим так называемое укороченное дифференциальное уравнение
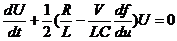 (21)
(21)
Переход к укороченному уравнению значительно упрощает последующие этапы анализа, так как при этом порядок дифференциального уравнения снижается на единицу.
Не нашли, что искали? Воспользуйтесь поиском: