
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Рекомендации к выполнению 2 задачи.
Сигнал управления приводом и формируется с помощью обратной связи по отклонению температуры х в помещении от задания у:
ε(t)=y(t)-x(t)
где t — текущее время.
Управляющий элемент (регулятор) системы реализует пропорционально-интегралъный алгоритм, то есть вырабатывает управляющее воздействие u(t) пропорциональное сумме отклонения и интеграла по времени от этого отклонения:
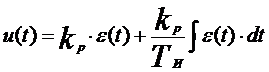 ,
,
где kР и ТИ — коэффициент передачи и постоянная времени интегрирования (параметры настройки) регулятора (задача 3).
Для обозначения функций времени используем строчные буквы, а для обозначения их изображений— соответствующие прописные, например:


где u(t), r(t) —функции времени; U(s) —. изображение Лапласа функции u(t); R(iw) — изображение Фурье функции r(t); 

 s=s + iw -комплексная переменная.
s=s + iw -комплексная переменная.
Передаточная функция исполнительных механизмов, т.е. электроприводов можно выбрать из табл. 4.
Таблица 4. Выбор передаточных функций ЭП.
| Апериодическое второго порядка | 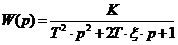 T-постоянная времени
K-коэффициент передачи
T-постоянная времени
K-коэффициент передачи
 -коэффициент демпфирования( -коэффициент демпфирования(  1) 1)
| 
| Электродвигатель постоянного тока независимого возбуждения
Входная-UЯ Выходная-wд
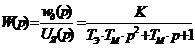
  ,-электромагнитпая и электромеханическая постоянные K=5…10 ,-электромагнитпая и электромеханическая постоянные K=5…10  =0.015..0.02сек =0.015..0.02сек  =0.002…0.005сек =0.002…0.005сек
|
| Интегрирующее |  K-коэффициент передачи
K-коэффициент передачи
| 
| Электродвигательный исполнительный механизм
Вход-U Выход-угол поворота вала редуктора  K=2…8рад/с*В K=2…8рад/с*В
|
| Запаздываю-щее | 
 -время запаздывания -время запаздывания
| 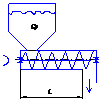
| Шнековый транспортёр
Вход-расход на входеQ1
Выход-расход на выходеQ2
 , , 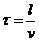
 =tзап=2…8 сек. =tзап=2…8 сек.
|
При выполнении данного раздела параметры К, Т и t необходимо рассчитывать по приведенным в табл. 6.1 формулам в зависимости от типа ЭП, а на практике их часто определяются экспериментально по временной характеристике объекта. Для этого с помощью самопишущего прибора записывается изменение во времени температуры х(t), вызванное скачкообразным изменением управляющего сигнала u(t) (рис. 16).
Рисунок 16
 |
Реакция объекта x(t) на скачкообразное воздействие u(t)
Далее для решения этой задачи необходимо определить устойчивость системы управления. Для этого допустим kr=1,9; Θ=100c; τ=50c.
Находим передаточную функцию системы в разомкнутом состоянии, когда сигнал х не поступает на вход сумматора и ε= у (рис. 15):
 , где К – безразмерный коэффициент передачи разомкнутой системы из табл. 4.
, где К – безразмерный коэффициент передачи разомкнутой системы из табл. 4.
Подставляя полученное выражение для W(s) в общее выражение для передаточной функции замкнутой системы:
 , (30)
, (30)
находим передаточную функцию рассматриваемой замкнутой системы:
 , (31)
, (31)
где знаменатель есть левая часть характеристического управления системы в замкнутом состоянии, то есть
(Тs2 + s)eτs + Кs + k/Tи = 0.
Не нашли, что искали? Воспользуйтесь поиском: