Определяем устойчивость системы.

По критерию Найквиста.

Подставляя s = iω в выражение для W_(s), построим в комплексной плоскости график комплексной частотной характеристики разомкнутой системы W(iω) при К = 1, Т_и = 25 с.

Для этого сначала построим КЧХ апериодического звена.

График этой КЧХ представляет собой полуокружность, расположенную в четвертом квадранте комплексной плоскости. Радиус полуокружности равен К/2, а ее центр расположен на положительной вещественной полуоси на расстоянии К/2 от начала координат.

Рисунок 18 Комплексная частотная характеристика
апериодического звена

Задаваясь значениями ω, вычислим несколько (4…5) значений угла 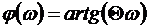и строим (4…5) векторов КЧХ, используя транспортир. Значения ω рекомендуется выбирать в таком промежутке ω_*≤ω≤ω_**, чтобы соответствующие значения угла φ равномерно располагались в секторе 45º≤φ≤80º. Значения ω_* и ω_** легко вычислить по формулам:

;

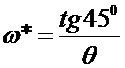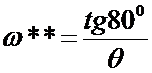
Модули построенных векторов А можно вычислить по формуле

однако вместо вычислений проще измерить их с помощью обычной линейки.

Затем построим годограф КЧХ объекта W₀ (iω). Для этого, использую циркуль и транспортир, повернем каждый вектор W_r(iω) на угол β = ωτ по часовой стрелке, то есть угол векторов КХЧ объекта ά = φ + β. Использование транспортира предполагает перевод угла β из радианов в градусы:

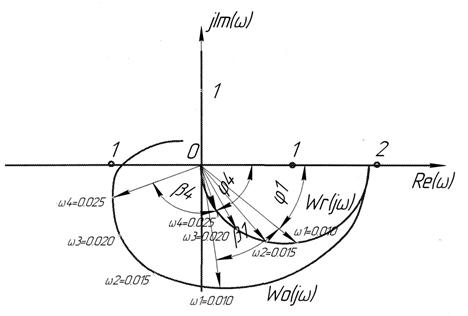
Рисунок 19 Построение комплексной частотной характеристики
объекта

Для построения требуемого участка КХЧ разомкнутой системы W (iω) достаточно располагать участком W₀ (iω) в пределах третьего квадранта комплексной плоскости. Из концов векторов КЧХ объекта на этом участке восстановим к ним перпендикуляры по направлению к отрицательной вещественной полуоси. Длину перпендикуляра определяем по формуле:

Соединяя концы перпендикуляров плавной кривой, получаем годограф КХЧ разомкнутой системы W (iφ) (рис. 20 6.6) при k_r = 1 и
Т_и = 25 с.

Вывод. Поскольку годограф W (iφ) охватывает точку с координатами (-1, i0), то рассматриваемая система неустойчива. При получении такого вывода необходимо предложить меры по устранению неустойчивости системы.

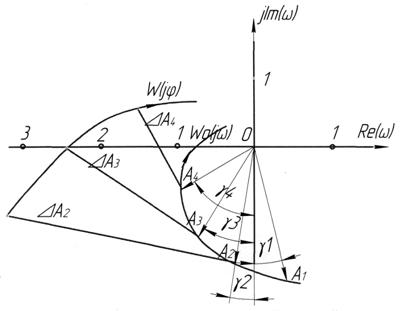
Рисунок 20 Построение требуемого участка комплексной частотной
характеристики разомкнутой системы по соответствующему участку характеристики объекта (γ1=-15,4°; γ2=9,2°;γ3=30,8°;γ4=50,4°)

Не нашли, что искали? Воспользуйтесь поиском: