Прямые методы решения систем линейных уравнений.

Метод Гаусса.

Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Постановка задачи.

Пусть дана система из n линейных уравнений с n неизвестными

х_1, х₂,,х₃…, х_n

(1)

Числа a_ik- называются коэффициентами системы (1), а числа , ,…, - свободными членами. Система (1) называется однородной, если = =…= =0

Матрица А=

называется матрицей системы (или матрицей коэффициентов) (1), а ее определитель |А| - определителем системы (1).

Столбец В =

называется столбцом свободных членов. Если присоединить к матрице А столбец свободных членов, то получим матрицу 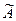, которая называется расширенной матрицей системы:

=

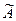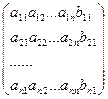
Решением системы (1) называется совокупность чисел , ,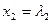..., , 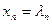которые обращают все уравнения системы в тождества. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной. Совместная система линейных уравнений может иметь одно или несколько решений и называется определенной, если решение единственное и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.

Элементарными преобразованиями системы линейных уравнений называются следующие три типа преобразований:

1) перестановка двух уравнений системы;

2) умножение обеих частей уравнения системы на любое отличное от нуля число;

3) прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Можно доказать, что элементарные преобразования переводят данную систему линейных уравнений в эквивалентную. Выполнение элементарных преобразований равносильно выражению одного неизвестного через другие.

Метод Гаусса применяется для решения систем линейных уравнений, определитель матрицы А которых отличен от 0, такие системы совместны и имеют единственное решение.

Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы, для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Этот этап преобразований называется прямым ходом. На втором этапе, называемом обратным ходом, производятся вычисления значений неизвестных.

Схема единственного деления. Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.

Прямой ход состоит из п - 1 шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного х\ из уравнений с номерами i = 2, 3,..., п. Предположим, что коэффициент 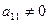. Будем называть его главным (или ведущим) элементом 1-го шага.

Найдем величины (i = 2, 3,..., n),

называемые множителями 1-го шага. Вычтем последовательно из второго, третьего,..., n -го уравнений системы первое уравнение, умноженное соответственно на . Это позволит обратить в нуль коэффициенты при во всех уравнениях, кроме первого. В результате получим эквивалентную систему:

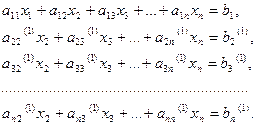
в которой 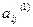и вычисляются по формулам:

, .

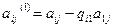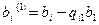2-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами i = 3, 4,..., n. Пусть а₂₂⁽¹⁾ 0, где a ₂₂⁽¹⁾ - коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

(i=3, 4, …, n) и вычтем последовательно из третьего, четвертого,..., n-го уравнения системы второе уравнение, умноженное соответственно на В результате получим систему

Здесь коэффициенты 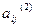и вычисляются по формулам

= -

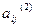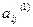Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.

k:-й шаг. В предположении, что главный (ведущий) элемент k-ro шага 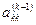отличен от нуля, вычислим множители k-го шага

и вычтем последовательно из (k + 1)-го,..., n-го уравнений полученной на предыдущем шаге системы k-е уравнение, умноженное соответственно на

После (n-1)-го шага исключения получим систему уравнений:

матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы находим . Подставляя найденное значение в предпоследнее уравнение, получим . Осуществляя обратную подстановку, далее последовательно находим 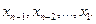. Вычисления неизвестных здесь проводятся по формулам

Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы . Поэтому если один из главных элементов оказывается равным нулю, то схема единственного деления не может быть реализована. Однако, в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности. Поэтому при получении решения системы линейных уравнений обычно производят оценку погрешности и затем уточнение решения.

Это производят следующим образом:

1) вычисляют для каждого уравнения системы невязки — разности между правой и левой частями системы, получающиеся после подстановки в уравнения приближенных значений неизвестных по формулам:

где приближенные значения неизвестных невязки - и свободные члены -

2) выписывают невязки в отдельный столбец;

3) считая столбец е столбцом свободных членов, снова решают по схеме Гаусса исходное уравнение, и получают поправки неизвестных;

4) находят уточненные значения неизвестных, прибавляя к приближенным значениям неизвестных соответствующие поправки

Пример. Дана система линейных уравнений третьего порядка. Решить систему методом Гаусса по схеме единственного деления.

Программа, реализующая метод Гаусса должна содержать следующие последовательно расположенные блоки:

1) ввод исходных данных (матрицы А и столбца свободных членов В);

2) прямой ход, состоящий в делении на главные (ведущие) коэффициенты и последовательном исключении неизвестных с целью приведения матрицы А к верхнему треугольному виду;

3) обратный ход, состоящий в вычислении неизвестных, начиная с последнего;

4) вывод полученного решения.

Program gauss;

{Решение системы лин. уравнений третьего порядка методом Гаусса}

var a:array [1..3.1..3] of real;

b:array [1..3] of real;

x:array [1..3] of real;

ij,k:integer;

d:real;

const n=3;

Begin

writeln ('Введите матрицу А:');

for i:=l to n do

Begin

{....................Ввод исходных данных....................}

for j:=l to n do

Begin

write ('a[',i,’,’,j,']=');

readln(a[i,j]);

End;

End;

writeln ('Введите столбец свободных членов: ');

for i:=l to n do

Begin

write('b[',i,']=');

readln (b[i]);

End;

{................Прямой ход.............}

for i:=l to n-1 do

Begin

for k:=i+l to n do

Begin

d:=a[k,i]/a[i,i];

for j:=i+l to n do

a[k,j]:=a[k,j]-a[I,j]*d;

b[k]:=b[k]-b[i]*d;

End;

End;

{................Обратный ход...........}

for i:=n downto 1 do

Begin

for j:=i+l to n do

b[i]:=b[i]-a[i,j]*x[j];

x[i]:=b[i]/a[i,i];

End;

{..........................Вывод решения................}

writeln('Решение системы линейных уравнений:');

for i:=l to n do

writeln('X[',i,']=',x[i]:l:4);

readln;

End.

Не нашли, что искали? Воспользуйтесь поиском: