Пассивные элементы электрических цепей

Резистивным сопротивлением называется идеализированный элемент электрической цепи, обладающий свойством необратимого рассеивания энергии. Графическое изображение этого элемента и его вольт-амперная характеристика показана на рисунке (а - нелинейное сопротивление, б -линейное сопротивление).

Напряжение и ток на резистивном сопротивлении связаны между собой зависимостями: u = iR, i = Gu. Коэффициенты пропорциональности R и G в этих формулах называются соответственно сопротивлением и проводимостью и измеряются в омах [Ом] и сименсах [См]. R = 1/G.

Индуктивным элементом называется идеализированный элемент электрической цепи, обладающий свойством накопления им энергии магнитного поля. Графическое изображение этого элемента показано на рисунке (а - нелинейного, б - линейного).

Линейная индуктивность характеризуется линейной зависимостью между потокосцеплением ψ и током i, называемой вебер-амперной характеристикой ψ= Li. Напряжение и ток связаны соотношением u = dψ/dt = L(di/dt)

Коэффициент пропорциональности L в формуле и называется индуктивностью и измеряется в генри (Гн).

Емкостным элементом (емкостью) называется идеализированный элемент электрической цепи, обладающий свойством накапливания энергии электрического поля. Графическое изображение этого элемента показано на рисунке. (а - нелинейного, б - линейного).

Линейная емкость характеризуется линейной зависимостью между зарядом и напряжением, называемой кулон-вольтовой характеристикой q = Cu

Напряжение и ток емкости связаны соотношениями i = dq/dt =C(du/dt)

Билет 11

Акт Активные элементы электрических цепей

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

Источник напряжения - идеализированный элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока.

Внутреннее сопротивление идеального источника напряжения равно нулю.

Источник тока – это идеализированный элемент электрической цепи, ток которого не зависит от напряжения на его зажимах.

Внутреннее сопротивление идеального источника тока равно бесконечности.

Источники напряжения (тока) называются зависимыми (управляемыми), если величина напряжения (тока) источника зависит от напряжения или тока другого участка цепи. Зависимыми источниками моделируются электронные лампы, транзисторы, усилители, работающие в линейном режиме.

Различают четыре типа зависимых источников.

1. ИНУН – источник напряжения, управляемый напряжением: а) нелинейный, б) линейный, μ – коэффициент усиления напряжения

2. ИНУТ - источник напряжения, управляемый током: а) нелинейный, б) линейный, γн – передаточное сопротивление

3. ИТУТ – источник тока, управляемый током: а) нелинейный, б) линейный, β - коэффициент усиления тока

4. ИТУН – источник тока, управляемый напряжением: а) нелинейный, б) линейный, S - крутизна (передаточная проводимость)

Условия эквивалентности источника напряжения и источника тока

Источник тока – это такой идеальный источник, который вырабатывает неизменную по величине силу электрического тока ( ) независимо от нагрузки.

Реальный источник тока – это такой источник, у которого внутреннее сопротивление не равно бесконечности ( ).

Докажем, что любому источнику с электродвижущей силой E и внутренним сопротивлением R_E (рис. 1.5, а) может быть найден источник тока J с тем же внутренним сопротивлением R_E (рис. 1.5, б).

Если U и I в цепях (рис. 1.5) равны, то обведенные контуром части схем эквивалентны.

Пусть сопротивления R_В в цепях (рис. 1.5) одинаковы. В цепи (рис. 1.5, а) ток можно определить по закону Ома:

.

(1.1)

В цепи (рис. 1.5, б) ток равен: . С другой стороны: , тогда

.

(1.2)

Сравнивая формулы (1.1) и (1.2), можно убедиться, что . Это и есть условие эквивалентности источников.

Значит, доказано, что реальному источнику Е, R_в всегда можно найти реальный источник тока J, R_в. Но идеальному источнику Е нельзя найти эквивалентный идеальный источник J, так как внутренние сопротивления у них не могут
быть одинаковыми (R_Е = 0, а R_J = )
Билет 12

12. Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁+ IR₂+ IR₃= I(R₁+ R₂+ R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то длярассматриваемой цепи

U = U₁+ U₂+U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁: U₂: U₃= R₁: R₂: R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

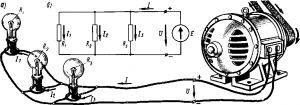Рис. 26. Схемы параллельного соединения приемников

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или

I = U / R₁+ U / R₂+ U / R₃= U (1/R₁+ 1/R₂+ 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R_эк = 1/R₁+ 1/R₂+ 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк= G₁+ G₂+G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I₁: I₂: I₃= 1/R₁: 1/R₂: 1/R₃= G₁+ G₂+ G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк= R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

Рис. 27. Схемы смешанного соединения приемников

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Определение эквивалентного сопротивления, напряжения и тока на отдельных резисторах – ДОДЕЛАТЬ111

13. Первый закон Кирхгофа (баланс токов) следует из непрерывности токов. Алгебраическая сумма токов в узле равна нулю. Закон выражает тот факт, что заряды в узле не накапливаются. Подтекающие токи берутся со знаком плюс, вытекающие со знаком минус.
Второй закон Кирхгофа (баланс напряжений). Так как любая электрическая цепь является потенциальной, то алгебраическая сумма напряжений по замкнутому контуру равна алгебраической сумме э.д.с. этого контура. Напряжения и э.д.с., совпадающие с направлением обхода, берутся со знаком плюс, иначе – со знаком минус.
.
Общее число уравнений равно числу неизвестных токов. По первому закону составляется 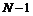уравнений, где - число узлов. Остальные уравнения - по второму закону, причем ветви с источниками токов в контура не включаются, а в каждый новый контур должна войти хотя бы одна новая ветвь.

Пример1
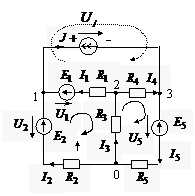
пример 1

Пример 2.

Если требуется определить напряжение между двумя любыми точками цепи, то его можно включить в контур, например, для определения напряжения на источнике тока в примере 1 составили уравнения для контура, помеченного пунктирной стрелкой:
, откуда можно определить .
Закон Ома для сложной ветви.

По второму закону Кирхгофа для контура имеем: 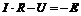, откуда . Если совпадает с направлением тока, то она берется со знаком плюс.

Закон сохранения энергии (баланс мощности) позволяет проверить правильность проведенных расчетов. Сумма мгновенных мощностей элементов цепи равна нулю: . Для примера 1: 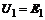. или
(баланс мощности).

Билет 14

14. Метод наложения — метод расчёта электрических цепей, основанный на предположении, что ток в каждой из ветвей электрической цепи при всех включённых генераторах, равен сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов(только в линейных цепях).

Метод наложения используется как для расчёта цепей постоянного тока, так и для расчёта цепей переменного тока.

Найти ток методом наложения в цепи, показанной на рисунке. , , .

Пример метода наложения

При отключённом генераторе 2 ток найдём по формуле:

.

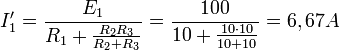При отключённом источнике 1, ток 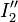будет

,

а ток будет

.

Тогда ток при обоих включённых источниках будет равен сумме токов и :

.

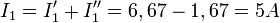В задаче за положительные направления токов и приняты направления, совпадающие с направлением, показанным на рисунке для тока . То же самое для тока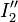

Билет 15

15. Методика расчета цепи методом контурных токов

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 Определяем все независимые контуры.

3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5 Решаем любым методом полученную систему относительно контурных токов и определяем их.

6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Не нашли, что искали? Воспользуйтесь поиском: