ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Билет 17 http://demos.hut.ru/books/electrotexnical/sloshn.html
17. Под эквивалентными преобразованиями в электрической цепи подразумевается замена одних элементов другими таким образом, чтобы электромагнитные процессы в ней не изменились, а схема упрощалась. Одним из видов таких преобразований является замена нескольких потребителей, включённых последовательно или параллельно, одним эквивалентным.
Несколько последовательно соединённых потребителей можно заменить одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых последовательно. Для n потребителей можно записать:
rэ = r1 +r2+…+rn,
где r1, r2,..., rn – сопротивления каждого из n потребителей.
При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных элементов, включённых параллельно:
gэ= g1 + g2 +…+ gn.
Учитывая, что проводимость является обратной величиной по отношению к сопротивлению, можно эквивалентное сопротивление определить из выражения:
1/rэ = 1/r1 + 1/r2 +…+ 1/rn,
где r1, r2,..., rn – сопротивления каждого из n потребителей, включённых параллельно.
В частном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи:
rэ = (r1 х r2)/(r1 + r2)
Преобразования в сложных цепях, где отсутствует в явном виде последовательное и параллельное соединение элементов (рисунок 1), начинают с замены элементов, включённых в исходной схеме треугольником, на эквивалентные элементы, соединённые звездой.

Рисунок 1. Преобразование элементов цепи: а - соединённых треугольником, б - в эквивалентную звезду
На рисунке 1, а треугольник элементов образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтобы не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений:
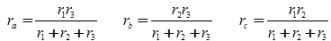
Упрощение исходной цепи можно также осуществить заменой элементов, соединённых звездой, схемой, в которой потребители соединены треугольником.
В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены между точками c, b, d. На рисунке 2, б между этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений:


Рисунок 2. Преобразование элементов цепи: а - соединённых звездой, б - в эквивалентный треугольник
Дальнейшее упрощение схем, приведённых на рисунках 1, б и 2, б, можно осуществлять путём замены участков с последовательным и параллельным соединением элементов их эквивалентными потребителями.
При практической реализации метода расчёта простой цепи с помощью преобразований выявляются в цепи участки с параллельным и последовательным соединением потребителей, а затем рассчитываются эквивалентные сопротивления этих участков.
Если в исходной цепи в явном виде нет таких участков, то, применяя описанные ранее переходы от треугольника элементов к звезде или от звезды к треугольнику, проявляют их.
Данные операции позволяют упростить цепь. Применив их несколько раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Далее, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.
Билет 18
Напряженность магнитного поля необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.
Напряженность магнитного поля (формула) векторная физическая величина, равная:

Понравился материал? расскажи друзьям о сайте физика.
Напряженность магнитного поля в СИ - ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
Величина, характеризующая способность вещества намагничиваться, называется магнитная проницаемость (µ). Она показывает, во сколько раз магнитная индукция в данном веществе больше или меньше магнитной индукции в вакууме.
Магнитная индукция в какой-либо точке поля в данной среде определяется по формуле

где B – магнитная индукция в теслах;
I – величина тока в амперах;
L – расстояние от оси провода до исследуемой точки поля в метрах;
µ — магнитная проницаемость среды.
За единицу измерения магнитной проницаемости в Международной системе единиц принят 1 генри на метр.
Магнитная проницаемость среды равна 1 гн/м, если в точке, удаленной от оси проводника с током на 1 метр, при силе тока, равной 2π ампера, магнитная индукция равна 1 тесле.
Величина магнитной проницаемости среды может быть выражена в виде произведения двух сомножителей

где µ — магнитная проницаемость среды;
µ0 – магнитная проницаемость вакуума;
µr – относительная магнитная проницаем ость, представляющая собой отвлеченное число, показывающее отношение величины магнитной проницаемости данного вещества к магнитной проницаемости вакуума.
Магнитная проницаемость вакуума µ0 в Международной системе единиц равна

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 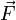 магнитное поле действует на заряд
магнитное поле действует на заряд 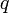 , движущийся со скоростью
, движущийся со скоростью  .
.
Более конкретно,  — это такой вектор, что сила Лоренца
— это такой вектор, что сила Лоренца 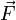 , действующая со стороны магнитного поля[1] на заряд
, действующая со стороны магнитного поля[1] на заряд 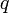 , движущийся со скоростью
, движущийся со скоростью  , равна
, равна
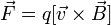
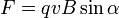
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора  перпендикулярно им обоим и направлено по правилу буравчика).
перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
Магнитное поле характеризуется также величиной, носящей название магнитного потока. Магнитный поток можно представить (если условиться изображать его графически) общим числом магнитных линий, проходящих через всю рассматриваемую поверхность. В частности, под магнитным потоком Ф, проходящим через площадь S, перпендикулярную магнитным линиям, понимают произведение величины магнитной индукции В на величину площади, которая пронизывается этим магнитным потоком.
Ф = ВS.
Билет 19
19. Если к прямолинейному проводнику с электрическим током поднести магнитную стрелку, то она будет стремиться стать перпендикулярно плоскости, проходящей через ось проводника и центр вращения стрелки. Это указывает на то, что на стрелку действуют особые силы, которые называются магнитными силами. Кроме действия на магнитную стрелку, магнитное поле оказывает влияние на движущиеся заряженные частицы и на проводники с током, находящиеся в магнитном поле. В проводниках, движущихся в магнитном поле, или в неподвижных проводниках, находящихся в переменном магнитном поле, возникает индуктивная эдс.
Вокруг проводника с током образуется магнитное поле, так что свободно вращающаяся магнитная стрелка, помещенная вблизи проводника, будет стремиться занять положение, перпендикулярное плоскости, проходящей вдоль него.
В этом легко убедиться, проделав следующий опыт.
Магнитное поле
прямого проводника с током
В отверстие горизонтально положенного листа картона вставляют прямолинейный проводник и пропускают через него ток. Насыпают на картон железные опилки и убеждаются в том, что они располагаются концентрическими окружностями, имеющими общий центр в точке пересечения проводником картонного листа.
Магнитная стрелка, подвешенная на нити вблизи этого проводника, займет положение, указанное на рисунке. При изменении направления тока в проводнике магнитная стрелка повернется на угол 180°, оставаясь в положении, перпендикулярном плоскости, проходящей вдоль проводника.
В зависимости от направления тока в проводнике направление магнитных линий образуемого им магнитного поля определяется правилом буравчика, которое формулируется следующим образом:
Если поступательное движение буравчика совпадает с направлением тока в проводнике, то вращательное движение его рукоятки указывает направление магнитных линий поля, образующегося вокруг этого проводника.
Если по проволоке, согнутой в виде кольца, пропустить ток, то под действием его также возникнет магнитное поле.
Билет 20
20. Магнитное поле катушки с током возникает в кольцевой катушке с W витками, равномерно распределенными вдоль немагнитного сердечника при подключении ее к источнику тока. Увеличение магнитной индукции поля достигается увеличением числа витков катушки и размещением ее на стальном сердечнике, магнитные токи которого, создавая свое поле, увеличивают результирующее поле катушки. Поверхность, ограниченная окружностью радиуса R, совпадающей со средней магнитной линией, пронизывается полным током ΣI = IW. Вследствие симметрии напряженность поля Н во всех точках, лежащих на средней магнитной линии, одинакова, поэтому мдс Fм = Hl = IW = H2πR. По закону полного тока Hl = IW, откуда напряженность магнитного поля на средней магнитной линии, совпадающей с осевой линией кольцевой катушки, H = IW / l, а магнитная индукция B = μaH = μaIW / l = 125μIW / l * 10-8.
При R1 - R2 << Rl магнитную индукцию на осевой линии с достаточной точностью можно считать равной среднему значению ее, и, следовательно, магнитный поток сквозь поперечное сечение катушки Φ = BS = μaIWS / l. Переписав это уравнение в виде Φ = IW / (μaSl) = Fм / Rм, получим выражение, аналогичное уравнению закона Ома для электрической цепи, т. е. полный магнитный поток равен отношению мдс к магнитному сопротивлению цепи. Цилиндрическую катушку можно рассматривать как часть кольцевой катушки с большим радиусом и с обмоткой, расположенной только на части сердечника, длина которой равна длине катушки. Напряженность поля и магнитной индукции на осевой линии в центре цилиндрической катушки определяется по формулам, которые в этом случае являются приближенными и применимы для катушек.
В 1600 году английский ученый Уильям Гильберт в своей книге «О магните, магнитных телах
и большом магните - Земле». представил Землю, как гигантский постоянный магнит, ось которого
не совпадает с осью вращения Земли (угол между этими осями называют магнитным склонением).
Гильберт подтвердил свое предположение на опыте:
он выточил из естественного магнита большой шар и, приближая к поверхности шара магнитную стрелку, показал, что она всегда устанавливается так же, как стрелка компаса на 3емле.
Графически магнитное поле Земли похоже на магнитное поле постоянного магнита.
В 1702 году Э. Галлей создает первые магнитные карты Земли.
___
Основная причина наличия магнитного поля Земли в том, что ядро Земли состоит из раскаленного железа (хорошего проводника электрических токов, возникающих внутри Земли).
___
Магнитное поле Земли образует магнитосферу, простирающуюся на 70-80 тыс. км
в направление Солнца. Она экранирует поверхность Земли, защищает от вредного влияния
заряженных частиц, высоких энергий и космических лучей, определяет характер погоды.
Внутри кинескопа магнитное поле оказывает действие на поток электронов, движущихся в вакууме. Если электроны будут двигаться не в вакууме, а внутри проводника, создавая внутри его ток, то действие магнитного поля сохранится.Магнитное поле будет действовать на электроны, а те - на ионы проводника, внутри которого они движутся. В результате этого появится сила, приложенная ко всему проводнику с током.
Убедимся в этом на опыте. Соберем электрическую цепь, изображенную на рисунке 66, а. Замкнув цепь, мы увидим, как проводник AВ, подвешенный между полюсами магнита, придет в движение и установится в положении, изображенном на рисунке 66, б. Причиной смещения проводника является действие, оказываемое на него магнитным полем постоянного магнита.
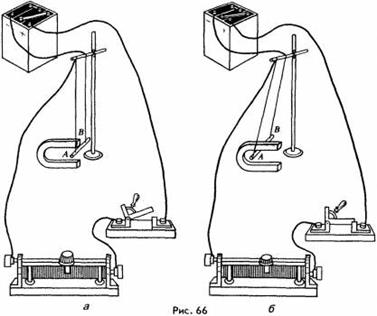
Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера.
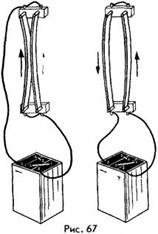
Французский физик А. М. Ампер был первым, кто обнаружил действие магнитного поля на проводник с током. Правда, источником магнитного поля в его опытах был не магнит, а другой проводник с током. Помещая проводники с током рядом друг с другом, он обнаружил магнитное взаимодействие токов (рис. 67) - притяжение параллельных токов и отталкивание антипараллельных (т. е. текущих в противоположных направлениях). В опытах Ампера магнитное поле первого проводника действовало на второй проводник, а магнитное поле второго проводника - на первый. В случае параллельных токов силы Ампера оказывались направленными навстречу друг другу и проводники притягивались; в случае антипараллельных токов силы Ампера изменяли свое направление и проводники отталкивались друг от друга.
Направление силы Ампера можно определить с помощью правила левой руки:
если расположить левую ладонь руки так, чтобы четыре вытянутых пальца указывали направление тока в проводнике, а силовые линии магнитного поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник с током (рис. 68).
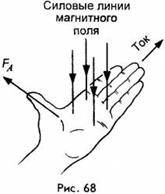
Эта сила (сила Ампера) всегда перпендикулярна проводнику, а также силовым линиям магнитного поля, в котором этот проводник находится.
Сила Ампера действует не при любой ориентации проводника. Если проводник с током расположить вдоль силовых линий магнитного поля, то это поле никакого действия на него не окажет.
Билет 21
21. Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину
|
где B – модуль вектора магнитной индукции, α – угол между вектором 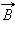 и нормалью
и нормалью 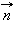 к плоскости контура (рис. 1.20.1).
к плоскости контура (рис. 1.20.1).

|
Рисунок 1.20.1.
Магнитный поток через замкнутый контур. Направление нормали 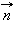 и выбранное положительное направление и выбранное положительное направление 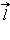 обхода контура связаны правилом правого буравчика обхода контура связаны правилом правого буравчика
|
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
| 1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции 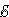 инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
|
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Индуктированная э. д. с. возникает в следующих трех случаях:
когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;
когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем э. д. с. (взаимоиндукция);
когда изменяющееся магнитное поле какого-либо проводника индуктирует в нем самом э. д. с. (самоиндукция).
Таким образом, всякое изменение во времени величины магнитного потока (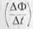 ), пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е:
), пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е:
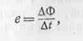
где ΔФ — магнитный поток, пересеченный проводником за промежуток времени Δt.
Величина индуктированной э. д. с. в проводнике зависит: от величины индукции В магнитного поля, так как чем плотнее Расположены магнитные линии, тем большее число их пересечет проводник за единицу времени (секунду);
скорости движения проводника V в магнитном поле, так как при большей скорости движения проводник может больше пересечь магнитных линий в секунду;
от активной (находящейся в магнитном поле) длины проводника, так как длинный проводник может больше пересечь магнитных линий в секунду;
от величины синуса угла а между направлением движения проводника и направлением магнитного поля (рис. 93).
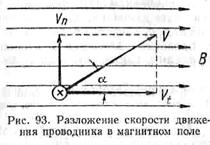
Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: Vн — составляющую, нормальную к направлению поля (Vн = V sin α), и V, — тангенциальную составляющую (Vt = V cos α), которая не принимает участия в создании з. д. с, так как при движении под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору В и не пересекал бы линий магнитной индукции.
Величина индуктированной э. д. с. может быть найдена по формуле
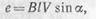
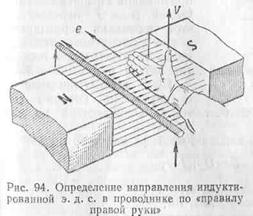
где В — величина магнитной индукции, тл; l — активная длина проводника, м;
V — скорость движения проводника, м/сек;
α— угол пересечения. Как было отмечено выше, направление индуктированной э. д. с. зависит от направления движения проводника и от направления магнитного поля.
Для определения направления индуктированной э. д. с. в проводнике, движущемся в магнитном поле, служит «правило правой руки». Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут показывать направление э. д. с, индуктированной в проводнике (рис. 94).
В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной э. д. с. следует предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить также «правило правой руки».
Билет 22
22. ЭДС индукции, наведённая в контуре – ДОДЕЛАТЬ111
В 1834 г. русский академик Э. X. Ленц, известный своими многочисленными исследованиями в области электромагнитных явлений, дал универсальное правило для определения направления индуктированной э. д. с. в проводнике. Это правило, известное как правило Ленца, может быть сформулировано так:
направление индуктированной э. д. с. всегда таково, что вызванный ею ток и его магнитное поле имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктированную э. д. с
С учетом этого правила можно закон электромагнитной индукции выразить более общей формулой, позволяющей определить не только величину, но и направление индуктированной э. д. с:

Выражение 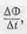 представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени ∆t, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.
представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени ∆t, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.
Знак минус, стоящий перед выражением 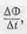 , определяет направление индуктированной э. д. с, т. е. учитывает правило Ленца.
, определяет направление индуктированной э. д. с, т. е. учитывает правило Ленца.
При увеличении магнитного потока выражение 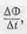 будет положительным, а э. д. с. — отрицательной. В этом и заключается правило Ленца: э. д. с. и созданный ею ток противодействуют причине, которая их вызвала.
будет положительным, а э. д. с. — отрицательной. В этом и заключается правило Ленца: э. д. с. и созданный ею ток противодействуют причине, которая их вызвала.
При равномерном изменении во времени магнитного потока выражение 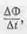 будет постоянно. Тогда абсолютное значение э. д. с. в проводнике будет равно
будет постоянно. Тогда абсолютное значение э. д. с. в проводнике будет равно

Если катушка состоит из w витков, соединенных между собой последовательно, то индуктированная э. д. с. в ней равняется сумме э. д. с, индуктированных в отдельных витках:
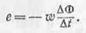
ЭДС индукции в катушке – ДОДЕЛАТЬ111
Потокосцепление — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности.
Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как 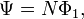 где
где 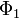 — магнитный поток одного витка
— магнитный поток одного витка
Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как 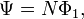 где
где 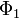 — магнитный поток одного витка
— магнитный поток одного витка
В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:
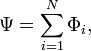
где:
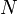 — количество витков;
— количество витков;
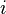 — номер витка, с которым сцеплен поток
— номер витка, с которым сцеплен поток 
В случае, если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:
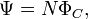
где 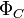 — магнитный поток через магнитопровод (сердечник) катушки.
— магнитный поток через магнитопровод (сердечник) катушки.
Величина потокосцепления, помимо магнитного потока, имеет связь с током I в индуктивности, определяющуюся выражением:

где  — индуктивность катушки [ Гн ].
— индуктивность катушки [ Гн ].
Эта формула выражает принцип непрерывности во времени потокосцепления катушки индуктивности.
Билет 23
Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
Не нашли, что искали? Воспользуйтесь поиском: