
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Раздел 1. Элементы теории пределов
I. Задания для самостоятельной работы
1. Изучить теоретический материал по теме «Предел и непрерывность функции» по вопросам:
1.1. Бесконечно малые в точке функции, их свойства.
1.2. Сравнение бесконечно малых.
1.3. Предел функции в точке.
1.4. Предел функции на бесконечности.
1.5. Свойства пределов.
1.6. Эквивалентные функции.
1.7. Методы раскрытия неопределенности при вычислении пределов.
2. Выполнить задания:
Задача 1. Найти пределы функций, не используя правило Лопиталя.
1) 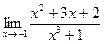 2)
2)  3)
3) 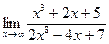 4)
4) 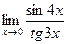 5)
5) 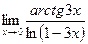 11)
11) 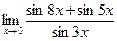 12)
12) 
| 6) 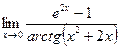 7)
7) 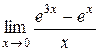 8)
8) 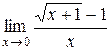 9)
9) 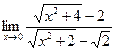 10)
10)  13)
13)  14)
14) 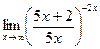
|
Задача 2. Исследовать функции на непрерывность. Указать точки разрыва и характер разрыва.
1) 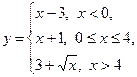 ; 2)
; 2)  ;
;
3) 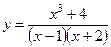 ; 4)
; 4) 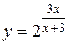
II. Контрольные вопросы для самопроверки
1. Что такое функция?
2. Какая функция называется бесконечно малой при х ® а?
3. Какие основные свойства бесконечно-малых функций вы знаете?
4. Что такое предел функции в точке?
5. Сформулируйте основные теоремы о пределах.
6. Какая функция называется непрерывной в точке?
7. В чем заключается первый замечательный предел?
8. Какие бесконечно малые функции называются эквивалентными?
Не нашли, что искали? Воспользуйтесь поиском: