Метод аналитического выравнивания

Выявление общей тенденции развития уровней динамического ряда может быть проведено с применением различных приемов аналитического выравнивания, которое наиболее часто осуществляется следующими способами: во-первых, выравниванием по прямой линии; во- вторых, по показательной кривой; в-третьих, по гиперболе; в-четвертых, по параболе второго порядка.

При выравнивании по прямой линии закономерно изменяющиеся уровни динамического ряда рассчитываются как функция времени, выражающаяся уравнением: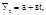

где – выровненные значения уровней ряда; t – периоды или моменты времени, к которым относятся уровни; а, в – параметры уравнения (искомой прямой).

Для расчета параметров уравнения прямой линии рекомендуется применять способ наименьших квадратов, в основе которого лежит следующие требование: сумма квадратов отклонений фактических уровней ряда (У) от выровненных и лежащих на искомой линии теоретических уровней должна иметь минимальное значение, т.е.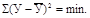

Этому требованию удовлетворяет система нормальных уравнений, которые в соответствии с обозначениями формулы (16) могут быть записаны следующим образом

где У – значения фактических уровней ряда динамики; t – порядковые номера периодов или моментов времени; n – число фактических уровней динамического ряда.

Приведенную систему нормальных уравнений можно упростить, если срединный уровень ряда условно принять на начальный. В этом случае Σt=0, а система уравнений примет следующий вид:

откуда параметры а, в выразят так:

,

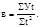
Определив параметры а, в, легко найти выравненные значения уровней и изобразить их графически в виде теоретической прямой линии.

Параметр a в линейной трендовой модели обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда.

Параметр b в трендовом уравнении называется коэффициентом регрессии. Он определяет направление развития явления: при b >0 – уровни ряда динамики равномерно возрастают, при b <0 – равномерно снижаются. Коэффициент регрес-сии показывает, насколько в среднем изменится уровень ряда при изменении времени на единицу. Это означает, что параметр b можно рассматривать как средний абсолютный прирост с учетом тенденции к равномерному росту (росту в ариф-метической прогрессии).

Полученные при анализе динамических рядов характеристики используются для получения статистических прогнозов, под которыми I II III IV понимаются статистические оценки состояния явления в будущих периодах.

Метод прогнозирования на основе среднего абсолютного прироста Δ применяется в том случае, если уровни изменяются равномерно (линейно).

Так, если фактические уровни динамического ряда характеризуются более-менее стабильными (положительными или отрицательными) абсолютными приростами и на координатной диаграмме они равномерно отклоняются от теоретической прямой линии, то выравнивание уровней может проводиться по среднему абсолютному приросту, т.е.

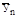где – выравниваемый искомый уровень; У0 – начальный (базисный) уровень; 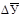– средний абсолютный прирост уровней ряда; n – порядковый номер искомого (выравниваемого) уровня.

Прогнозирование по среднему коэффициенту роста K применяется, если общая тенденция характеризуется экспотенциальной кривой.

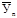В тех случаях, когда изучаемый динамический ряд характеризуется более-менее стабильными повышающимися или снижающимися темпами роста, выравнивание уровней такого ряда можно проводить с помощью среднего коэффициента (темпа) роста: где – выравниваемый искомый уровень;

У0 – начальный уровень ряда;

– средний коэффициент роста уровней;

n – порядковый номер выравниваемого уровня

Не нашли, что искали? Воспользуйтесь поиском: