
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
1 страница. (4.18) формуласы потенциалды өрістегі энергия мен күштің арасындағы байланысты өрнектейді.
Немесе
 . (4.18)
. (4.18)
(4.18) формуласы потенциалды өрістегі энергия мен күштің арасындағы байланысты өрнектейді.
9. Қозғалмайтын О нүктесіне қатысты Ғ күшінің моменті деп О нүктесінен күштің А түсу нүктесіне жүргізілген  радиус-вектор мен Ғ күштің векторлық көбейтіндісімен анықталатын физикалық шама:
радиус-вектор мен Ғ күштің векторлық көбейтіндісімен анықталатын физикалық шама:
 . (3.1)
. (3.1)

|
Сурет
Күш моменті күштің денені нүктеге қатысты айналдыру қабілетін сипаттайды. О нүктесіне бекітілген дене  күштің әсерінен
күштің әсерінен  моменттің бағытымен сәйкес келетін осьті айналады (3.1 суретті қара).
моменттің бағытымен сәйкес келетін осьті айналады (3.1 суретті қара).
Бөлшектің О нүктесіне қатысты импульс моменті деп О нүктесінен күштің А түсу нүктесіне жүргізілген  радиус-вектор мен Р импульстың векторлық көбейтіндісіне
радиус-вектор мен Р импульстың векторлық көбейтіндісіне
 , (3.2)
, (3.2)
тең шаманы айтады,
мұндағы  – берілген уақыт мезетіндегі бөлшектің радиус-векторы;
– берілген уақыт мезетіндегі бөлшектің радиус-векторы;
 – оның импульсі (
– оның импульсі (  ).
).
Импульс моментінің векторы  және
және  векторлары жатқан жазықтыққа
векторлары жатқан жазықтыққа

Сурет
перпендикуляр болады (3.2 суретті қара).
10. Айналмалы қозғалыс динамикасының негізгі заңын қорытқан кезде, біз қатты денені материялық нүктелер жиынтығы деп қарастырып, мынадай қорытындыға келдік
 , (5.2)
, (5.2)
мұндағы  –жүйенің импульс моменті;
–жүйенің импульс моменті;  – жүйеге әсер ететін сыртқы күштердің қорытқы моменті.
– жүйеге әсер ететін сыртқы күштердің қорытқы моменті.
Ішкі күштердің моменттерінің қосындысы кез келген жүйе үшін нөлге тең.
Егер сыртқы күштер болмаса (тұйықталған жүйеде), онда  , сондықтан,
, сондықтан,  .
.
 (5.3)
(5.3)
Тұйықталған жүйенің материялық нүктелерінің (денелер) толық импульс моменті тұрақты болып қалады.
Егер дене қозғалмайтын осьті айналып қозғалса,  , онда
, онда  .
.  екенін ескерсек,
екенін ескерсек,
 . (5.4)
. (5.4)
Импульс моментінің сақталу заңы да импульстің сақталу заңы сияқты табиғаттың негізгі заңы болып табылады. Оның негізінде кеңістіктің изотроптылығы қасиеті жатыр, яғни тұйық жүйенің бұрылуы оның механикалық қасиеттеріне әсер етпейді.
11. Күш жұмысы және оның қисық сызықты интеграл арқылы өрнектелуі. Қуат
Массасы m қандай да бір бөлшекті қарастырайық. Оған 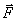 күшпен әсер етейік. Осы бөлшек үшін Ньютонның екінші заңының теңдеуі
күшпен әсер етейік. Осы бөлшек үшін Ньютонның екінші заңының теңдеуі
 (1)
(1)
(1) теңдеуін бөлшектің шексіз аз  орын ауыстыру векторына көбейтсек (=
орын ауыстыру векторына көбейтсек (=  екенін ескереміз)
екенін ескереміз)
 (2)
(2)
1 суреттен  скаляр көбейтіндісі
скаляр көбейтіндісі

тең болады.

Сурет
Онда,
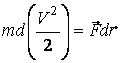 . (3)
. (3)
(3) –тің оң жағындағы шама күштің dA жұмысы деп аталады.
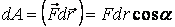 , (4)
, (4)
мұндағы α – күш пен  орын ауыстырудың арасындағы бұрыш.
орын ауыстырудың арасындағы бұрыш.
(4) формуласы күштің элементар жұмысын сипаттайды. Дене шекті қашықтыққа орын ауыстырғанда атқарылатын толық жұмыс қозғалыс траекториясы бойымен алынған қисық сызықты интеграл бойынша анықталады.
 . (5)
. (5)
Күш жұмысы – алгебралық шама, ол оң да, теріс те, нөлге де тең болуы мүмкін. Жұмыстың графиктік түрде анықталуы 2 суретте көрсетілген.

Сурет
Дененің M0M1 сызығы бойымен шекті орын ауыстыруы кезіндегі күштің Жұмысы (А), қисық сызықты интеграл арқылы, элементар Ж-тардың интегралдық қосындысы ретінде анықталады.
Қуат - уақыт бірлігі ішінде істелінген жұмыстың сол уақытқа қатынасымен өлшенетін физикалық шама.
Бірқалыпты жұмыс істейтін жүйе үшін қуат: N=А/t өрнегі бойынша есептеледі, мұндағы А – t уақыт ішінде істелетін жұмыс, жалпы жағдайда лездік қуат -
 ,
,
dA – элементар уақыт бірлігі (dt) ішіндегі элементар жұмыс.
Дененің қозғалыс бағытымен әсер ететін тұрақты күштің қуатын:

өрнегімен де анықтауға болады, мұндағы F – денеге әсер ететін күш, V – дененің жылдамдығы.
Электр қуатының лездік мәні

формуласымен есептеледі.
Реактивті қуат - электротехникалық құрылғылардағы электромагниттік өріс энергиясынын тербелісі жасайтын жүктемені сипаттайтын шама.
Қуаттың бірліктердің халықаралық жүйесіндегі (СИ) өлшем бірлігі – Ватт (Вт). Вт=Дж/с. Қуаттың еселі өлшемдері:1 кВт=103Вт, 1 МВт=106Вт техникада кеңінен қолданылады; сонымен қатар Қуат бірлігі ретінде ат күші (а. к.) де қолданылады, 1 а.к.=735,5Вт.
12. Денелердің тұйық жүйесі. Импульстің сақталу заңы. Абсолют серпімді және серпімсіз соққылар.
Денелердің тұйық жүйесі
Механикалық жүйе сыртқы депнелермен өзара әсерлеспесе (немесе оған сыртқы күштер әсер етпесе), онда ол тұйықталған немесе оқшауланған жүйе деп аталады
Материялық нүктелердің (денелердің) бір –біріне әсері өзара әсерлесу сипатта болады.
Ньютонның үшінші заңы: Материялық нүктелердің бір-біріне әсер ету күштері модулі бойынша әрқашан тең, бағыты жағынан қарама-қарсы және осы нүктелерді қосатын түзу бойымен әсер етеді: Ғ1,2 = - F2,1.
Бұл күштер әр материялық нүктеге түсірілгені, әрқашан жұбымен әсерлеседі және табиғаты бір болып табылады. Ньютонның үшінші заңы жеке материялық нүктелер динамикасынан кезкелген материялық нүктелер жүйесі динамикасына өтуге мүмкіндік береді, үйткені кезкелген өзара әсерлесуді материялық нүктелердің жұпталып өзара әсерлесуі ретінде қарастыруға болады.
Импульстің сақталу заңы
P1+P2=P1́+P2́- теңдік өзара әрекеттескенге дейінгі жүйе импульсі өзара әрекеттескеннен кейінгі жүйе импульсіне тең.
Бұл- импульстің сақталу заңы және ол былайша оқылады:тұйық жүйеде өзара әрекеттесетін денелер импульстерінің векторлық қосындысы өзгеріссіз қалады(сақталады)
Импульстің сақталу заңы біз қарастырып отырған денелер жүйесіне сырттан ешқандай күштер әрекет етпесе ғана орындалады.
Денелердің механикалық энергиясы энергияның басқа түріне айналмаған соқтығысуды абсолют серпімді соқтығысу деп атайды.
Абсолют серпімді соқтығысуда импульстің және механикалық энергияның сақталу заңдары орындалады.
Массалары m1 және m2 шарлардың соқтығысқанға дейінгі жылдамдықтарын v1 және v2, ал соқтығысқаннан кейінгі жылдамдықтарын v'1 және v'2 деп белгілейік (8-сурет). Түзу орталық соққы кезінде шарлардың жылдамдық векторлары соққыға дейін және кейін олардың центрлерін қосатын түзудің бойында жатады. Олардың бағыттарын таңбаларымен ескереміз: оң таңбаңы оңға қарай бағыттаймыз, теріс таңбаны солға қарай бағыттаймыз.
 m1 m2
m1 m2
v1 v2
m1 m2
v' 1 v' 2
Сурет 9-сурет
Осы бойынша сақталу заңдары келесі түрде жазылады
m1 v1 + m2 v2 = m1 v' 1 + m2 v' 2 (4.1)
(m1v21)/2+(m2v22)/2=(m1v1'2)/2+(m2v2'2) (4.2)
(4.1) және (4.2) өрнектерін түрлендіруден кейін келесі өрнектерді аламыз:
m1(v1-v'1)=m2(v2' -v2) (4.3) m1(v21-v'21)=m2(v2'2–v22) (4.4)
осыдан v1+v'1=v2'+v2 (4.5)
(4.3) және (4.5) теңдіктерді шеше отырып, келесі шамаларды табамыз
v'1=((m1– m2) v1+2 m2 v2)/ (m1+m2) (4.6)
v'2 =((m2–m1)v2+2 m1v1)/ (m1+m2) (4.7)
Абсолют серпімсіз соққы. Абсолют серпімсіз соққы -соққы нәтижесінде екі дене тұтас дене сияқты бірге қозғалады. Абсолют серпімсіз соққыны көрсету үшін бір-біріне қарама-қарсы келе жатқан екі шардың қозғалысын қарастырамыз (12-сурет).
m1 v1 m2 v2=0 m1 v1 m2 v2=0

m1 v,1 m2 v,2
v,1 m1 m2 v,2
Сурет 11-сурет
Егер шарлардың m1 және m2, ал соқтығысқанға дейінгі жылдамдықтары v1 және v2 болса, онда импульстің сақталу заңын қолданып, келесі өрнекті жазуға болады m1 v1+m2v2 =(m1+m2)v (4.10)
осыдан v=(m1v1 + m2 v2)/ (m1+m2) (4.11)
13. Айналу осіне қатысты дененің импульс моменті. Импульс моментінің сақталу заңы. Мысалдар.
Массасы  қатты дененің кішкентай бөлшегін қарастырайық. Оның жылдамдығы
қатты дененің кішкентай бөлшегін қарастырайық. Оның жылдамдығы  және оған қатысты импульсі
және оған қатысты импульсі  нүкте траекториясына жанама бойымен бағытталған.
нүкте траекториясына жанама бойымен бағытталған.
 4.2-сурет.Импульс моментін анықтау
4.2-сурет.Импульс моментін анықтау
| Қозғалмайтын О нүктесіне қатысты импульс моменті векторы  материялық нүктенің радиус-векторы материялық нүктенің радиус-векторы  мен оның импульсінің мен оның импульсінің  векторлық көбейтіндісіне тең физикалық шама: векторлық көбейтіндісіне тең физикалық шама:
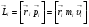 . (4.5)
Импульс моменті векторы . (4.5)
Импульс моменті векторы  векторлық көбейтінді ережесі арқылы анықталып, айналу осі бойында жатады, ал оның модулі мына өрнекпен анықталады: векторлық көбейтінді ережесі арқылы анықталып, айналу осі бойында жатады, ал оның модулі мына өрнекпен анықталады:
 (4.6) (4.6)
|
Материялық нүктенің  осіне қатысты импульс моменті векторы
осіне қатысты импульс моменті векторы  осы
осы  векторының айналу осіне түсірілген проекциясы арқылы анықталады. Ол айналу осінде жатыр және оның модулі мына теңдеу арқылы анықталады.
векторының айналу осіне түсірілген проекциясы арқылы анықталады. Ол айналу осінде жатыр және оның модулі мына теңдеу арқылы анықталады.
 (4.7)
(4.7)
Қатты дененің  осьіне қатысты
осьіне қатысты  импульс моменті векторы барлық нүктелерінің
импульс моменті векторы барлық нүктелерінің  векторларының қосындысына тең. Барлық векторлар айналу осінде жатыр және бірдей бағытталған.Олардың модулі мынаған тең.
векторларының қосындысына тең. Барлық векторлар айналу осінде жатыр және бірдей бағытталған.Олардың модулі мынаған тең.
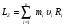
 (4.8)
(4.8)
(4.8) теңдігін векторлық түрде былай жазуға болады:
 . (4.9)
. (4.9)
(4.9) уақыт бойынша дифференциалдап ( ) (4.4) мына өрнекті аламыз:
) (4.4) мына өрнекті аламыз:

 . (4.10)
. (4.10)
Бұл қатты дененің айналмалы қозғалыс динамикасының негізгі заңының бір түрі: ось бойымен қатты дененің айналу кезіндегі импульс моменті  уақыт бойынша туындысы сол денеге әсер ететін сыртқы күштердің моментіне (
уақыт бойынша туындысы сол денеге әсер ететін сыртқы күштердің моментіне ( ) тең.
) тең.
Соңғы теңдікті былай жазуға болады.
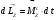 (4.11)
(4.11)
Айналушы дененің импульс моментінің өзгерісі оған әсер етуші сыртқы күштердің әсерінен болады.
Тұйық жүйеде сыртқы күштердің моменті  нольге тең.
нольге тең.
 және
және  (4.12)
(4.12)
Бұл теңдік импульс моментінің сақталу заңын құрайды: қозғалмайтын оське қатысты дененің импульс моменті тұйық жүйеде тұрақты болып, уақыт бойынша өзгермейді.
Бұл тұжырым табиғаттың іргелі заңдарының бірі болып, кеңістіктің изотропты (барлық бағыттар тең құқықты) екендігінің салдары, яғни табиғатта оқшауланған бағыттың жоқ екендігін көрсетеді. Тұйық жүйенің бұрылуы оның механикалық қасиеттерін өзгерте алмайды.
 , онда тұйық жүйе үшін теңдік
, онда тұйық жүйе үшін теңдік 
 (4.13)
(4.13)
Егер дененің инерция моменті өзгермейтін болса, онда дене тұрақты бұрыштық жылдамдықпен қозғалыс жасайды ( ), (
), ( ). Егер
). Егер  шамасы өзгерсе, онда
шамасы өзгерсе, онда 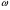 шамасы да өзгереді. Егер
шамасы да өзгереді. Егер  артса, онда
артса, онда 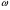 азаяды.
азаяды.
Импульс моментінің сақталу заңын Жуковскийдің тәжірибесінен көз жеткізуге болады (4.3-сурет).
14. Бөлшектің және бөлшектер жүйесінің кинетикалық энергиясы. Кинетикалық энергияның жұмыспен байланысы. Қатты дененің айналмалы қозғалысы кезіндегі кинетикалық энергия мен жұмыс. Жазық қозғалыс кезіндегі қатты дененің кинетикалық энергиясы.

теңдеуінің сол жағын қарастырайық. Ол қандай да бір функцияның толық дифференциалын береді.
. (4.7)
Wk шамасы бөлшектің кинетикалық энергиясы деп аталады. Кинетикалық энергия – толық энергияның бөлшектің қозғалысымен байланысты бөлігі. Тыныштықта тұрған дененің (V =0) кинетикалық энергиясы болмайтынын ескерсек, (4.7)-дан  тең екені шығады.
тең екені шығады.
Қозғалмайтын осьті айналып қозғалған қатты дененің айналмалы қозғалысы кезіндегі кинетикалық энергиясы  . (4.9)
. (4.9)
(4.8) және (4.9) өрнектері релятивистік емес (v<< c) бөлшектер үшін дұрыс болады. (4.8) өрнегі бөлшекке бірнеше күш әсер еткен жағдайда да дұрыс болып табылады. Онда А12 - барлық күштердің жұмыстарының қосындысы. Олай болса, бөлшектің кинетикалық энергиясының өзгерісі осы бөлшекке әсер етуші барлық күштердің жұмысына тең болады. А12=Wk2-Wk1. (4.10)
Дене Ғ күштің әсерімен dφ аз бұрышқа бұрылғанда күштің түсу нүктесі ds= r dφ жол жүреді де істелген жұмыс dA = F sin φ r dφ = Mz dφ.
15. Бөлшектің және бөлшектер жүйесінің толық механикалық энергиясы. Механикалық энергияның сақталу заңы. Энергияның сақталу және айналу заңы.
Инерциалды санақ жүйесі. Салыстырмалылықтың механикалық принципі және Галилей түрлендірулері. Ньютон механикасындағы жылдамдықтарды қосу заңы.
Бөлшектің және бөлшектер жүйесінің толық механикалық энергиясы. Механикалық энергияның сақталу заңы. Энергияның сақталу және айналу заңы.
Энергияның сақталу және айналу заңы табиғаттың негізгі заңдарының бірі болып табылады. Энергияның сақталу заңы уақыттың біртектілігін көрсетеді, яғни уақыттың барлық кезеңдері үшін бірдей. Уақыттың әр кезеңдерінің эквивалентті болу себебі кез келген физикалық процесс оның қашан басталғанына тәуелсіз бірдей жүріп отырады. Энергияның сақталу және айналу заңының терең мағынасы бар. Ол қозғалыстың материяның ажырамас қасиеті екенін, оның пайда болмайтынын және жоғалмайтынын, бір түрден екінші түрге айналатынын көрсетеді.
Бөлшек пен бөлшектер жүйесінің толық механикалық энергиясын қарастырайық. (4.7) формуласына оралайық. Бөлшекке консервативті  және консервативті емес
және консервативті емес  күштер әсер етеді делік. Онда Wk2–Wk1=A12*+A12 A12*=Wp1–Wp2 екенін ескерсек, (Wk2+Wp2)–(Wk1+Wp1)=A12 (5.5)
күштер әсер етеді делік. Онда Wk2–Wk1=A12*+A12 A12*=Wp1–Wp2 екенін ескерсек, (Wk2+Wp2)–(Wk1+Wp1)=A12 (5.5)
Бөлшектің толық механикалық энергиясы W кинетикалық және потенциалдық энергияларының қосындысына тең. Консервативті күш өрісіндегі бөлшектің толық механикалық энергиясының өзгерісі бөлшекке әсер ететін консервативті емес күштердің жұмысына тең W2–W1=A12 . (5.6)
N өзара әсерлеспейтін бөлшектер жүйесінің энергиясы осы жүйені құрайтын бөлшектердің барлық энергияларының қосындысымен анықталады  . (5.7)
. (5.7)
Егер бөлшектер бір-бірімен өзара әсерлесетін болса, аддитивті болып табылмайтын олардың өзара әсерлесу энергиясын ескеру қажет.  .(5.8)
.(5.8)
Егер жүйе бөлшектерінің арасында сыртқы күштер болмай (A12 =0), тек қана консервативті күштер әсер етсе (мұндай жүйені консервативті деп атайды), (5.7) формуладан көретініміздей, оның толық механикалық энергиясы сақталып қалады. Бұл тұжырым толық механикалық энергияның сақталу заңы болып табылады. Толық механикалық энергия тек денелердің тұйықталған консервативті жүйесінде ғана сақталады.
Не нашли, что искали? Воспользуйтесь поиском: