
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
4 страница. Қозғалмайтын электр зарядтарының электр өрісі электростатикалық өріс деп аталады
Қозғалмайтын электр зарядтарының электр өрісі электростатикалық өріс деп аталады. Электр өрісінің кернеулігі – векторлық шама, өрстің берілген нүктедегі бірлік сыншы  зарядқа әсер ететін күш:
зарядқа әсер ететін күш:  .
.  векторының бағыты оң зарядқа әсер ететін күштің бағытымен анықталады.. Кулон заңы – вакуумде нүктелік екі зарядтың өзара әсерлесу күші әр бір зарядтардың шамаларына тура пропорционал, ал ара қашықтығының квадратына кері пропорционал болып, зарядтар арқылы өтетін түзумен бағытталады:
векторының бағыты оң зарядқа әсер ететін күштің бағытымен анықталады.. Кулон заңы – вакуумде нүктелік екі зарядтың өзара әсерлесу күші әр бір зарядтардың шамаларына тура пропорционал, ал ара қашықтығының квадратына кері пропорционал болып, зарядтар арқылы өтетін түзумен бағытталады:  .
.  , мұнд.
, мұнд.  . Зарядталған бөлшектер бір-бірімен өріс арқылы әсерлеседі. Қозғалмайтын электр зарядтарының электр өрісі электростатикалық өріс деп аталады. Электр өрісінің кернеулігі – векторлық шама, өрстің берілген нүктедегі бірлік сыншы
. Зарядталған бөлшектер бір-бірімен өріс арқылы әсерлеседі. Қозғалмайтын электр зарядтарының электр өрісі электростатикалық өріс деп аталады. Электр өрісінің кернеулігі – векторлық шама, өрстің берілген нүктедегі бірлік сыншы  зарядқа әсер ететін күш:
зарядқа әсер ететін күш:  .
.  векторының бағыты оң зарядқа әсер ететін күштің бағытымен анықталады.
векторының бағыты оң зарядқа әсер ететін күштің бағытымен анықталады.
31.Электростатикалық өріс. Нүктелік зарядтың өрісінің кернеулігі және потенциалы. Электр өрістерінің суперпозиция принципі.
Электр өрісі – электр зарядтары өзара әсерлесетін материяның түрі. Электр өрісін заряд туғызады. Қозғалмайтын заряд өрісін – электростатикалық деп атайды. Элекр өрісін өлшеуіш құралдармен байқауға болады. Осы сыншы зарядты электр өрісіне қойған кезде оң зарядтардың кеңістіктегі орнына және мәніне ешбір өзгеріс енгізбеу керек. Осыған қандайда бір F күші әсер етсін делік. Осы күштің сынақ зарядқа қатынасының векторлық шамасы электр өрісінің кернеулігі деп аталды. Зарядтардың арасындағы әсер электр өрісі арқылы жүзеге асырылады. Кез-келген заряд өзінің айналасында кеңістіктің қасиетін өзгертеді - онда электр өрісін туғызады. Берілген жерде өрістің барын анықтау үщін ол жерге зарядталған денені орналастырып, ол электр күштерінің әсерін байқай ма жоқ па соны анықтаймыз. Сөйтіп, электр өрісін біліп, зерттеу үшін белгілі бір “сынақ” зарядты пайдалану керек.
 - бұл векторлық шаманы берілген нүктедегі (яғни сынақ
- бұл векторлық шаманы берілген нүктедегі (яғни сынақ  зарядтың f күштің әсеріне ұшырайтын нүктедегі) электр өрісінің кернеулігі деп атайды. Электр өрісінің кернеулігінің өлшем бірлігі: Ньютон бөлінген Кулон (Н/Кл).
зарядтың f күштің әсеріне ұшырайтын нүктедегі) электр өрісінің кернеулігі деп атайды. Электр өрісінің кернеулігінің өлшем бірлігі: Ньютон бөлінген Кулон (Н/Кл).
Потенциал – скалярлық шама, өрістің берілген нүктесіндегі потенциалдық энергияның сыншы зарядқа қатынасы.Өрістің берілген нүктесіндегі түрліше сынақ зарядтардың 
 т.б. энергиялары түрліше
т.б. энергиялары түрліше  ,
,  т.б. болады. Алайда,
т.б. болады. Алайда, 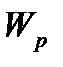 / q
/ q  қатынасы барлық зарядтар үшін бірдей болады:
қатынасы барлық зарядтар үшін бірдей болады: 
Нүктелік заряд өрістің потенциалы: 
Электр өрісінің суперпозиция (беттесу) принципі былай тұжырымдалады: Зарядтар системасының өріс кернеулігі системаның әрбір зарядтары жеке-жеке туғызатын өріс кернеуліктерінің векторлық қосындысына тең: 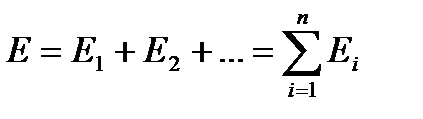
Бұл өрнек электростатикалық өрістің суперпозиция принципі деп аталады. Электрлік диполь деп шамалары жағынан тең, система өрісі анықталатын нүктеге қарағанда ара қашықтығы l едәуір аз әр текті екі, +q және –q нүктелік зарядтан құрылған жүйені айтамыз.
q- 
 q+
q+ 
- + (1-сурет)
Зарядтардың екеуі арқылы өтетін түзу дипольдің осі деп аталады.
Кез келген нүктедегі дипольдің өріс кернеулігі мынадай формула арқылы анықталады:  Мұндағы
Мұндағы  - дипольдің осі мен берілген нүкте бағытының арасындағы бұрыш. Диполь моменті деп - оң зарядтар шамасының зарядтар ара қашықтығына көбейтіндісін және диполь иінінің бағытымен бағыттас векторды айтады:
- дипольдің осі мен берілген нүкте бағытының арасындағы бұрыш. Диполь моменті деп - оң зарядтар шамасының зарядтар ара қашықтығына көбейтіндісін және диполь иінінің бағытымен бағыттас векторды айтады:  Диполь өрісінің кернеулігінің формуласы:
Диполь өрісінің кернеулігінің формуласы:  .
.
32.Вакуумдегі электростатикалық өріс үшін Остраградский-Гаусс теоремасы және оны электр өрісін есептеуге қолдану.
Электр өрісінің  бет арқылы өтетін кернеулік векторының ағыны
бет арқылы өтетін кернеулік векторының ағыны
 , (10.1)
, (10.1)
мұндағы  –
–  векторының
векторының  элементар бетке түсірілген
элементар бетке түсірілген  нормал
нормал
бағытындағы проекциясы.Бұл шама өрістің конфигурациясына ғана емес,  бетке түсірілген
бетке түсірілген  нормаль бағытын таңдауына да байланысты. Тұйықталған бет үшін нормальдың оң бағыты ретінде осы бетпен қамтылған сыртқы аймаққа қарайғы бағыт алынған. Тұйықталған бет арқылы өтетін
нормаль бағытын таңдауына да байланысты. Тұйықталған бет үшін нормальдың оң бағыты ретінде осы бетпен қамтылған сыртқы аймаққа қарайғы бағыт алынған. Тұйықталған бет арқылы өтетін  векторының ағыны осы бет ішіндегі зарядтардың алгебралық қосындысына ғана тәуелді
векторының ағыны осы бет ішіндегі зарядтардың алгебралық қосындысына ғана тәуелді
 . (10.2)
. (10.2)
Бұл формула вакуумдегі электростатикалық өріс үшін Гаусс теоремасын өрнектейді. Гаусс теоремасы былай тұжырымдалады: тұйықталған бет арқылы өтетін  векторының ағыны осы бетпен қамтылған көлем ішіндегі зарядтардың алгебралық қосындысын
векторының ағыны осы бетпен қамтылған көлем ішіндегі зарядтардың алгебралық қосындысын  электр тұрақтысына бөлгенге тең.
электр тұрақтысына бөлгенге тең.
Есепті шығару кезінде  тұйықталған бетті көбінесе Гаусстық бет деп атайды.
тұйықталған бетті көбінесе Гаусстық бет деп атайды.
Симметриялы зарядтар жүйесінің электростатикалық өрісін есептеуде Остроградский-Гаусс теоремасын қолдану ыңғайлы. Ол үшін өріс сипатын анықтап, берілген нүкте арқылы өтетін тұйықталған гаусстық бетті таңдау қажет. Остроградский-Гаусс теоремасын біркелкі зарядталған шексіз сымның, екі параллель шексіз жазықтықтың, зарядталған сфералық және цилиндрлік беттердің электростатикалық өрістерін есептеуге қолдануға болады.
Мысал ретінде  көлемдік зарядпен біркелкі зарядталған, радиусы R дөңгелек цилиндрдің өрісін есептейміз. Гаусстық бет ретінде радиусы r және биіктігі
көлемдік зарядпен біркелкі зарядталған, радиусы R дөңгелек цилиндрдің өрісін есептейміз. Гаусстық бет ретінде радиусы r және биіктігі  болатын, осі берілген цилиндрдің осімен сәйкес келетін дөңгелек цилиндрдің бетін алу ыңғайлы.
болатын, осі берілген цилиндрдің осімен сәйкес келетін дөңгелек цилиндрдің бетін алу ыңғайлы.
 . (10.3)
. (10.3)
Өрістің  аймағы үшін
аймағы үшін  екенін ескеріп алатынымыз
екенін ескеріп алатынымыз
 (10.4)
(10.4)
Ал  жағдай үшін
жағдай үшін
 . (10.4)’
. (10.4)’
Өрістің 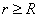 аймағында
аймағында 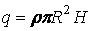 және
және
 . (10.5)
. (10.5)
Өріс потенциалы
 . (10.6.
. (10.6.
33.Электр өрісінде зарядтың орын ауыстыру жұмысы. Потенциал жіне потенциалдар айырмасы. Кернеулік пен потенциалдың арасындағы байланыс. Электр өрісінің циркуляциясы.
Электростатикалық өріс (яғни қозғалмайтын зарядтар туғызатын) күштерінің потенциалдығына тікелей көз жеткізейік. Бұл үшін қозғалмайтын нүктелік q зарядтың өрісіндегі күштердің осы өрістегі  нүктелік зарядтың орын ауыстыруда істеген жұмысын есептейік. Сонда элементар dl жолдағы істелген жұмыс мынаған тең:
нүктелік зарядтың орын ауыстыруда істеген жұмысын есептейік. Сонда элементар dl жолдағы істелген жұмыс мынаған тең:

мұндағы,  . Бұдан 1-2 жолдағы жұмыс үшін мынадай өрнек шығады:
. Бұдан 1-2 жолдағы жұмыс үшін мынадай өрнек шығады:


Осыдан q зарядтың өрісіндегі  зарядтың потенциалдық энергиясы:
зарядтың потенциалдық энергиясы:
 .
.
Өрістің берілген нүктесіндегі түрліше сынақ зарядтардың 
 т.б. энергиялары түрліше
т.б. энергиялары түрліше  ,
,  т.б. болады. Алайда,
т.б. болады. Алайда, 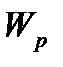 / q
/ q  қатынасы барлық зарядтар үшін бірдей болады:
қатынасы барлық зарядтар үшін бірдей болады: 
Нүктелік заряд өрістің потенциалы: 
Потенциалы  болатын өрістің нүктесіндегі зарядтың потенциалдық энергиясы:
болатын өрістің нүктесіндегі зарядтың потенциалдық энергиясы:

Өріс күштерінің зарядқа істеген жұмысы зарядшамасын бастапқы және ақырғы нүктелердегі потенциалдар айырмасына көбейткенге тең: 
Егер q заряды потенциалы  болып келген нүктеден шексіздікке қашықтатылса (потенциалы нөлге тең жерде), өріс күшінің жұмысы мынаған тең:
болып келген нүктеден шексіздікке қашықтатылса (потенциалы нөлге тең жерде), өріс күшінің жұмысы мынаған тең: 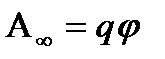 Потенциалдың вольт (В) деп аталатын СИ бірлігі үшін 1 кулонға тең зарядты шексіздіктен осындай нүктеге алып келгенде 1дж жұмыс істеу қажет болатын потенциалы алынады: 1дж=1к*1 В бұдан 1 В =
Потенциалдың вольт (В) деп аталатын СИ бірлігі үшін 1 кулонға тең зарядты шексіздіктен осындай нүктеге алып келгенде 1дж жұмыс істеу қажет болатын потенциалы алынады: 1дж=1к*1 В бұдан 1 В =  .
.
1эв=1.60*10-19к*1в=1.60*10-19дж=1.60*10-12эрг
Потенциал – скалярлық шама, өрістің берілген нүктесіндегі потенциалдық энергияның сыншы зарядқа қатынасы.Өрістің берілген нүктесіндегі түрліше сынақ зарядтардың 
 т.б. энергиялары түрліше
т.б. энергиялары түрліше  ,
,  т.б. болады. Алайда,
т.б. болады. Алайда, 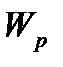 / q
/ q  қатынасы барлық зарядтар үшін бірдей болады:
қатынасы барлық зарядтар үшін бірдей болады:  Нүктелік заряд өрістің потенциалы:
Нүктелік заряд өрістің потенциалы: 
Электр өрісін не векторлық шама Е арқылы, не скаляр шама  арқылы сипаттауға болады. Шынында, өріс күштерінің q
арқылы сипаттауға болады. Шынында, өріс күштерінің q  зарядқа
зарядқа  жол кесіндісіне істеген жұмысы бір жағынан q
жол кесіндісіне істеген жұмысы бір жағынан q  , екінші жағынан зарядтың потенциялық энергиясының кемуі түрінде, яғни -d(q
, екінші жағынан зарядтың потенциялық энергиясының кемуі түрінде, яғни -d(q  ) =- q
) =- q 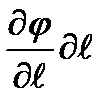 түрінде көрсетілуі мүмкін. Бұл өрнектерді теңестіру ақылы мынаны аламыз:
түрінде көрсетілуі мүмкін. Бұл өрнектерді теңестіру ақылы мынаны аламыз:  .
.
мұндағы  арқылы кеңістікте еркін таңдап алынған бағыт белгіленген. Дербес жағдайда,
арқылы кеңістікте еркін таңдап алынған бағыт белгіленген. Дербес жағдайда,  ,
,  ,
,  .
.
Осыдан: Е=i 
Жақшаның ішіндегі өрнек  скалярдың градиенті (grad
скалярдың градиенті (grad  ) деп аталады.
) деп аталады.
Градиенттің белгілеуін пайдаланып, былай жазуға болады: Е=-grad  .
.
Сөйтіп, электр өрісінің кернеулігі кері таңбамен алынған потенциалдың градиентіне тең.
Кернеулік сызығының ағыны – скалярлы шама. Сонымен, кернеулік ағыны деп – белгілі бір бет арқылы өтетін күш сызықтарының санын айтады. Е сызықтарының жиілігі Е - нің сан мәніне тең болатындай етіп таңдап алынатындықтан, Е векторына перпендикуляр  ауданшаны тесіп өтетін сызықтар саны сан жағынан Е
ауданшаны тесіп өтетін сызықтар саны сан жағынан Е  - ке тең болады. Егер
- ке тең болады. Егер  ауданшасы оған түсірілген нормаль Е векторымен
ауданшасы оған түсірілген нормаль Е векторымен  бұрышын жасайтындай етіп бағдарланған болса, онда ауданшаны тесіп өтетін сызықтар саны сан жағынан мынаған тең болады: Е
бұрышын жасайтындай етіп бағдарланған болса, онда ауданшаны тесіп өтетін сызықтар саны сан жағынан мынаған тең болады: Е 
 . Мұндағы
. Мұндағы  - ауданшаға түсірілген нормаль бойындағы Е вектордың құраушысы.
- ауданшаға түсірілген нормаль бойындағы Е вектордың құраушысы.
Е (кернеулік) вектор ағыны мынаған тең: 
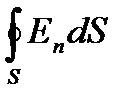 .
.
34. Электростатикалық өрістегі диэлектриктер. Диэлектриктердің түрлері және олардың полярлануы. Байланысқан зарядтар. Поляризация векторы. Поляризация векторы мен кернеулік және байланысқан зарядтардың беттік тығыздығы арасындағы байланыс.
Диэлектриктер - электр өткізбейтін заттар оң зарядтар мен теріс зарядтары тең мөлшерде болып келетін молекулалардан немесе диэлектрик ішінде емін еркін қозғала алмайтын иондардан тұрады.
Сыртқы электр өрісі болмаған кезде оң және теріс зарядтардың ауырлық центрлері бір-біріне қатысты дәл келуі де немесе ығысқан болуы да мүмкін. Соңғы жағдайда молекула электр дипольге эквивалентті болады да полярлық деп аталады. Полярлық молекуланың меншікті электрлік моменті: Р=ql. Өлшем бірлігі:  .
.
Өріс жоқ болғанда әр таңбалы зарядтардың ауырлық центрлері біріккен, меншікті электрлік моменттерге ие болмайтын молекулалар полюссіз деп аталады. Сыртқы электр өрісінің әсерінен полюссіз молекулалардағы зарядтар бір–бірімен салыстырғанда оң зардтар өріс бағытымен, терістері өріске қарсы ығысады. Рационалданған системада пропорционалдық коэффицентті  түрінде жазамыз, мұндағы
түрінде жазамыз, мұндағы  -электрлік тұрақты, ал
-электрлік тұрақты, ал  -молекуланың полюстену қабілеті. p мен E бағыттары дәл келетіндігін ескере отырып былай жазуға болады: Р =
-молекуланың полюстену қабілеті. p мен E бағыттары дәл келетіндігін ескере отырып былай жазуға болады: Р =  .
.
Полюсті емес молекуланың полюстену процесі молекуланың оң және теріс зарядтары өз ара серпімді күштермен байланысқандағыдай болады. Сондықтан полюсті емес молекула сыртқы өрісте өзін серпімді диполь сияқты көрсетеді.
Полюстік молекулаға сыртқы өрістің әсері негізінде молекуланы оның электрлік моменті өріс бағыты бойынша орналасатындай бұруға тырысады. Электрлік моменттің шамасына сыртқы өріс іс жүзінде әсер етпейді. Демек, полюстік молекула сыртқы өрісте өзін қатаң диполь ретінде ұстайды.
Дипольдің моменті мынаған тең:  .
.
Сыртқы өрістің әсерінен диэлектрик поляризацияланады. Мүның өзі диэлектриктің қорытқы электрлік моменті нольден өзгеше болады деген сөз.
Егер өріс немесе диэлектрик біртекті болмаса, диэлектриктің түрліше нүктелеріндегі поляризациялану дәрежесі әр түрлі болады. Берілген нүктедегі
поляризациялануды сипаттау үшін, осы нүктені қамтитын физикалық шексіз кішкентай  көлемді бөліп алу керек. Осы көлемдегі молекулалар моменттерінің қосындысы
көлемді бөліп алу керек. Осы көлемдегі молекулалар моменттерінің қосындысы  тауып, мына қатынасты аламыз:
тауып, мына қатынасты аламыз:  .
. 

Бұл формуламен анықталатын р шамасы диэлектриктің поляризациялану векторы деп аталады. Диэлектриктің кез-келген түрінің поляризациялану векторы сол нүктедегі өріс кернеулігімен қарапайым қатынаспен байланысқан:  .
.
мұндағы  - диэлектрлік өтімділік деп аталатын Е -ге тәуелсіз шама.
- диэлектрлік өтімділік деп аталатын Е -ге тәуелсіз шама.  -өлшемсіз шама.
-өлшемсіз шама.
Диэлектриктер үш топқа бөлінеді: полярлы, полярлы емес және кристалды. Диэлектриктердің бұл үш тобы үйектелудің үш түрімен ерекшеленеді: полярлы емес диэлектриктерде электронды (деформациялы), полярлы диэлектриктерде бағдарланушы (дипольды), ионды кристалдық торлы диэлектриктерде ионды.
Поляризация векторы- векторлық шама, диэлектриктің поляризациялану дәрежесін сипаттайды, бірлік көлемдегі молеккулалар дипольдерінің векторлық қосындылары.
Поляризация салдарынан диэлектрик бетінде компенсацияланбаған зарядтар пайда болады, олар байланысқанзарядтар деп аталады (олардың сыртқы өріс тудыратын еркін зарядтан айырмашылығы).
Байланысқан зарядтар жасайтын диэлектрик ішіндегі өріс  еркін зарядтар жасайтын
еркін зарядтар жасайтын  сыртқы өріске қарсы бағытталған.
сыртқы өріске қарсы бағытталған.
Диэлектрик ішіндегі қорытқы өріс

Біздің жағдайда өрісті беттік тығыздығы  шексіз зарядталған екі жазықтық жасайды.
шексіз зарядталған екі жазықтық жасайды.  , Сондықтан
, Сондықтан  .
.
Қалыңдығы  және қырының ауданы
және қырының ауданы 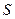 диэлектрлік пластинкаларының толық дипольдік моменті
диэлектрлік пластинкаларының толық дипольдік моменті

екінші жағынан  осыдан
осыдан 
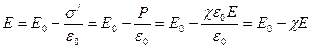 .
.
Осыдан диэлектрик ішіндегі қорытқы өрістің кернеулігі.

Өлшемсіз шама  ортаның диэлектрлік өтімділігідеп аталады.
ортаның диэлектрлік өтімділігідеп аталады.
Бұл диэлектрліктің электрлік өрісте поляризациялану қабілетін және өріс диэлектр арқылы қанша есе нашарлайтындығын көрсетеді.
35.Диэлектриктегі электр өрііс үшін Гаусс теоремасының интегралдық жіне дифференциалдық түрлері. Электрлік ығысу векторы.
Электрлік ығысу (электрлік индукция) өрнегі: 
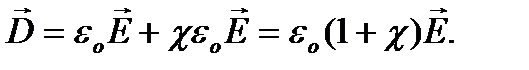
Не нашли, что искали? Воспользуйтесь поиском: