
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
2 страница. Инерциалды санақ жүйесі
Инерциалды санақ жүйесі. Салыстырмалылықтың механикалық принципі және Галилей түрлендірулері. Ньютон механикасындағы жылдамдықтарды қосу заңы.
Денеге сыртқы күштер әсер етпеген жағдайда ол бірқалыпты түзу сызықты қозғалыста болатын санақ жүйелерін инерциалды санақ жүйелері деп атайды.
Галилейдің салыстырмалылық принципі (салыстырмалылықтың механикалық принципі) табиғаттың негізгі қасиеттерін бейнелейді: инерциялық санақ жүйесінің бірқалыпты түзу сызықты қозғалатынын немесе тыныштықта болатынын осы санақ жүйесінде жүргізілетін механикалық тәжірибелер арқылы көрсету мүмкін емес.
Галилейдің салыстырмалылық принципіне Галилейдің түрлендіру координаттары сәйкес келеді. Егер екі инерциалдық санақ жүйелері осьтері бір-біріне параллель және салыстырмалы қозғалыс олардың біреуінде (мысалы, х осінің бойында) (6.1 суретті қара) өтетін болса, Галилей түрлендірулері (тура және кері) мына түрде болады
6.1 Сурет 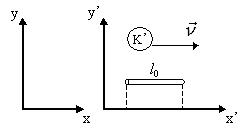
(6.1) 
мұндағы  – К` жүйесінің шартты түрде қозғалмайтын К жүйесіне қатысты жылдамдығы.
– К` жүйесінің шартты түрде қозғалмайтын К жүйесіне қатысты жылдамдығы.
Галилей түрлендіруі кезінде өзгеріссіз қалатын физикалық шамалар Галилей түрлендіруінің инварианттары деп аталады.
Сондай шамалардың бірі - үдеу
 (6.2)
(6.2)
,
үдеу Ньютонның екінші заңының да инвариантты екенін көрсетеді 
Классикалық механиканың негізгі инварианттарының арасында кеңістіктік интервал 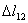 (екі кеңістіктік нүктелердің ара қашықтығы)
(екі кеңістіктік нүктелердің ара қашықтығы)
, (6.3) 
және уақыт интервалы орын алады
(6.4) 
Классикалық механикада инвариантты емес шамаға жылдамдық жатады. Жылдамдықтарды қосудың классикалық заңы бойынша
. (6.5) 
Салыстырмалылық принципі мен Галилей түрлендірулері классикалық механика негізін құрайтын абсолют кеңістік пен абсолют уақыт жайында көріністі бейнелейді.
16. Салыстырмалылықтың арнайы теориясының постулаттары. Бірмезгілділіктің салыстырмалылығы. Лоренц түрлендірулері.
Салыстырмалылықтың арнайы теориясы - кеңістіктің біртекті және изотроптылығын, уақыттың біртектілігін бейнелейтін кеңістік пен уақыт жөнінде физикалық теория.
Эйнштейн құрған салыстырмалылықтың арнайы теориясы негізін екі постулат құрайды: салыстырмалылықтың жалпылама принципі және вакуумдегі жарық жылдамдығының тұрақтылық принципі:
-барлық физикалық құбылыстар инерциалдық санақ жүйелерінде бірдей өтеді;
- вакуумдегі жарық жылдамдығы барлық инерциалдық санақ жүйелерінде бірдей және ол жарық көздері мен қабылдағыштардың жылдамдықтарына тәуелсіз, яғни универсал тұрақты болады. Оның шамасы
 м/с.
м/с.
Эйнштейннің негізгі постулаттарының салдарлары:
- уақыт әртүрлі санақ жүйелерінде әртүрлі өтеді. Оқиғаның қай санақ жүйесіне қатысты екені көрсетілгенде ғана екі оқиғаның арасындағы белгілі уақыт аралығы болады деп айтуға болады. Қандай да бір санақ жүйесінде бір мезгілде өтетін оқиғалар басқа санақ жүйелерінде басқаша өтеді;
- К және К` санақ жүйелеріндегі бір оқиғаның уақыт аралықтарының салыстырмалылығы

Объектімен бірге қозғалған сағат бойынша есептелген уақыт осы объектінің  меншікті уақыты деп аталады.
меншікті уақыты деп аталады.

Қозғалыстағы сағат қозғалмайтын сағатқа қарағанда баяу жүреді. Сағаты тоқтап тұрған жүйеде уақыт жүрісі баяулайды, сағат қозғалысының әсері оның жұмыс істеуіне байланысты емес, ол тек уақыттың салыстырмалылығын көрсетеді. Сонымен, бірегей әлемдік уақыт болмайды. Уақыт, оның жүрісі, бірмезгілділік ұғымдары салыстырмалы.
Кеңістік интервалдарының салыстырмалылығы

Салыстырмалылықтың арнайы теориясында кеңістік пен уақыттың қасиеттерін бейнелеуші координата мен уақытты релятивистік түрлендіру Лоренц түрлендірулері деп аталады. Осы түрлендіруге сәйкес, К` жүйеден К жүйеге өту (6.9) формуласы арқылы, ал К жүйеден К` жүйеге өту (6.10) формуласы арқылы жүзеге асады.
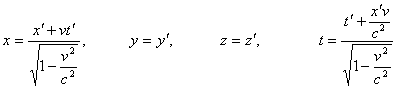 , (6.9)
, (6.9)
 (6.10)
(6.10)
Координата мен уақыт түрлендірулері негізінде салыстырмалылық принципінің тағы бір тұжырымын беруге болады: физикалық заңдар Лоренц түрлендірулеріне қатысты инвариантты болады.
Лоренц түрлендірулерінің кейбір салдарларын қарастырайық. Бірін-шіден, Лоренц түрлендірулері біздің әлемдегі кеңістік пен уақыттың қасиеттерінің бір-бірінен ажырамас байланысы бар екендігін ашып көрсетеді. Сондықтан, кеңістікті немесе уақытты бөлек қарастыруға болмайды, біздің әлем өмір сүретін кеңістік-уақыт жөнінде айтқан дұрыс болады. Басқаша айтсақ, біздің әлем төрт өлшемді.
Екіншіден, Лоренц түрлендірулері негізінде бірмезгілділіктің салыстырмалылығын сипаттауға болады.
Үшіншіден, (6.5) формуласымен берілген жылдамдықтарды қосудың классикалық заңын жарық жылдамдығына жуық жылдамдықпен қозғалған денелер үшін қолдануға болмайды. Х осі бойымен қозғалған бөлшек үшін жылдамдықтарды қосудың релятивтік заңы
 (6.11)
(6.11)
17. Импульстің релятивистік өрнегі. Релятивистік бөлшек үшін қозғалыс заңы. Кинетикалық энергияның релятивистік өрнегі. Тыныштық энергиясы. Толық энергияны импульс арқылы өрнектеу. Масса мен тыныштық энергиясының өзара байланысы.
Қозғалыстағы релятивистік бөлшектердің массасы олардың жылдамдықтарына тәуелді:
 (12)
(12)
Сонымен, әр түрлі инерциалдық санақ жүйесінде бір бөлшектің массасы әр түрлі. Бір инерциалдық санақ жүйесінен екіншіге ауысқанда табиғаттың барлық заңдары инвариантты екенін бекітетін Эйнштейннің салыстырмалы принципінен Лоренц түрлендірулеріне қарасты физикалық заңдардың теңдеулерін инвариантты шарты шығады: 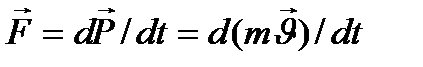 .
.
Динамиканың негізгі теңдеуі Ньютон заңы Лоренцтің түрленуіне қатысты инвариантты болады, егер оның оң жағында релятивистік импульстің уақыт бойынша туындысы тұрса. Материалдық нүктенің релятивистік динамикасының негізгі заңының түрі мынадай болады:  немесе
немесе  (13)
(13)
Мұндағы  (14)
(14)
материалдық нүктенің релятивистік импульсі. Кеңістіктің біртектілігіне байланысты релятивистік механикада релятивистік импульстің сақталу заңы орындалады: тұйық жүйенің релятивистік импульсі сақталады, яғни уақыт өтуіне байланысты өзгермейді.
Релятивистік бөлшектің кинетикалық энергиясын табамыз. Өткен классикалық механикада белгілі элементар орын ауыстырғандағы материалдық нүктенің кинетикалық энергиясының өсімшесі, осы орын ауыстырғандағы күш жұмысына тең
 немесе
немесе  (15)
(15)
мұндағы  ескере отырып және (13) –шы теңдеуді (15) –ке қойып, мына теңдеуді аламыз:
ескере отырып және (13) –шы теңдеуді (15) –ке қойып, мына теңдеуді аламыз:
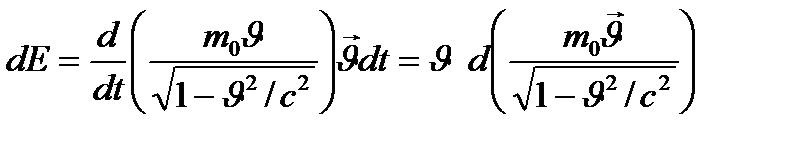 .
.
 екенін ескере отырып, осы теңдеуді және (12) формуланы түрлендіріп, мынадай қорытындыға келеміз:
екенін ескере отырып, осы теңдеуді және (12) формуланы түрлендіріп, мынадай қорытындыға келеміз:
 (16)
(16)
яғни бөлшектің кинетикалық энергиясының өсімшесі оның массасының өсімшесіне пропорционал. Тыныштықта бөлшектің кинетикалық энергиясы нольге тең, ал оның массасы тыныштықтағы  массасына тең, ендеше (16) теңдеуді интегралдап, аламыз
массасына тең, ендеше (16) теңдеуді интегралдап, аламыз
 немесе
немесе  (17)
(17)
осы теңдеу, егер  классикалыққа айналады
классикалыққа айналады  . Эйнштейннің (16) теңдеуін қорыта келіп, бұл тек кинетикалық энергия үшін әділетті емес, сонымен қатар толық энергияға да қатысты. Кез келген массаның өзгеруі
. Эйнштейннің (16) теңдеуін қорыта келіп, бұл тек кинетикалық энергия үшін әділетті емес, сонымен қатар толық энергияға да қатысты. Кез келген массаның өзгеруі  материалдық нүктенің толық энергиясының өзгеруімен сипатталады:
материалдық нүктенің толық энергиясының өзгеруімен сипатталады: 
Осыдан А.Эйнштейн дененің толық энергиясы мен оның массасының арасындағы байланыстың универсиалды екенін көрсетеді:
 (18)
(18)
(17) және (18) теңдеулер табиғаттың фундаментальды заңын көрсетеді - масса мен энергияның арасындағы өзара байланыс заңы: жүйенің толық энергиясы оның массасы мен вакуумдағы жарық жылдамдығының квадрат көбейтіндісіне тең. Толық энергияға сыртқы күш өрісіндегі дененің потенциалдық энергиясы кірмейді. (18) заңды, (17) ескере отырып, былай да жазуға болады:

осыдан, тыныштықтағы дененің энергиясы ( )
) 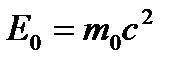 болатын, тыныштық энергиясы деп аталатын энергияға тең болады.
болатын, тыныштық энергиясы деп аталатын энергияға тең болады.
Бұдан  яғни
яғни  энергия мен массаның арасындағы байланыс формуласы шығады.
энергия мен массаның арасындағы байланыс формуласы шығады.
18. Заттардың қасиеттерін статистикалық және термодинамикалық зерттеу әдістері. Молекула-кинетикалық теорияның негізгі қағидалары (МКТ). Идеал газ. Идеал газдың МКТ негізгі теңдеуі. Температура ұғымын молекула-кинетикалық теория тұрғысынан түсіндіру.
МКТ ның негіздері (МКТ) статистикалық тәсілі арқылы газдың физикалық қасиеттерін зерттейтін теория. Молекула кинетикалық теорияның негізі: 1.жүйедегі бөлшектер үшін импульстың, импульс моменттінің, энергиясының, зарядтың сақталу заңдары орындалады және бөлшектер саны тұрақты.2.бөлшектердің бір бірінен айыра аламыз.3.жүйеде өтетін физикалық процестер кеңістік және уақыт бойынша үздіксіз мәндерге ие болады.4.кез келген бөлшек басқа бөлшектерге тәуелсіз координата мен жылдамдық мәндеріне ие болады.
МКТ-нын негізгі теңдеуі газ күйін сипаттайтын параметрлер мен олекулалардың ілгерілемелі кинетикалық энергиясының арасындағы байланыс.
Қандай да бір дененің жылу сыйымдылығы деп оның температурасын бір градусқа көтеру үшін керекті жылу мөлшеріне тең шаманы айтады. Егер де денеге берілген dQ жылу мөлшері оның температурасын dТ шамасына арттыратын болса, анықтама бойынша жылу сыйымдылық  . (8.15) болады. (8.15) шамасының өлшем бірлігі Дж/K. Заттың бірлік массасының жылу сыйымдылығы меншікті жылу сыйымдылық деп аталады. Оны біз с әрпімен белгілейтін боламыз және өлшем бірлігі Дж/К· кг.
. (8.15) болады. (8.15) шамасының өлшем бірлігі Дж/K. Заттың бірлік массасының жылу сыйымдылығы меншікті жылу сыйымдылық деп аталады. Оны біз с әрпімен белгілейтін боламыз және өлшем бірлігі Дж/К· кг.  . (8.16)
. (8.16)
Заттың киломолінің жылу сыйымдылығын с әрпімен белгілейміз. с -нің өлшем бірлігі Дж/К·моль. 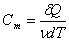 , (8.17) мұндағы
, (8.17) мұндағы  - зат мөлшері.
- зат мөлшері.
Заттың киломолінің жылу сыйымдылығы мен осы заттың меншікті сыйымдылығының арасындағы байланыс: 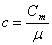 . (8.18)
. (8.18)
Еркіндік дәрежелері бойынша энергияның біркелкі бөліну заңы.Идеал газдың жылулық қозғалысының орташа кинетикалық энергиясы. Идеал газдың ішкі энергиясы.
Еркіндік дәрежесі бойынша энергияның біркелкі таралу заңы - классикалық жүйелерге қолданатын статистиканың негізгі заңдарының бірі. Механикалық жүйенің еркіндік дәрежелері саны деп жүйенің орнын анықтауда мүмкіндік беретін тәуелсіз координаталардың жиынтығын айтады. Материалдық нүктенің кеңістіктегі орны оның үш координаттарының мәндерімен анықталады. Газдардың жылу сыйымдылығын өлшегенде атомдарды материалдық нүктелер деп есептеуге болады. Олай болса, бір атомды молекулалар үш ілгерілемелі еркіндік дәрежеге, екі атомды молекулалар – үш ілгерілемелі, және екі айналмалы, көп атомды молекулалар және абсолютті қатты дене – үш ілгерілемелі және үш айналмалы еркіндік дәрежесіне ие болады. Жылулық тепе-теңдік жағдайында молекуланың әр еркіндік дәрежесіне  тең орташа бірдей кинетикалық энергиядан келеді. Мұндағы,
тең орташа бірдей кинетикалық энергиядан келеді. Мұндағы,  - Больцман тұрақтысы. Екі немесе көп атомды молекулалар айналмалы және тербелмелі қозғалыстар жасайды. Тербелмелі қозғалыстың болуы кинетикалық энергияның потенциалдық энергияға ауысуынан және керісінше болуымен байланысты. Молекуладағы атомның тербеліс энергиясын ескерсек, орташа кинетикалық және орташа потенциалдық энергиясын қарастыруымыз қажет. Молекуланың толық энергиясы
- Больцман тұрақтысы. Екі немесе көп атомды молекулалар айналмалы және тербелмелі қозғалыстар жасайды. Тербелмелі қозғалыстың болуы кинетикалық энергияның потенциалдық энергияға ауысуынан және керісінше болуымен байланысты. Молекуладағы атомның тербеліс энергиясын ескерсек, орташа кинетикалық және орташа потенциалдық энергиясын қарастыруымыз қажет. Молекуланың толық энергиясы 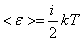 , (8.11) мұндағы i – ілгерілемелі, айналмалы және екі еселенген тербелмелі еркіндік дәрежелері сандарының қосындысы:
, (8.11) мұндағы i – ілгерілемелі, айналмалы және екі еселенген тербелмелі еркіндік дәрежелері сандарының қосындысы:  . (8.12)
. (8.12)
Атомдардың арасында қатаң байланысы бар молекула үшін i молекуланың еркіндік дәрежелерінің санына тең болады.
Массасы m газдың ішкі энергиясы газдың бір молінің энергиясын m массадағы киломольдердің санына көбейткенге тең болады: 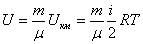 . (8.14)
. (8.14)
Сонымен (8.14) өрнектен берілген газдың массасы үшін ішкі энергия газ молекуласының еркіндік дәреже көрсеткіші өзгермейтін болса, оның абсолют температурасына тура пропорционал екендігі көрінеді.
Идеал газ молекулалары қашықтықтан әрекеттеспейтін болғандықтан, мұндай газдың ішкі энергиясы жеке молекулалардың энергияларының қосындысынан тұрады. Демек, идеал газдың бір киломолінің ішкі энергиясы Авагадро санын бір молекуланың орташа энергиясына көбейткенге тең болады:  . (8.13)
. (8.13)
Массасы m газдың ішкі энергиясы газдың бір молінің энергиясын m массадағы киломольдердің санына көбейткенге тең болады: 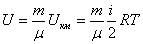 . (8.14)
. (8.14)
Сонымен (8.14) өрнектен берілген газдың массасы үшін ішкі энергия газ молекуласының еркіндік дәреже көрсеткіші өзгермейтін болса, оның абсолют температурасына тура пропорционал екендігі көрінеді.
19.Молекулалардың ең ықтимал, орташа арифметикалық және орташа квадраттық жылдамдықтары. Максвелдің таралу функциясы
Тұрақты температурада тепе-тең күйдегі газ молекулаларының орташа квадраттық жылдамдығы өзгермейді. Бұл молекулалардың жылдамдық бойынша стационарлық таралуының қалыптасатынын білдіреді және Дж. Максвелл шығарған нақты статистикалық заңмен сипатталады.
Максвелл таралуына қолданылатын алғышарттар:
- газ өлшемдері бірдей өте көп молекулалардан құралған;- газ темпера-турасы тұрақты;- газ молекулалары үнемі жылулық қозғалыста болады;
- қозғалыс кеңістіктің барлық бағытында тең ықтималды; - газ молекула-ларына күштік өрістер әсер етпейді.
Молекулалардың жылдамдықтар бойынша таралуы
Жылдамдықтың шексіз аз  интервалына жылдамдықтары
интервалына жылдамдықтары  және
және 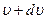 аралығындағы
аралығындағы  молекулалар сәйкес келеді,
молекулалар сәйкес келеді, 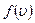 таралу функциясы олардың салыстырмалы санын анықтайды:
таралу функциясы олардың салыстырмалы санын анықтайды: 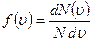 . Яғни, молекулалар жылдамдығының
. Яғни, молекулалар жылдамдығының  және
және 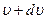 аралығында болу ықтималдығы
аралығында болу ықтималдығы  -ға тең болады.
-ға тең болады.
Дж.Максвелдің идеал газ молекулаларының жылдамдықтар бойынша таралу функциясы газдың табиғатына және температурасына тәуелді:
 . (61)
. (61)
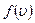 функциясы үшін нормалау шарты: кез келген молекуланың қандай да бір
функциясы үшін нормалау шарты: кез келген молекуланың қандай да бір  жылдамдығы бар, сондықтан жылдамдықтардың мүмкін мәндеріне ие болатын молекулалардың барлық үлесінің қосындысыбірге тең:
жылдамдығы бар, сондықтан жылдамдықтардың мүмкін мәндеріне ие болатын молекулалардың барлық үлесінің қосындысыбірге тең:
 .
.
Молекуланың ең ықтимал жылдамдығы:  , орташа жылдамдығы:
, орташа жылдамдығы:  , орташа квадраттық жылдамдығы:
, орташа квадраттық жылдамдығы:  .
.
Молекулалардың жылулық қозғалыс энергиясы бойынша таралуы
Шамасы  шексіз аз интервалға энергиясы
шексіз аз интервалға энергиясы  және
және 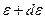 аралығын-дағы
аралығын-дағы  молекулалар саны сәйкес келеді. Молекулалардың жылулық қозғалыс энергиясы бойынша
молекулалар саны сәйкес келеді. Молекулалардың жылулық қозғалыс энергиясы бойынша  таралу функциясы:
таралу функциясы:
 (62)
(62)
Идеал газдың бір молекуласының орташа кинетикалық энергиясы:
 . (63)
. (63)
20. Еркіндік дәрежесі бойынша энергияның біркелкі таралу заңы. Идеал газдың жылулық қозғалысының орташа кинетикалық энергиясы. Идеал газдың ішкі энергиясы.
Молекуланың орташа энергиясы
 (8.10)
(8.10)
молекуланың тек ілгерілемелі қозғалысының энергиясын ғана көрсетеді. Алайда молекулалардың ілгерілемелі қозғалысымен қатар, молекулалардың айналуы және молекуланың қозғалыс құрамына кіретін атомдардың тербелуі де мүмкін. Қозғалыстың бұл екі түрі қандай да бір энергия қорымен байланысты болады, ал бұл энергияны анықтауға статистикалық физика тағайындайтын энергияның молекуланың еркіндік дәрежелері бойынша біркелкі таралуы жөніндегі қағида мүмкіндік береді.
Еркіндік дәрежесі бойынша энергияның біркелкі таралу заңы - классикалық жүйелерге қолданатын статистиканың негізгі заңдарының бірі. Механикалық жүйенің еркіндік дәрежелері саны деп жүйенің орнын анықтауда мүмкіндік беретін тәуелсіз координаталардың жиынтығын айтады. Материалдық нүктенің кеңістіктегі орны оның үш координаттарының мәндерімен анықталады. Газдардың жылу сыйымдылығын өлшегенде атомдарды материалдық нүктелер деп есептеуге болады. Олай болса, бір атомды молекулалар үш ілгерілемелі еркіндік дәрежеге, екі атомды молекулалар – үш ілгерілемелі, және екі айналмалы, көп атомды молекулалар және абсолютті қатты дене – үш ілгерілемелі және үш айналмалы еркіндік дәрежесіне ие болады. Жылулық тепе-теңдік жағдайында молекуланың әр еркіндік дәрежесіне  тең орташа бірдей кинетикалық энергиядан келеді. Мұндағы,
тең орташа бірдей кинетикалық энергиядан келеді. Мұндағы,  - Больцман тұрақтысы. Екі немесе көп атомды молекулалар айналмалы және тербелмелі қозғалыстар жасайды. Тербелмелі қозғалыстың болуы кинетикалық энергияның потенциалдық энергияға ауысуынан және керісінше болуымен байланысты. Молекуладағы атомның тербеліс энергиясын ескерсек, орташа кинетикалық және орташа потенциалдық энергиясын қарастыруымыз қажет. Молекуланың толық энергиясы
- Больцман тұрақтысы. Екі немесе көп атомды молекулалар айналмалы және тербелмелі қозғалыстар жасайды. Тербелмелі қозғалыстың болуы кинетикалық энергияның потенциалдық энергияға ауысуынан және керісінше болуымен байланысты. Молекуладағы атомның тербеліс энергиясын ескерсек, орташа кинетикалық және орташа потенциалдық энергиясын қарастыруымыз қажет. Молекуланың толық энергиясы
 , (8.11)
, (8.11)
мұндағы i – ілгерілемелі, айналмалы және екі еселенген тербелмелі еркіндік дәрежелері сандарының қосындысы:
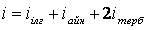 . (8.12)
. (8.12)
Не нашли, что искали? Воспользуйтесь поиском: