Метод опорных векторов

Метод опорных векторов является бинарным классификатором и строит разделяющую функцию в виде

f(x) = w · x + b.

Пусть дана обучающая последовательность (x₁, y₁),...,(x_N, y_N), где x_i — точки пространства признаков, y_i — метки, обозначающие принадлежность одному из классов, принимающие значения 1 или −1. Рассмотрим пока случай линейной разделимости данных. Такое ограничение может быть записано в виде

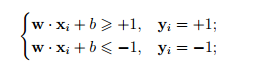
или одним неравенством

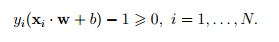
Среди возможных разделяющих гиперплоскостей ищется гиперплоскость, создающая максимальный зазор между классами. То есть расстояние от разделяющей гиперплоскости до ближайших точек каждого класса максимально. 1. Данная задача (так же как описываемые далее обобщения на случай линейной неразделимости и введения нелинейности с помощью функции ядра) может быть решена методами квадратичного про- граммирования. Одним из самых популярных является метод, предложенный в. Для того чтобы обобщить задачу на случай линейной неразделимости, ограничения переписывают в виде

Целевая функция принимает вид

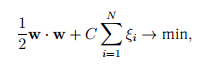
где C — положительная постоянная, задающая степень штрафа за появление ошибок. Другим способом, позволяющим распознавать линейно-неразделимые множества, является введение функции ядра. Идея заключается в том, чтобы отобразить исходное пространство в пространство более высокой размерности, в котором, как может оказаться, множества разделимы. Причём, поскольку всюду в алгоритмах обучения и распознавания признаки используются не отдельно, а в виде скалярных произведений, то нет необходимости в явном виде строить такое преобразование. Достаточно задать функцию ядра, определяющую скалярное произведение в новом пространстве

Среди распространённых можно привести следующие ядра:

— ядро радиальных базисных функций Гаусса, K(x_i, x_j) = (x_i · x_j + 1)ⁿ — полиномиальное ядро. Параметры метода (такие как C и параметры ядра) обычно определяют с помощью перебора некоторого множества значений и оценкой методом кроссвалидации.

Описанные выше методы решают задачу бинарной классификации. Для применения данных методов к задаче многоклассового распознавания используют такие стратегии, как «один-против-остальных» или «один-против-одного». Пусть для обучения получены данные q классов. При использовании стратегии «один-против-остальных» создаются q классификаторов, каждый из которых обучается отличать данный класс от всех остальных. При распознавании объект приписывается к тому классу, чей классификатор выдал наибольшее значение функции f(x). Стратегия «один-против-одного» («каждый против каждого») использует q(q − 1)/2 классификаторов, разделяющих по два класса. Результаты сравнений конкретного класса с каждым из остальных суммируют- ся и затем сравниваются с аналогичными других классов. При этом используют также различные способы преобразования функции f(x) в вероятность P(Ci |x).

Для распознавания последовательности векторов признаков могут быть применены правила, комбинирующие результаты классификации каждого кадра. Используются также подходы, при которых последовательности векторов используются для обучения генеративных моделей, которые затем классифицируются с помощью метода опорных векторов.

Практическая часть

Я проходил преддипломную практику в "Учебном научно-исследовательском центре высокопроизводительных вычислений".

За время прохождения практики были выполнены различные работы, которые поспособствовали написанию моего будущего диплома.
Конкретнее:
>08.02 - 11.02: определился с темой диплома, получил нужную информацию по теме и написанию программного средства;
>12.02 - 15.02: установил "ipp" библиотеку, занимался разбором ее функций;
>16.02 - 19.02: разбор wave - файла;
>20.02 - 23.02: разбор стандартных функций c++ для открытия wav - файла и работы с ним;
>24.02 - 27.02: разбор методов извлечения признаков из wave - файла;
>28.02 - 01.03: разбор методов обработки признаков wave - файла;
>02.03 - 05.03: октрытие и разбор wave - файла в MathCad;
>03.03 - 06.03: извлечения признаков из wave - файла в MathCad;
>07.03 - 08.03: обработка признаков wave - файла в MathCad;
>09.03 - 11.03: тестирование и выбор лучшего метода извлечения признаков из wave - файла для написания на с++;
>12.03 - 14.03: тестирование и выбор лучшего метода обработки wave - файла для написания на с++;
>15.03 - 16.03: обсуждение нюансов с руководителем по написанию программного средства;

>17.03: начал писать программу на с++;
> 18.03: оформление отчета по преддипломной практике.

Не нашли, что искали? Воспользуйтесь поиском: