Представление о стоксовской силе трения, указать условия и границы применимости стоксовской силы. Привести практические примеры действия стоксовской силы трения.

Рассмотрим движение маленького шарика радиуса r в жидкости. Обозначим скорость шарика относительно жидкости через v₀. Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рисунке.

В непосредственной близости к поверхности шарика эта скорость v равна v₀, а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии L от поверхности.

Очевидно, что чем больше радиус шарика, тем большая масса жидкости вовлекается им в движение и, следовательно, L должно быть пропорционально r: L=α·r, где α – коэффициент пропорциональности.

Величина коэффициента пропорциональности α, различна для передней и задней частей движущегося тела.

В связи с этим под α будем понимать среднее значение этого коэффициента.

Тогда среднее значение градиента скорости по поверхности шара равно:

.

Учитывая, что площадь поверхности шара , полная сила трения, испытываемая движущимся шариком, равна: .

Более точное решение уравнений движения вязкой жидкости, проведенное Стоксом, дало для шарика при значении .

Следовательно, сила сопротивления, испытываемая шариком, движущимся в вязкой жидкости, прямо пропорциональна вязкости этой жидкости η, радиусу шарика r и скорости его движения v₀: (*).

Формула (*) носит название закона Стокса. Она применима лишь в случае тел достаточно малых размеров и малых скоростей их движения. При больших скоростях вокруг движущихся тел возникают сложные вихревые движения жидкости. В этом случае сила сопротивления возрастает пропорционально квадрату скорости , а не первой ее степени.

Стоксовская сила трения нашла применение в определении коэффициента вязкости среды.

Задача 5

Определить число молекул, содержащихся в объеме 1 мм³ воды, и массу молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом. Найти диаметр молекул.

Дано:

Решение. Количество вещества равно: ,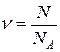

где 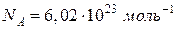- число Авогадро.

Значит, число молекул равно: .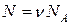

С другой стороны количество вещества равно: .

Значит, , где - молярная масса воды.

Масса воды равна: , где - плотность воды.

Значит, .

Масса молекулы воды равна: .

С другой стороны масса молекулы воды равна: , где - объем капли воды.

Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем: .

Значит, имеем: .

Получаем, , ,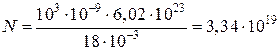

.

Ответ. , , .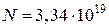

Ответить на теоретические вопросы:

Не нашли, что искали? Воспользуйтесь поиском: