ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сформулировать закон Кулона. Дать определение напряженности электростатического поля.
Закон Кулона – сила взаимодействия между двумя неподвижными точечными зарядами находящимися в вакууме прямо пропорциональна произведению и обратно пропорциональна квадрату расстояния между ними: 
,
где 
– сила взаимодействия между двумя зарядами; Q1 и Q2 – электрические заряды; r – расстояние между зарядами; e – диэлектрическая проницаемость среды; e0 – электрическая постоянная.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля: 
, где 
– напряженность электростатического поля в данной точке; 
– сила, действующая на пробный единичный положительный заряд; Q – единичный положительный заряд.
Задача 10
В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды 2 нКл. Определите напряженность электрического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.
Дано:
|
 
|
Решение. Найдем сначала напряженность в центре квадрата (точка А).
Напряженность, создаваемая точечным зарядом равна: 
,
где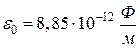 
- электрическая постоянная,
- расстояние от точечного заряда до точки, в которой определяется напряженность.
Тогда,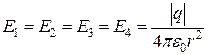 
.
По принципу суперпозиции электростатических полей, суммарная напряженность в точке A равна: 
.
Так как вектора 
и 
компенсируют друг друга (противоположно направлены), а также 
и 
компенсируют друг друга, то суммарная напряженность: 
.
Теперь найдем напряженность в точке, расположенной на середине стороны квадрата (точка В).
По принципу суперпозиции электростатических полей, суммарная напряженность в точке B равна: .
Так как вектора и компенсируют друг друга (противоположно направлены) то имеем: 
.
В проекции на ось х имеем: 
.
Видно, что 
.
Из рисунка видно, что расстояние от заряда 1 (2) равно (по теореме Пифагора):
.
Значит, 
.
Из рисунка видно, что 
.
Тогда, 
.
Проверка размерности: 
.
Получаем, 
.
Ответ. , 
.
Ответить на теоретические вопросы:
Не нашли, что искали? Воспользуйтесь поиском: