Дать определение удельной и молярной теплоемкости газа. Описать уравнение Майера.

Теплоёмкостью тела С называется физическая величина, определяемая в виде отношения

сообщённого телу количества теплоты δQ к вызванному изменению температуры dT:

(*).

Молярной теплоёмкостью называется теплоёмкость одного моля вещества, которая определяет на сколько градусов, например по Кельвину, нагреется один моль вещества при сообщении ему количества теплоты δQ=1 Дж

Удельная теплоёмкость характеризует процесс нагревания или охлаждения единицы массы вещества:

Рассмотрим процесс нагревания идеального газа. Запишем уравнение первого начала термодинамики с учётом уравнения (*), из которого выразим количество тепла

(**).

При постоянстве объёма V=const, dV=0, поэтому (***),

где С_V − теплоемкость газа при постоянном объёме.

Предположим, что для идеального газа теплоёмкость не является функцией температуры, Проинтегрируем уравнение (***): .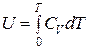

Проинтегрируем далее уравнение (**) при условии постоянства давления p=const:

.

Для реальных газов, молекулы которых расположены друг к другу ближе, чем у идеальных газов, теплоёмкость определяется не только абсолютной температурой, но и объёмом, поэтому

Для идеального газа , т.е. .

При постоянном давлении имеем: .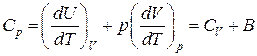

Для идеального газа справедливо уравнение Клапейрона: pdV=BT, которое можно переписать в виде уравнения Майера: .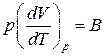

Из полученных уравнений очевидно, что теплоёмкость газа при постоянном давлении больше, чем при постоянном объёме. Дело в том, что при постоянстве давления должен изменяться объём газа, что сопровождается работой против внешних сил, отсюда и неравенство C_p>C_V.

Для одного моля идеального газа уравнение состояния, как известно, записывается в виде , где V_μ − объём одного моля газа,

R − универсальная газовая постоянная.

Значит, .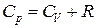

Отношение теплоёмкостей является индивидуальным для каждого газа и зависит от кинетической энергии отдельных молекул.

Величину γ называют коэффициентом Пуассона.

Задача 7

Кислород массой 2 кг занимает объем 1 м³ и находится под давлением 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема 3 м³, а затем при постоянном объеме до давления 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу и теплоту, преданную газу. Построить график процесса.

Дано:

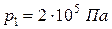
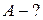
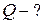
Решение.

Рассмотрим участок 1-2 – изобарный процесс.

Работа в данном случае равна: .

Изменение внутренней энергии равно: ,

где - молярная масса кислорода,

- число степеней свободы кислорода (двухатомный газ).

По уравнению Менделеева-Клапейрона для состояний 1 и 2 имее:

, .

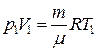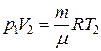Значит, .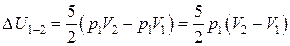

Рассмотрим участок 2-3 – изохорный процесс.

При постоянном объеме работа газа равна нулю: .

Изменение внутренней энергии равно: .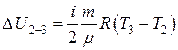

По уравнению Менделеева-Клапейрона для состояний 2 и 3 имеем:

, .

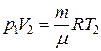Значит, .

Суммарная работа цикла равна: .

Значит, .

Суммарное изменение внутренней энергии равно: .

Значит, .

По первому началу термодинамики имеем: .

Значит, .

Получаем, ,

,

.

Ответ. , , .

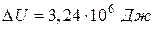Ответить на теоретические вопросы:

Не нашли, что искали? Воспользуйтесь поиском: