Результаты обработки величин амплитуд синусоидальных сигналов

4.3. Исследование импульсного сигнала

1. Соберите схему лабораторной установки согласно рис. 6, и нажмите кнопку на ПИ (ФПЭ-09ПИ).

2. Установите частоту генератора 100 Гц.

3. Получите устойчивую картину прямоугольных импульсов на экране осциллографа. Зарисуйте ее.

4. Измерьте период и длительность прямоугольных импульсов и определите скважность Q по формуле , где Т – период следования импульса, – длительность импульса. Измерения повторите 2-3 раз при различных частотах звукового генератора. Результаты измерений запишите в табл. 4.

Таблица 4

№ п/п	Длительность сигнала	Период сигнала Т	Скважность сигнала Q
В делениях шкалы	Масштаб, с/дел.	В секундах	В делениях шкалы	Масштаб, с/дел.	В секундах

4.4. Исследование фигур Лиссажу

Эта часть работы состоит из 2-х заданий: обязательного (наблюдение фигур Лиссажу – п.4.1) и дополнительного (расчет характеристик). Дополнительное задание выполняется по желанию обучаемого в часы самоподготовки. Его описание изложено в приложении 3.

4.5. Наблюдение фигур Лиссажу

Фигурами Лиссажу называют траектории результирующего движения луча при сложении двух взаимно перпендикулярных колебаний. Эти фигуры можно получить на экране осциллографа, подавая синусоидальные напряжения различной частоты одновременно на горизонтально и вертикально отклоняющие пластины трубки. При этом луч будет находиться под действием двух взаимно перпендикулярных отклоняющих сил. В зависимости от амплитуды, частоты и фазы подаваемых напряжений фигуры Лиссажу будут иметь различный вид (см. главу 18 в [1]).

1. Для наблюдения результатов сложения колебаний в двух взаимно перпендикулярных направлениях (фигур Лиссажу) необходимо собрать установку по схеме рис. 7, а также:

а) подать переменное напряжение 6,3 В от источника питания (ИП) на вход канала А осциллографа;

б) подать напряжение с выхода генератора PQ на вход Б осциллографа;

в) установить переключатель рода работы осциллографа в положение Б, х-у;

г) установить ручку переключателя ВРЕМЯ/ДЕЛ осциллографа в положение x-y.

Наблюдайте сложение взаимно перпендикулярных колебаний одинаковой частоты 50 Гц, но со сдвигом фазы:

– если этот сдвиг является кратным целому числу, то результирующая траектория будет в виде прямой линии;

– если сдвиг фазы равен , где n = 0, 1, 2,..., то фигура будет иметь вид окружности. Промежуточные значения разности фаз дают семейство эллипсов. Медленное превращение фигур Лиссажу одной в другую вызвано нестабильностью начальной фазы колебания в сети переменного тока.

2. Получите и зарисуйте фигуры Лиссажу при соотношении частот 2:1, 1:1, 1:2, 1:3, изменяя частоту звукового генератора. Частота сигнала, подаваемого на осциллограф от источника питания, должна быть равна 50 Гц.

3. Определите соотношение частот сигналов по отношению числа касаний фигуры Лиссажу с прямыми, параллельными осям X и Y.

5. Контрольные вопросы

1. Каково назначение осциллографа?

2. Опишите принцип действия электронно-лучевой трубки.

3. От чего зависит чувствительность трубки осциллографа?

4. Каковы назначения генератора развертки, блока синхронизации, усилителей?

5. Как с помощью осциллографа определяется истинное значение амплитуды измеряемого сигнала?

6. Для чего указаны значения входного сопротивления и емкости осциллографа?

7. Как с помощью осциллографа и генератора определить частоту синусоидального сигнала?

8. Чем определяется погрешность измерения параметров сигналов осциллографом?

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

Вариант 1

1. Курсант дал следующую формулировку закона Кулона: сила взаимодействия двух зарядов пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними. Эта формулировка явно недостаточна. Дайте точную формулировку этого закона, запишите закон Кулона в векторном виде и сделайте соответствующий рисунок.

2. а) Два одинаковых по величине заряда находятся на расстоянии l друг от друга. В каком случае напряжённость поля в точке, лежащей на половине расстояния между ними больше: если эти заряды одноимённые или разноимённые? В каком из случаев потенциал поля в этой точке
больше?

б) В основе метода расчёта электрического поля лежит фундаментальный принцип – принцип суперпозиции. Как на основе этого принципа найти напряжённость поля в произвольной точке, если источником поля является система n точечных зарядов? Как применить этот принцип в том случае, если заряды распределены непрерывно в некоторой области пространства?

в) Используя определение потока вектора через замкнутую поверхность и закон Кулона, докажите, что поток вектора через поверхность сферы, в центре которой находится точечный заряд, равен

3. Электрическое поле создано точечным зарядом. Изобразите эквипотенциальные поверхности и силовые линии поля. Определите работу, совершаемую при перемещении некоторого заряда из точки А в точку В. Сравните работу по перемещению того же заряда на участках АС и ВС.

C А В

4. Предположим, что вблизи небольшого заряженного тела, неподвижного и находящегося в определённом месте, мы перемещаем маленький заряд того же знака. Путём непрерывного перемещения маленького заряда измеряют результирующую силу, действующую на него. Какую линию вычерчивает при этом перемещаемый заряд?

5. Электроскоп – это прибор, который служит для определения наличия электрического заряда на каком-нибудь теле. Металлический стержень с шариком наверху, снабжённый на другом конце двумя очень тонкими металлическими листочками, вставляется через изолирующую пробку в стеклянную банку. К электроскопу поднесли заряженную отрицательно эбонитовую палочку. Какого знака заряды будут на шарике и лепестках? Одинаковы ли потенциалы точек А и В?

А

Вариант 2

1. Имеются два заряженных тела, форма которых, а также расстояние между их центрами показано на рисунке. Можно ли силу взаимодействия между этими заряженными телами вычислить, используя закон Кулона?

2. а) Два одинаковых точечных заряда + Q и – Q находятся на расстоянии l друг от друга. Чему равны потенциал и напряжённость в точках, где находятся заряды? Изобразите качественно график зависимости и вдоль линии, соединяющей заряды (для удобства поместите начало координат в точку, где находится, например, заряд + Q), в трёх указанных областях).

I II III

+Q -Q

б)Известно, что поток вектора напряжённости через произвольную замкнутую поверхность равен Зависит ли этот результат от расположения зарядов внутри объёма, ограниченного данной поверхностью? Представим себе, что алгебраическая сумма зарядов, находящихся в этом объёме равна нулю. Означает ли это, что напряжённость поля в любой точке пространства равна нулю?

Вариант 2

1. Может ли существовать в пустоте электростатическое поле, вектор напряжённости которого во всем объёме поля имеет одинаковое направление, а перпендикулярно к этому направлению изменяется по линейному закону?

2. Проводник находится в поле точечного заряда. Является ли при этом поверхность проводника эквипотенциальной?

3. Для измерения разности потенциалов используется прибор, называемый электрометром. Почему корпус электрометра обязательно должен быть металлическим? Зачем корпус электрометра заземляется?

Вариант 3

1. Имеются две квадратные пластинки со стороной а = 10 см, расположенные параллельно друг другу на расстоянии 5 см. Заряды пластин одинаковые и составляют 10^-7 Кл. Рассчитывая силу взаимодействия между пластинами, курсант использовал закон Кулона. Правильно ли он поступил?

2. а) Два одинаковых точечных заряда Q находятся на некотором расстоянии друг от друга. Чему равны потенциал и напряжённость в точках, где находятся заряды? Изобразите качественно график зависимости и вдоль линии, соединяющей заряды в трёх указанных областях.

I II III

Q Q

б) В каких из указанных случаев напряжённость поля можно вычислить, используя теорему Остроградского-Гаусса:

· имеется равномерно заряженная бесконечно длинная нить;

· имеется конечный отрезок, на котором равномерно распределён заряд;

· имеется сферическая поверхность, заряд на которой распределён равномерно;

· имеется шар, внутри которого существует полость.

Какой из методов вычисления напряжённости поля является более общим: принцип суперпозиции или теорема Остроградского-Гаусса?

3. Сравните работы по перемещению заряда в электрическом поле из точки А и В и из точки А в С и обоснуйте ответ.

В

+Q А

С

4. На рисунке показаны картины силовых линий двух электрических полей:

5.

1 2

а) Какая из этих картинок соответствует однородному полю?

б) Как приблизительно восстановить вид эквипотенциальных поверхностей?

6. Как с помощью датчика, соединённого с электрометром, опытным путем определить вид эквипотенциальной поверхности?

Вариант 4

1. Как известно, закон Кулона установлен экспериментально и справедлив для точечных зарядов. В то же время известно, что точечных зарядов в природе не существует. Для экспериментальной проверки закона Кулона использовались заряженные тела: а) две сферы; б) два кубика и два коротких стержня. В каком случае сила взаимодействия между заряженными телами точно обратно пропорциональна квадрату расстояния между ними?

2. а) Напряженность электрического поля может быть измерена
в единицах В / м или Н / Кл. Покажите, что обе величины эквивалентны.

б)Иногда говорят, что силовые линии электростатического поля – это траектории, по которым двигался бы в поле положительный заряд, если его, внеся в это поле, предоставить самому себе. Правильно ли это утверждение?

в)Могут ли силовые линии электростатического поля пересекаться между собой в той области, где отсутствуют заряды и где напряжённость равна нулю?

г)Заряд q равномерно распределён по тонкому кольцу радиусом R. Чему равен поток вектора напряжённости Е через сферическую поверхность радиуса r<l, центр которой находится в точке А (l – расстояние между точками О и А)?

r

О l А

3. Дана картина расположения эквипотенциальных поверхностей электрического поля (V ₁ >V ₂). а) Каково примерное направление силовых линий этого поля? б) Определите в какой области напряжённость поля больше? в) Заряд перемещается из точки 1 в точку 2. Чему равна работа по перемещению заряда?

1 φ ₂

2 φ ₁

 

4. Имеется бесконечная равномерно заряженная плоскость с поверхностной плотностью s. Рассчитать работу перемещения заряда q по замкнутому прямоугольному контуру.

s

 

5. Пользуясь полученным ответом в п. 4, докажите, что невозможно создать такое электрическое поле, в котором все силовые линии были бы параллельными прямыми, и чтобы их плотность непрерывно увеличивалась в направлении, перпендикулярном к силовым линиям.

 

 

Вариант 5

1. Во сколько раз надо изменить расстояние между точечными зарядами при увеличении одного из них в 4 раза, чтобы сила взаимодействия осталась прежней?

2. а) В двух вершинах равностороннего треугольника со стороной а =0,5 м расположены два одинаковых положительных заряда q ₁ = q ₂ = q = = 10^-6 Кл. Найдите потенциал и напряжённость поля в третьей вершине треугольника. Как изменится результат, если знак одного из зарядов будет отрицательным?

б) Бесконечная плоскость заряжена с постоянной поверхностной плотностью s > 0. Используя теорему Острорадского-Гаусса, найдите напряжённость поля по обе стороны от плоскости. Можно ли этим способом найти напряжённость поля пластинки конечных размеров на расстоянии много большем, чем линейные размеры пластинки? Ответ поясните.

3. Найдите работу, совершаемую силами однородного поля напряжённостью над зарядом q при его перемещении из точки 1 с радиус-вектором в точку 2 с радиус-вектором по произвольной траектории.

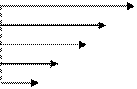
4. Известно, что в электростатическом поле работа при перемещении заряда по любому замкнутому контуру равна нулю. Используя этот факт, докажите, что если на некотором участке силовые линии имеют форму дуг концентрических окружностей с центром в точке О (см. рис.), то напряжённость поля на этом участке должна быть в каждой точке обратно пропорциональна её расстоянию до точки О.

Почему при измерении потенциала проводника его соединяют с электрометром длинной проволокой?

Вариант 6

1. Во сколько раз сила электрического отталкивания между двумя электронами больше силы их гравитационного притяжения друг к другу. Зависит ли это отношение от расстояния между электронами?

2. а) В вершинах квадрата со стороной а находятся одинаковые по величине и по знаку заряды q. Найдите напряжённость и потенциал поля в центре квадрата. Покажите, что на больших расстояниях от квадрата напряжённость поля на прямой, перпендикулярной плоскости квадрата и проходящей через его центр равна

 

 

 

б) Бесконечная пластина шириной а заряжена с постоянной объёмной плотностью r . Найдите напряжённость поля Постройте график зависимости E _x от х.

 

 

 

3. Определите работу сил электрического поля, создаваемого зарядом q ₁ над зарядом q’ при перемещении заряда q’ из точки 1 с радиус-вектором в точку 2 с радиус-вектором по траекториям, изображённым на рис.

 

 

 

 

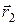
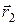
4. Начертите приблизительный вид силовых линий и эквипотенциальных поверхностей изолированного точечного положительного заряда.

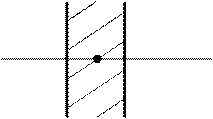
5. Затем на некотором расстоянии от точечного заряда помещают соединенный с землей металлический плоский лист. Изобразите в этом случае вид силовых линий и эквипотенциальных поверхностей.

Вариант 7

1. Два шарика, расположенные на расстоянии 10 см друг от друга, имеют одинаковые отрицательные заряды и взаимодействуют друг
с другом с силой 0,23 мН. Найти число «избыточных» электронов на каждом шарике.

2. а)На кольце радиусом R из изолирующего материала размещены два одинаковых точечных заряда величиной q. Один из них закреплён, а второй может свободно перемещаться по кольцу. Как меняется напряжённость поля в центре кольца, когда второй заряд перемещается по кольцу? Как меняется потенциал поля в центре кольца?

б)На том же кольце равномерно распределён заряд Q. Чему в этом случае равно значение напряжённости поля в центре кольца?

3. Два заряда + q и - q находятся в точках с координатами (a/2, 0, 0) и (-a/2, 0, 0) соответственно. Какую работу совершат силы поля, создаваемого этими зарядами, при удалении заряда q’ из начала координат на бесконечность? Как изменится ответ, если оба заряда одинаковы и равны + q?

4. Потенциал в некоторой области пространства, измеренный экспериментально, определился формулой Какова размерность величины а? Каков её физический смысл? Найдите напряжённость поля.

5. В лабораторной работе перед курсантом стоит задача изучить электростатическое поле прямолинейного бесконечно длинного равномерно заряженного тонкого проводника. В его распоряжении есть электрометр – прибор, позволяющий измерять потенциал в произвольной точке пространства. Предварительно он вычислил потенциал этого поля и получил следующее выражение:

Как он должен перемещать датчик, чтобы получить вид эквипотенциальных поверхностей?

Вариант 8

1. Точечные заряды 40 и –10 нКл расположены на расстоянии 10 см друг от друга в вакууме. Вычислите силу их взаимодействия
(e ₀ = 8,85×10^-12 Ф / м). Изобразите на рисунке силы, действующие на заряды. Чему равны массы этих зарядов, если сила гравитационного взаимодействия между ними равна кулоновской силе (G = 6,67×10^-11 Н × м ²/ кг ²)?

2. а) На кольце радиусом R размещены четыре одинаковых заряда величиной q. Как зависит значение потенциала поля в центре кольца от расположения зарядов на кольце? Как следует закрепить заряды на кольце, чтобы напряжённость поля в центре была бы равна нулю?

б)Заряд q равномерно распределён по тонкому кольцу радиуса R. Центр кольца находится в начале координат, ось х совпадает с осью кольца. Найдите j(x) и E (x) на оси х. Изобразите эти зависимости графически.

3. В центре куба находится заряд q. Чему равен поток вектора :

· через полную поверхность куба;

· через одну из граней куба.

Изменятся ли ответы, если заряд находится не в центре куба, а внутри него?

4. Имеется проводник, форма которого показана на рис. Этому проводнику сообщил отрицательный заряд. Как будет распределён этот заряд на проводнике? Какова будет форма эквипотенциальных поверхностей вблизи поверхности проводника? В какой точке напряжённость поля больше: в точке А или точке В?

А

В

Вариант 9

1. Сила тяготения между двумя наэлектризованными шариками массой по 1 г уравновешена электрической силой отталкивания. Считая заряды шариков равными, определить их величину. Почему при взаимодействии тел малых по массе можно не учитывать гравитационные силы?

2. а) Напряжённость поля где а, b, с – константы. Является ли это поле однородным? Найдите его потенциал , положив = 0.

б) найдите напряжённость поля , если потенциал где с – отрицательная константа, r – расстояние от начала координат до точки наблюдения. Изобразите эквипотенциальные поверхности и силовые линии вектора напряжённости. Является ли это поле однородным?

в)Чему равен поток вектора через поверхность сферы, в центре которой находится: заряд q; диполь с моментом . Объясните результат с помощью картины силовых линий электрического поля. В каком случае для расчёта напряжённости поля можно воспользоваться теоремой Остроградского-Гаусса?

3. Электрическое поле создано бесконечно длинным цилиндром радиуса R =1 см, равномерно заряженным с линейной плотностью
t = 20 нКл / м. Определите работу, совершаемую полем при перемещении заряда q = 10^-7 Кл из точки, находящейся на расстоянии а ₁=0,5 см от поверхности цилиндра в точку, находящуюся от поверхности на расстоянии а ₂ = 2 см. (Указание. Напряжённость поля бесконечно длинного цилиндра равна и направлена перпендикулярно поверхности цилиндра.)

4. Известно, что в трёх «близких» точках 1, 2, 3 потенциалы одинаковы, точки не лежат на одной прямой. Что можно сказать о направлении напряжённости поля в окрестности этих точек?

Вариант 0

1. Двум водяным капелькам радиусом 0,30 мм сообщили одинаковые по величине и знаку электрические заряды. Определите величины зарядов, если сила электрического отталкивания уравновешивается силой взаимного гравитационного притяжения капель.

2.а) Известно, что потенциалы двух близких параллельных эквипотенциальных плоскостей 1 и 2 равны j ₁= 3,00 В, j ₂ = 3,05 В. Расстояние между пластинами l = 0,5 см. Укажите направление и вычислите приближённое значение модуля напряжённости поля Е между этими плоскостями.

б) Имеется бесконечная равномерно заряженная цилиндрическая поверхность. Используя теорему Остроградского-Гаусса, докажите, что внутри цилиндра напряжённость поля равна нулю. Можно ли, используя связь между напряжённостью и потенциалом поля, вычислить значение потенциала внутри цилиндра?

3. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью t = 133 нКл / м. Какую работу А надо совершить, чтобы перенести заряд Q = 6,7 нКл из центра полукольца в бесконечность?

4. Три параллельных металлических пластины А, В и С находятся на расстоянии АВ =1 см; ВС = 2 см друг от друга. Пластины А и С соединены с Землёй. Потенциал пластины В равен 500 В. Найдите напряжённость поля между пластинами А ₁ В и В ₁ С. Изобразите силовые линии поля в областях пространства I, II, III и IV.

 

В

А С

I II III IV

 

Лабораторно-практическая работа

 

⇐ Предыдущая9101112131415161718Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: