
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Порядок выполнения работы. 1. Установите грузы на стержнях на расстоянии, указанном преподавателем
1. Установите грузы на стержнях на расстоянии, указанном преподавателем. Отцентрируйте маятник: установите грузы таким образом, чтобы система находилась в безразличном положении.
2. Измерьте штангенциркулем диаметр шкива пять раз. Найдите радиус R, определите погрешность.
3. Измерьте линейкой путь h, который будет проходить чашечка
с гирями.
4. Намотайте нить на шкив. Поместите на чашечку небольшие грузы для компенсации момента силы трения. Подберите минимальное значение массы грузов, при которой крестовина начнет вращаться. При расчетах масса этого груза не учитывается.
5. Поместите на чашечку груз, имеющий известную массу m. Отпустите груз и одновременно включите секундомер. В момент, когда чашечка коснется пола, остановите секундомер. Время t падения груза определите пять раз. Вычислите среднее значение и погрешность.
6. Рассчитайте по формуле (23) момент инерции и определите погрешность.
7. По указанию преподавателя повторите измерения, наматывая нить на шкив другого диаметра, либо меняя массу груза. Сравните результаты измерений момента инерции и убедитесь, что отношение углового ускорения и момента силы остается постоянным. Результаты измерений занесите в таблицы.
Контрольные вопросы
1. Дайте определения понятиям угла поворота, угловой скорости, углового ускорения, момента силы относительно точки и относительно оси, момента инерции, момента импульса относительно точки и относительно оси.
2. Каков физический смысл момента инерции тела?
3. Как зависит время падения чашечки с гирями от расположения грузов на стержнях крестовины и от диаметра шкива?
4. Можно ли вывести формулу (23), используя закон сохранения энергии?
5. Предложите способ более точного измерения момента инерции и момента силы трения.
Таблица 1
m1 =
| № опыта | d, мм | (d-`d), мм | (d-`d)2, мм2 | t, с | t -`t, с | (t -`t)2, с2 | J, кг×м2 | DJ, кг×м2 |
| Среднее значение, сумма |
Таблица 2
m2 =
| № опыта | d, мм | (d-`d), мм | (d-`d)2, мм2 | t, с | t -`t, с | (t -`t)2, с2 | J, кг×м2 | DJ, кг×м2 |
| Среднее значение, сумма |
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Вариант 1
1. Второй закон Ньютона для материальной точки имеет вид
 (1)
(1)
Дополнительные сведения: 1) определение скорости  2) правило дифференцирования произведения; 3)
2) правило дифференцирования произведения; 3)  Докажите, что если мы умножим обе части уравнения (1) векторным образом на радиус-вектор
Докажите, что если мы умножим обе части уравнения (1) векторным образом на радиус-вектор 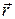 , то получим следующее уравнение:
, то получим следующее уравнение:
2.
 (2)
(2)
Как называются физические величины, входящие в формулу (2)?
3. Почему, говоря о моменте инерции тела необходимо говорить: момент инерции тела относительно оси и указать эту ось? Имеется твердое тело в форме тонкого стержня. Относительно какой из двух указанных осей момент инерции стержня больше?
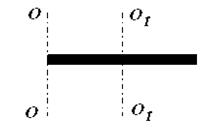
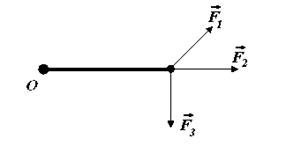
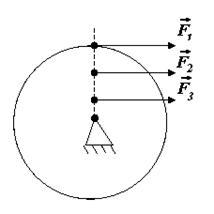
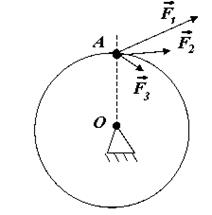
4. В правой части уравнения (2) стоит физическая величина, которая называется моментом силы. Укажите: а) размерность момента силы; б) на край стержня действуют три силы 
 и
и  равные по величине. Момент какой из них будет равен нулю? Момент какой из них будет иметь максимальное значение? Какое направление будут иметь моменты, отличные от нуля? В каком направлении будет вращаться стержень?
равные по величине. Момент какой из них будет равен нулю? Момент какой из них будет иметь максимальное значение? Какое направление будут иметь моменты, отличные от нуля? В каком направлении будет вращаться стержень?
5. Напишите уравнение вращательного движения твердого тела.
6. В лабораторной работе по измерению момента инерции система состоит из блока в виде сплошного цилиндра радиусом 5 см и массой
 = 1 кг. Два грузика массой
= 1 кг. Два грузика массой 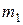 = 100 г и
= 100 г и  = 200 г связаны нитью, перекинутой через блок. Первоначальные грузики находятся на одинаковой высоте от поверхности стола, равной 1 м. Затем их отпускают.
= 200 г связаны нитью, перекинутой через блок. Первоначальные грузики находятся на одинаковой высоте от поверхности стола, равной 1 м. Затем их отпускают.
Тяжелый грузик достигает поверхности стола за 1,3 с. Курсант провел теоретические расчеты и получил, что время падения грузика с этой высоты составляет 0,782 с (при расчетах он брал g = 9,81 м / с 2). Проведя измерения времени падения с разных высот (и теоретические расчеты), он получил следующие данные:
| h, м | t, cизм | t, cтеор |
| 0,1 0,3 0,4 0,9 1,2 | 0,41±0,05 0,71±0,05 0,82±0,05 1,23±0,05 1,43±0,05 | 0,247 0,428 0,495 0,742 0,857 |
Постройте график зависимости квадрата времени падения от высоты. Как по этому графику определить ускорение, с которым движутся грузики?
В чем состоит ошибка, которую допускает курсант при расчетах? Найдя её, определите из экспериментальных данных момент инерции блока, если его радиус равен 5 см.
Вариант 2
1. Второй закон Ньютона для материальной точки имеет вид  (1). Если мы умножим обе части уравнения (1) векторным образом на радиус-вектор
(1). Если мы умножим обе части уравнения (1) векторным образом на радиус-вектор 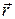 , то после простых преобразований получим следующее уравнение:
, то после простых преобразований получим следующее уравнение:
 (2)
(2)
Используя связь между векторами линейной и угловой скоростями 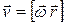 , уравнение (2) можно переписать в следующем виде:
, уравнение (2) можно переписать в следующем виде:
 (3)
(3)
Используя правила вычисления двойного векторного произведения  а также то, что
а также то, что 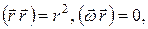 докажите, что уравнение (3) приводится к виду:
докажите, что уравнение (3) приводится к виду:
 (4)
(4)
где  Каков физический смысл величин, входящих в уравнение (4)?
Каков физический смысл величин, входящих в уравнение (4)?
2. В каком направлении будет вращаться система, показанная на рисунке? Массы грузов одинаковы (рис. 1).

 Рис. 1 Рис. 2
Рис. 1 Рис. 2
3. Два одинаковых стержня вращаются с одинаковой частотой вокруг вертикальной оси. Какой стержень обладает большей кинетической энергией и во сколько раз? (Момент инерции стержня относительно оси ОО¢, перпендикулярной стержню, проходящей через центр масс равен 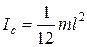 ) (рис. 2).
) (рис. 2).
4. Твердое тело совершает поступательно-вращательное движение. Напишите уравнение движения твердого тела.
5. В лабораторной работе по изучению поступательно-вращательного движения установка имеет вид, показанный на рис. 3.
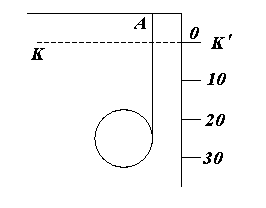
Рис. 3
Блок, имеет форму диска. Его масса M = 1 кг, а радиус равен 10 см. Диск подвешен на нити, накрученной на диск и закрепленной
в точке А. В начальный момент блок накручен на нить и его центр находится на КК¢. Его отпускают без начальной скорости. Результаты измерений курсант занес в таблицу.
| h, м | t, с | h, м | t, с |
| 0,173 | 0,420 | ||
| 0,245 | 0,460 | ||
| 0,300 | 0,490 | ||
| 0,340 | 0,520 | ||
| 0,390 | 0,560 |
а) Каким является это движение?
б) Как по этим данным определить ускорение поступательного движения блока?
в) Момент инерции диска относительно оси вращения равен  Покажите, что экспериментально определенное ускорение и вычисленное совпадают в пределах погрешности.
Покажите, что экспериментально определенное ускорение и вычисленное совпадают в пределах погрешности.
Вариант 3
1. Известно, что уравнение вращательного движения материальной точки относительно неподвижной оси имеет вид
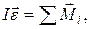 (1)
(1)
где  – момент инерции;
– момент инерции;  – угловое ускорение;
– угловое ускорение;
 – сумма моментов всех сил, действующих на материальную точку.
– сумма моментов всех сил, действующих на материальную точку.
а) Можно ли утверждать, что если 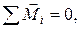 то движение материальной точки всегда будет прямолинейным?
то движение материальной точки всегда будет прямолинейным?
б) Какие физические величины из перечисленных ниже остаются при условии 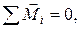 постоянными: 1 – вектор скорости, 2 – вектор угловой скорости; 3 – количество движения; 4 – момент количества движения; 5 – кинетическая энергия точки?
постоянными: 1 – вектор скорости, 2 – вектор угловой скорости; 3 – количество движения; 4 – момент количества движения; 5 – кинетическая энергия точки?
2. В каком направлении будет вращаться блок в системе, показанной на рис.? Зависит ли направление вращения от массы и радиуса блока? (Трением пренебречь.)
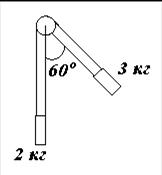
3. Тело имеет форму параллелепипеда. Точка О – его центр масс. Относительно какой оси момент инерции тела будет наибольшим?
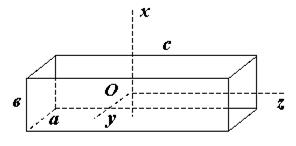
4. На наклонной плоскости находятся шайба, которую можно считать материальной точкой и однородный шар. Изобразите силы, действующие на шайбу и шар. Напишите уравнение движения шайбы и шара. Какую роль играет сила трения в движении шара?
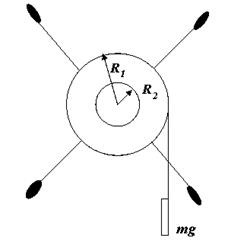
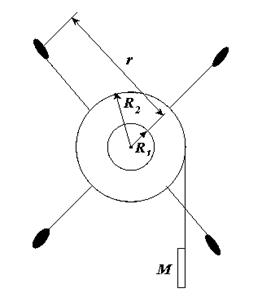
5. В лабораторной работе используется установка (маятник Обербека), показанная на рисунке. В установке предусмотрена возможность менять моменты сил, наматывая на шкивы разных радиусов. Можно ли утверждать, что если намотаем нить на шкив радиуса R 1, а затем на шкив радиуса R 2, то отношение угловых ускорений будет равно  ?
?
Вариант 4
1. Уравнение вращательного движения материальной точки имеет вид: 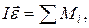 Пусть момент сил, действующих на точку постоянен. Покажите на рис. Направление вращения, направление векторов угловой скорости, углового ускорения и момента сил, если
Пусть момент сил, действующих на точку постоянен. Покажите на рис. Направление вращения, направление векторов угловой скорости, углового ускорения и момента сил, если 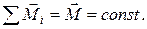 Рассмотрим два случая:
Рассмотрим два случая:  и
и  Какое направление вращения мы принимаем за положительное? Получите зависимость угла поворота от времени.
Какое направление вращения мы принимаем за положительное? Получите зависимость угла поворота от времени.
2. Момент инерции твердого тела относительно некоторой оси находится следующим образом: твердое тело мысленно разбивается на малые объёмы  с массой
с массой 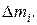 Поскольку твердое тело можно считать суммой элементарных его частей, то и момент инерции тела будет равен сумме моментов инерции элементарных объёмов массами
Поскольку твердое тело можно считать суммой элементарных его частей, то и момент инерции тела будет равен сумме моментов инерции элементарных объёмов массами  относительно заданной оси:
относительно заданной оси:  (
(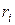 – расстояние от соответствующей массы
– расстояние от соответствующей массы  до оси). Какое дополнительное условие необходимо ввести, чтобы уравнение вращательного движения тела можно было бы записать в следующем виде:
до оси). Какое дополнительное условие необходимо ввести, чтобы уравнение вращательного движения тела можно было бы записать в следующем виде:
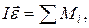
где  – сумма моментов всех сил, действующих на тело относительно заданной оси.
– сумма моментов всех сил, действующих на тело относительно заданной оси.
3. Сплошной цилиндр скатывается с наклонной плоскости. Укажите силы, действующие на цилиндр. Может ли цилиндр скатываться по идеально гладкой наклонной плоскости? Какая разница между скатыванием и скольжением?
4. При движении автомобиля его колеса совершают поступательно-вращательное движение. Какая из указанных точек колеса имеет наибольшую скорость? Мгновенная скорость какой точки равна нулю?
5. В лабораторной работе по определению моментов инерции тел используется устройство, называемое маятником Обербека. Одной из задач является проверка формулы  (I 0 – момент инерции материальной точки, m – масса грузика, r – расстояние от грузика до оси вращения). Рабочая формула для определения момента инерции имеет следующий вид:
(I 0 – момент инерции материальной точки, m – масса грузика, r – расстояние от грузика до оси вращения). Рабочая формула для определения момента инерции имеет следующий вид:

а) Зависит ли результат экспериментального определения момента инерции от радиуса шкива R, на который намотана нить?
б) Зависит ли результат определения момента инерции от массы подвешенного грузика?
Вариант 5
1. Уравнение вращательного движения материальной точки имеет следующий вид:  Дайте определения всех входящих в это уравнение величин.
Дайте определения всех входящих в это уравнение величин.
2. Имеется тело произвольной формы. Выберем точку А на некоторой оси ОO¢. Мысленно разобьем тело на элементарные объёмы с массами  и проведём векторы
и проведём векторы 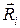 из точки А в точки, где находятся элементарные массы. По какой из приведённых формул можно вычислить момент инерции тела относительно оси ОО¢: а)
из точки А в точки, где находятся элементарные массы. По какой из приведённых формул можно вычислить момент инерции тела относительно оси ОО¢: а) 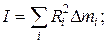 б)
б)  в)
в) 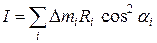 ?
?

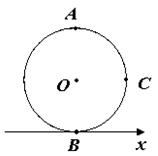
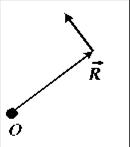
3. Сила  и точка О, относительно которой рассматривается её момент, расположены в пространстве так, как показано на рис. Укажите на рис. плечо силы. Как направлен момент этой силы?
и точка О, относительно которой рассматривается её момент, расположены в пространстве так, как показано на рис. Укажите на рис. плечо силы. Как направлен момент этой силы?
4. Известно, что при движении тел по наклонной плоскости все тела скользят по ней с одинаковым ускорением. Однако опыт показывает, что при скатывании тел это не так. Возьмем шар и сплошной цилиндр. Одинаковой массы и одинакового радиуса. Какой из этих предметов будет двигаться с большим ускорением по наклонной плоскости? (Момент инерции относительно центра масс для шара 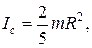 для цилиндра
для цилиндра  ).
).
5. В лабораторной работе по определению моментов инерции тел используется устройство, называемое маятником Обербека. Меняя положение грузиков относительно оси вращения, курсант получил следующую зависимость измеренного момента инерции системы от 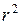
(r –расстояние грузиков от оси вращения). Как по эти данным определить собственный момент инерции установки?

Вариант 6
1. Известно, что если сумма сил, действующих на материальную точку равна нулю, то точка находится в состоянии покоя и прямолинейного равномерного движения. Докажите, что если сумма всех сил равна нулю, то сумма моментов всех сил, действующих на материальную точку относительно любой оси, равна нулю.
2. Теперь заменим материальную точку твердым телом, имеющим конечные размеры. Пусть и в этом случае сумма всех сил, действующих на тело равна нулю. Означает ли это, что и в этом случае сумма моментов сил относительно любой оси равна нулю?
3. Сформулируйте понятие центра масс тела и напишите уравнение поступательного движения твердого тела.
4. С наклонной плоскости без начальной скорости с высоты h скатываются шары радиусом R и массой m и сплошной цилиндр такой же массы и такого же радиуса. Очевидно, что в начальный момент энергии этих тел одинаковы и равны  . Можно ли утверждать, что в любой момент времени механическая энергия этих тел будет одинакова?
. Можно ли утверждать, что в любой момент времени механическая энергия этих тел будет одинакова?
5. В лабораторной работе по определению моментов инерции тел используется устройство, называемое маятником Обербека. Меняя положения грузиков относительно оси вращения, курсант получил следующую зависимость измеренного момента инерции от 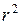 (r – расстояние грузиков от оси вращения).
(r – расстояние грузиков от оси вращения).
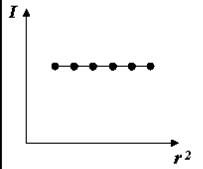
Как можно объяснить эти экспериментальные результаты?
Вариант 7
1. Напишите соотношение между моментом количества движения относительно некоторой оси и моментом внешних сил, действующих на данное тело относительно этой же оси.
2. Можно ли утверждать, что если момент сил, действующих на тело, отличен от нуля и постоянен, то момент количества движения тела сохраняется?
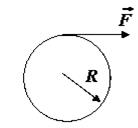
3. Диск радиусом R и массой m может вращаться вокруг неподвижной оси. На диск намотана нить, к концу которой приложена постоянная сила  , в результате чего диск начинает раскручиваться. Найдите кинетическую энергию диска после того, как он совершил один оборот.
, в результате чего диск начинает раскручиваться. Найдите кинетическую энергию диска после того, как он совершил один оборот.
4. Момент инерции шара относительно оси, проходящей через центр масс, равен  Найдите его момент инерции относительно оси, проходящей через точку, расположенную на поверхности шара.
Найдите его момент инерции относительно оси, проходящей через точку, расположенную на поверхности шара.
5. В лабораторной работе по изучению поступательно-враща-тельного движения твердого тела используют шары, сделанные из разных материалов. Для этого шары одинаковой массы, но сделанные из разных материалов отпускают без начальной скорости с наклонной плоскости с высоты h и измеряют время спуска с этой высоты. Будет ли зависеть это время от плотности вещества, из которого изготовлены шарики? Будет ли оно зависеть от радиуса шаров?
Вариант 8
1. Частица массы m движется в положительном направлении вдоль оси х. Найдите момент импульса относительно точек О и О¢. ( ). Укажите направление момента импульса. Координаты точки О¢ (0, -а, 0)
). Укажите направление момента импульса. Координаты точки О¢ (0, -а, 0)
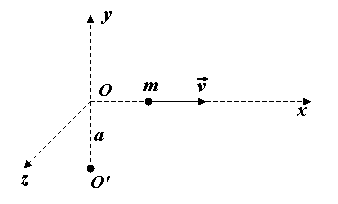
2. Диск насажен на неподвижную ось. К нему прикладывают одну из сил  или
или  (
(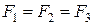 ). Под действием какой из сил диск будет двигаться с большим угловым ускорением?
). Под действием какой из сил диск будет двигаться с большим угловым ускорением?
3. Курсанту дали два цилиндра (одинаково окрашенные) одинакового внешнего диаметра, высоты и массы. Однако известно, что один из них алюминиевый, а другой – свинцовый. Как, наблюдая скатывание цилиндров с наклонной плоскости, различить какой из них алюминиевый, а какой свинцовый?
4. Дайте определение центра масс системы материальных точек.
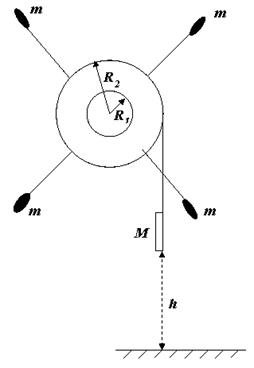
5. В лабораторной работе используется установка (маятник Обер-
бека), показанная на рисунке. Курсант в процессе эксперимента меняет положение грузиков массы m на стержнях. Груз M он поднимает на одну и ту же высоту h и затем отпускает его без начальной скорости.
а) Зависит ли механическая энергия всей системы от положения грузиков?
б) Зависит ли угловое ускорение от положения грузиков?
в) Зависит ли скорость, с которой масса M упадет на стол, от положения грузиков?
Вариант 9
1. Частица массы m движется со скоростью 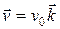 (параллельно оси z) на расстоянии l от оси z. Найдите проекции момента количества движения на оси ОХ; OY и OZ. (
(параллельно оси z) на расстоянии l от оси z. Найдите проекции момента количества движения на оси ОХ; OY и OZ. (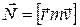 ; векторное произведение вычисляется по формуле).
; векторное произведение вычисляется по формуле).
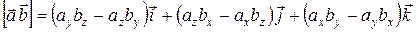
2. Диск насажен на неподвижную ось. К одной и той же точке А диска прикладывают одну из сил  или
или  . Соотношение модулей показано на рис. Под действием какой силы угловое ускорение будет больше?
. Соотношение модулей показано на рис. Под действием какой силы угловое ускорение будет больше?
3. Два стержня одинаковой массы и одинаковой длины вращаются вокруг оси: ось вращения первого стержня проходит через конец стержня, ось вращения другого – через центр масс. Частоты вращения стержней одинаковы. а) Момент инерции стержня относительно оси, проходящей через центр масс равен  Чему равен момент инерции первого стержня? б) Чему равно отношение линейных скоростей концов стержней? в) Чему равно отношение кинетической энергии стержней?
Чему равен момент инерции первого стержня? б) Чему равно отношение линейных скоростей концов стержней? в) Чему равно отношение кинетической энергии стержней?
4. Может ли человек ходить по идеально гладкой горизонтальной поверхности?
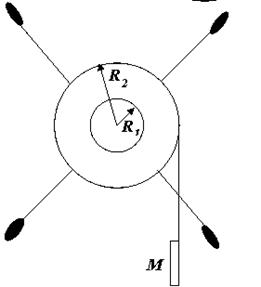
5. В лабораторной работе используется установка (маятник Обер-
бека), показанная на рисунке. В установке предусмотрена возможность изменять момент сил, наматывая нить на шкивы разных радиусов и менять массу груза М. Курсант провел измерения, подвесив массу М, а затем заменил её на массу М 2. Можно ли утверждать, что отношение угловых ускорений будет равно 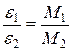 ?
?
Вариант 10
1. Момент импульса материальной точки относительно произвольно выбранной фиксированной точки (например, относительно начала координат) определяется следующим соотношением:
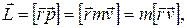
где 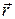 – радиус-вектор, характеризующий положение движущейся точки в выбранной системе координат.
– радиус-вектор, характеризующий положение движущейся точки в выбранной системе координат.
Правило вычисления векторного произведения следующее:
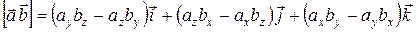
Пусть частица массой m движется равномерно вдоль прямой, уравнение которой  (а и b – постоянные коэффициенты). Покажите, что относительно начала координат
(а и b – постоянные коэффициенты). Покажите, что относительно начала координат  то есть он направлен вдоль оси ОZ.
то есть он направлен вдоль оси ОZ.
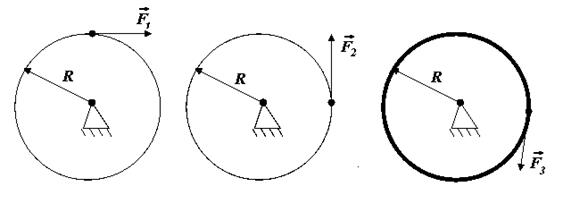
2. Шар, однородной диск и обруч насажены на неподвижные оси. На них действуют силы  или
или  (
(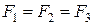 ). Массы тел равны. Какое из тел будет вращаться с наибольшим угловым ускорением?
). Массы тел равны. Какое из тел будет вращаться с наибольшим угловым ускорением?
3. Материальная точка движется по окружности. Её момент количества движения меняется по закону 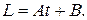 . Как меняется во времени момент сил, действующих на точку?
. Как меняется во времени момент сил, действующих на точку?
4. Колесо находится на идеально гладкой горизонтальной поверхности. К центру колеса приложена горизонтальная сила F. Может ли в этом случае колесо катится по поверхности? Приведите примеры из практики, подтверждающие этот вывод.

5. В лабораторной работе используется установка (маятник Обер-
бека), показанная на рисунке. Одна из задач состоит в экспериментальной проверке формулы для момента инерции материальной точки 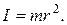 Для этого меняют положение грузиков на стержнях и проводят соответствующие измерения. Рабочая формула для вычисления момента инерции из экспериментальных данных имеет следующий вид:
Для этого меняют положение грузиков на стержнях и проводят соответствующие измерения. Рабочая формула для вычисления момента инерции из экспериментальных данных имеет следующий вид:
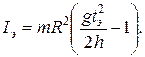
а) Напишите теоретическую формулу для момента инерции уста-
новки.
б) Для сравнения результатов теории и эксперимента обычно строят график зависимости 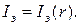 В каких координатах этот график имеет наиболее рациональный вид?
В каких координатах этот график имеет наиболее рациональный вид?
Лабораторно-практическая работа
ЭЛЕКТРОННЫЙ ОСЦИЛЛОГРАФ
1. Цель работы: Ознакомление с устройством и работой электронного осциллографа.
Задачи, решаемые на занятии:
1. Измерение частоты синусоидального сигнала, его амплитудного и действующего значений.
2. Определение скважности прямоугольного импульса.
3. Наблюдение фигур Лиссажу.
2. Краткие теоретические сведения
Электронный (электронно-лучевой) осциллограф принадлежит
к числу приборов, предназначенных для измерения быстро изменяющихся физических величин. К основным элементам осциллографа относят: электронно-лучевую трубку (ЭЛТ), генератор развертки, блок синхронизации, усилители сигналов, подаваемых на отклоняющие пластины, блок цифровых измерений и блок питания (рис. 1).
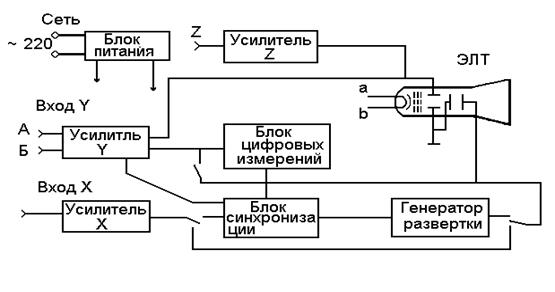
Рис. 1. Схема структурная электронно-лучевого осциллографа
Электронно-лучевая трубка представляет собой стеклянную колбу специальной формы, внутри которой создан высокий вакуум. В ней (рис. 2) последовательно расположены катод, отрицательно заряженный фокусирующий цилиндр, два анода и две пары отклоняющих пластин (конденсаторов). Внутренняя поверхность экрана ЭЛТ покрыта флюоресцирующим составом.
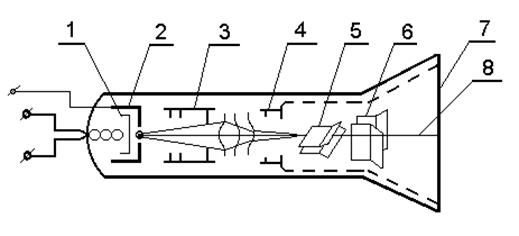
Рис. 2. Электронно-лучевая трубка осциллографа:
1 – катод; 2 – фокусирующий цилиндр; 3 – первый анод; 4 – второй анод; 5 – вертикально отклоняющие пластины; 6 – горизонтально отклоняющие пластины; 7 – экран; 8 – пучок электронов.
Принцип работы ЭЛТ основан на законах электростатики, и в первую очередь, на закономерностях электрического поля в вакууме.
Вся совокупность электрических явлений есть следствие движения и взаимодействия зарядов. Существует два вида электрических зарядов: положительные и отрицательные. Материальным носителем отрицательного заряда служит электрон, положительного – протон. Наименьшую величину называют элементарным зарядом, и она равна 1,6 .10-19 Кл. Любой электрический заряд кратен элементарному заряду.
Электрические заряды взаимодействуют друг с другом, причем одноименные заряды отталкиваются, а разноименные – притягиваются.
Силу взаимодействия двух точечных электрических зарядов определяют по закону Кулона:
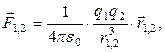 (1)
(1)
где q1 и q2 - величины взаимодействующих зарядов; r1,2 - расстояние между зарядами. Множитель  играет роль коэффициента пропорциональности, который зависит от выбора единиц физических величин, входящих в (1). В системе СИ, где силу выражают в ньютонах, заряд – в кулонах, а расстояние – в метрах,
играет роль коэффициента пропорциональности, который зависит от выбора единиц физических величин, входящих в (1). В системе СИ, где силу выражают в ньютонах, заряд – в кулонах, а расстояние – в метрах,  = 8,85×10 - 12 Ф/ м.
= 8,85×10 - 12 Ф/ м.
При изменении положения заряда q1 будет также происходить изменение величины силы F 1,2 как по модулю, так и по направлению. Обычно говорят, что заряд q 1находится в поле, созданном зарядом q 2. Это поле называют электрическим. Характеристикой его служит вектор, равный силе, действующей на единичный положительный заряд, помещенный в данную точку пространства. Этот вектор называют напряженностью электрического поля E:
 (2)
(2)
Выражение (2) описывает электрическое поле, созданное точечным зарядом q 2 в точке, удаленной на расстояние r 1,2 от него.
Если электрическое поле создано системой точечных зарядов, то для нахождения напряженности результирующего поля используют принцип суперпозиции: напряженность поля системы точечных зарядов равна геометрической сумме напряженностей полей, создаваемых каждым из точечных зарядов в отдельности, независимо от присутствия остальных зарядов:
 (3)
(3)
Зная напряженность электрического поля, можно определить силу, действующую на любой точечный заряд, помещенный в данную точку поля (при условии, что его внесение не изменяет напряженности поля):
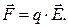 (4)
(4)
Электростатическим называют  поле, созданное неподвижными электрическими зарядами.
поле, созданное неподвижными электрическими зарядами.
Рассмотрим взаимодействие основных элементов ЭЛТ с учетом изложенных закономерностей.
Катод 1 (рис. 2) служит источником электронов (отрицательных зарядов), количество которых регулируется с помощью отрицательно заряженной сетки 2. Вылетев с поверхности катода 1, пучок электронов последовательно проходит первый анод 3, а затем – второй 4. Анод 3, имеющий положительное напряжение несколько сот вольт, фокусирует световой луч в одной точке на экране ЭЛТ. Анод 4 ускоряет движение электронов, т.к. имеет положительный потенциал несколько тысяч вольт.
Пластины 5 и 6 обеспечивают управление электронным пучком, перемещая световое пятно по экрану ЭЛТ.
Электроны (как видно на рис. 2), вылетев с катода 1, проходят через ряд электрических полей, создаваемых зарядами соответствующих элементов. Проходя через них, электроны изменяют траекторию движения, что объясняется силовым взаимодействием движущихся зарядов и полей. Следует заметить, что электростатические поля могут быть однородными, как, например, между парами пластин 5 и 6 (напряженность во всех точках одинаковая), или неоднородными, если напряженность меняется по направлению и величине (между элементами 2, 3, 4 и 5).
Оказалось, что управляющее действие электростатических полей заключено не только в отклонении пучка электронов от первоначального направления. При помощи различных полей можно пучок электронов сделать сходящимся или расходящимся, подобно лучам света.
Этим свойством обладают неоднородные поля, имеющие выпуклые и вогнутые эквипотенциальные поверхности (например, между элементами 2 и 3, 3 и 4, 4 и 5).
Рассмотрим фокусирующее действие электрического поля на примере движения электронов от первого ко второму аноду. Распределение потенциала между ними в пространстве характеризуется эквипотенциальными поверхностями (рис. 3).
Электрическое поле сосредоточено в основном у щели между цилиндрами. Предположим, что электрон влетел в зазор между цилиндрами слева направо под углом к их оси. За время, в течение которого он пролетает зазор между цилиндрами, электрическое поле сообщает ему ускорение вдоль оси (тангенциальные составляющие силы  имеют все время одно направление). В то же время он отклоняется сначала вниз, а потом вверх за счет действия нормальной составляющей
имеют все время одно направление). В то же время он отклоняется сначала вниз, а потом вверх за счет действия нормальной составляющей 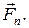
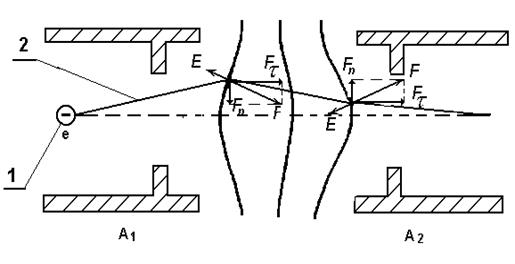
Рис. 3. Схема фокусирующего действия электростатического поля:
E – напряженность; F – сила; A 1, A 2 – первый и второй аноды; 1 – электрон; 2 – траектория электрона; 3 – линии равного потенциала
Следовательно, в электрических полях, эквипотенциальные поверхности которых обращены выпуклостями к катоду, электроны при своем движении будут собираться к горизонтальной оси (действие таких полей похоже на действие собирающих линз). Если эквипотенциальные поверхности полей имеют противоположное направление, то электроны будут расходиться от горизонтальной оси (действие таких полей подобно действию рассеивающих линз).
На пути к экрану электронный пучок проходит между двумя парами отклоняющих пластин. Напряжения, приложенные к пластинам, создают между ними электрические поля, которые отклоняют электронный луч и приводят к смещению светящегося пятна на экране. Горизонтально расположенные пластины отклоняют луч по вертикали (вдоль оси  ),
),
а вертикально расположенные – по горизонтали (вдоль оси 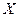 ).
).
Установим связь между напряжением на горизонтальных пластинах А и В и смещением пятна на экране (рис. 4).
Электрон влетает в однородное электрическое поле, имеющее напряженность E у, со скоростью v о = v z. Вдоль оси Z на него не действуют никакие силы, поэтому в этом направлении он движется равномерно:
 (5)
(5)
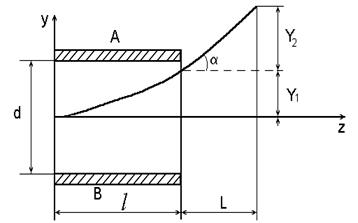
Рис. 4. Схема расчетная смещения электронного пучка горизонтально расположенными пластинами:
А, В – пластины; l -длина пластин; d – расстояние между пластинами; Y, Z – координаты движения электронов; у1,у2, a, L – характеристики траектории электронного пучка
Вдоль оси Y на электрон действует постоянная сила
 (6)
(6)
где Eу – напряженность поля между пластинами:
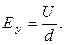 (7)
(7)
Следовательно, движение электрона вдоль оси Y будет равноускоренным:
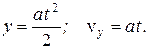
Ускорение a найдем из второго закона Ньютона:
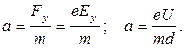
Тогда, учитывая, что  получаем
получаем
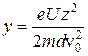 (8)
(8)
Из формулы (8) следует, что траектория движения электрона между пластинами представляет собой параболу. При выходе из пространства между пластинами электрон отклонится от своего первоначального направления на угол  и сместится по оси Y на у1:
и сместится по оси Y на у1:
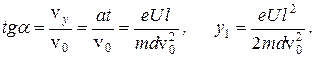
Смещение светящегося пятна на экране равно
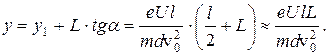
Так как  значительно меньше значения L, то
значительно меньше значения L, то
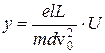
и пропорционально напряжению на отклоняющих пластинах.
Отклонение пятна на экране ЭЛТ (в миллиметрах), вызванное напряжением 1 В на отклоняющих пластинах, называют чувствительностью трубки:
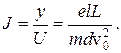
Если Uо - потенциал второго анода относительно катода, то
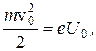 откуда
откуда 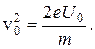
Тогда чувствительность ЭЛТ окажется равной
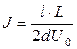
и зависящей, как от расстояния между пластинами и экраном, так и от потенциала на втором аноде.
Для того, чтобы на экране осциллографа можно было увидеть, как в изучаемом физическом процессе некоторая величина y изменяется в зависимости от изменения другой физической величины х, т. е. у = f (х), необходимо на горизонтально отклоняющие пластины подать напряжение Uх, пропорциональное х, а на вертикально отклоняющие пластины одновременно подать напряжение Uу, пропорциональное у.
Тогда электронный луч начертит на экране линию, соответствующую зависимости у = f (х).
Если теперь заставить луч неоднократно повторить тот же путь по экрану, то вследствие инерционности глаза наблюдатель увидит неподвижный график зависимости у = f (х).
|

Рис. 5. Схема сигналов управления движением пучка электронов
по экрану осциллографа:
U – напряжение; t – время; а – изменение напряжения на вертикально отклоняющих пластинах; б – сигнал синхронизации; в – изменение напряжения на горизонтально отклоняющих пластинах; г – результирующий сигнал на экране осциллографа
На практике часто приходится наблюдать изменение физических величин от времени, т. е. у = f (t). В этом случае на вертикально отклоняющие пластины необходимо подать напряжение Uy, пропорциональное исследуемой физической величине у (рис. 5, а), а на горизонтально отклоняющие пластины – напряжение Ux, изменяющееся пропорционально времени t (рис. 5, в).
Для создания напряжения, которое изменяется пропорционально времени, в осциллографе имеется генератор развертки. Под действием вырабатываемого им напряжения луч смещается по экрану ЭЛТ слева направо, причем в любой момент времени это смещение будет пропорционально времени, отсчитываемому от начала движения луча. Одновременно поданное на вертикально отклоняющие пластины напряжение, пропорциональное исследуемой физической величине у, будет смещать луч по вертикали в соответствии с изменением у. Однако, когда луч дойдет до крайнего правого положения, его нужно мгновенно перевести
в исходное положение, а физический процесс повторить сначала. Следовательно, напряжение генератора развертки скачком должно измениться до первоначального значения, а потом снова начать расти по тому же закону. Поэтому зависимость напряжения генератора развертки от времени должна иметь вид, показанный на рис. 5, в. Такое изменение принято называть пилообразным.
Для получения устойчивой картины на экране осциллографа необходимо, чтобы частота пилообразного напряжения совпадала или была меньше в целое число раз частоты повторения изучаемого физического процесса. Поэтому частота напряжения, вырабатываемого генератором развертки, может меняться в широком диапазоне. С по-мощью специального блока синхронизации частота напряжения генератора развертки синхронизируется с исследуемым напряжением любой формы (рис. 5, б), подаваемым на вертикально отклоняющие пластины.
Синхронизация может производиться как напряжением самого исследуемого сигнала, так и напряжением, подаваемым от внешнего источника на специальные гнезда осциллографа. В режиме внутренней синхронизации запуск развертки начинается принудительно с приходом сигнала. В момент времени, когда напряжение сигнала достигает некоторого порога, блок синхронизации вырабатывает короткий импульс
(рис. 5, б). Этот импульс приводит в действие генератор развертки, результатом работы которого является пилообразное напряжение
(рис. 5, в). Это позволяет каждый раз с периодическим приходом сигнала как бы совмещать нуль оси времени. При необходимости сравнения длительности различных процессов, измерениях фазы и т. п. за нуль оси времени можно выбрать момент появления другого сигнала, который и будет запускать генератор в режиме внешней синхронизации. Регулировка порога срабатывания синхронизатора обеспечивается ручкой УРОВЕНЬ (амплитуда синхронизации).
Чувствительность электронно-лучевой трубки, как правило, невелика, поэтому на отклоняющие пластины напряжение подают обычно через усилители. Характеристики усилителей отклоняющих пластин (линейность и диапазон пропускаемых частот) во многом определяют возможности осциллографа.
Порядок настройки и работы конкретной конструкции осциллографа указывается в его техническом описании и инструкции по эксплуатации.
3. Описание методов и установки для экспериментального исследования
Основными методами исследования электрических процессов являются регистрация показателей изучаемых процессов с помощью экрана осциллографа, проведение необходимых расчетов и сравнение полученных результатов с ранее накопленными теоретическими и экспериментальными данными.
Установка экспериментального исследования представляет собой комплект лабораторного оборудования для изучения скоротечных электрических процессов, в который входят осциллограф, звуковой генератор, преобразователь импульсов и источник питания.
В зависимости от задачи исследования это оборудование собирают по одной из схем, представленных на рис. 3.6 и 3.7.
4. Порядок выполнения работы
4.1. Общие положения
1. Изучите конструкцию осциллографа и порядок работы с ним, изложенные в разделе 3.1.2.
2. Соберите схему лабораторной установки в соответствии с выполняемым заданием, используя дополнительный комплект соединительных проводов.
3. Установите ручки управления приборами в начальное положение.
4. Подайте питание 220 В на приборную стойку; контроль за наличием питающего напряжения осуществлять по загоранию контрольных ламп с левой и правой сторон стойки.
5. Включите приборы тумблером СЕТЬ и убедитесь в работоспособности оборудования.
6. Установите на генераторе PQ частоту 50 Гц и выходное напряжение 2,5-3 В, проконтролируйте это значение с помощью цифрового вольтметра. Переключатель генератора < db должен находиться в положении "20". Подача сигнала напряжением более 3 В на кассету ПИ/ФПЭ-09 не допустима.

Рис. 6. Блок- схема для исследования синусоидального и импульсного сигналов
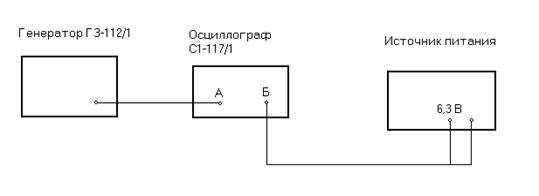
Рис. 7. Блок- схема для наблюдения фигур Лиссажу
4.2. Исследование синусоидального сигнала
1. Соберите схему лабораторной установки согласно рис. 3.6 и нажмите кнопку " ~ " на преобразователе ФПЭ-09 ПИ. Включите приборы и после прогрева установите на генераторе ГЗ-112 частоту 100 Гц. Максимальное выходное напряжение на Г3-112 должно быть не более 3 В. Поставьте переключатель " db " в положение "20", а маленькую ручку поверните вправо до отказа.
2. Получите на экране осциллографа (с помощью ручек V/ДЕЛ, а затем ВРЕМЯ/ДЕЛ – ms/дел, s/дел и Уровень) устойчивое изображение нескольких периодов синусоиды и зарисуйте ее. Во избежание ошибок целесообразно, чтобы масштабы на экране и в тетради были одинаковыми.
3. Измерьте (в делениях сетки экрана электронно-лучевой трубки) величины амплитуды и периода сигнала. Результаты занесите в табл. 3.1. Определите масштабы (коэффициенты отклонения луча осциллографа по вертикали и горизонтали), подсчитайте величины амплитуды (в вольтах) и периода сигнала (в секундах). Результаты измерений запишите
в табл. 1.
4. Повторите, изменяя частоту сигнала звукового генератора, измерения на 4-5 различных частотах. Результаты их также запишите
в табл. 1.
Таблица 1
Не нашли, что искали? Воспользуйтесь поиском: