Результаты измерения и расчета концентрации углекислого газа

№ п.п.	Измеренные значения	Расчетные величины
Количество порций воздуха, поданных грушей 3	Изменение концентрации углекислого газа в сосуде 1
¼	¼	¼	¼	¼
n

Контрольные вопросы

1. Что называется интерференцией волн?

2. Каковы условия максимумов и минимумов при интерференции?

3. Какие волны называются когерентными?

4. От чего зависит расстояние между интерференционными полосами?

5. Назовите области применения интерферометров, аналогичных шахтному?

6. Во сколько раз изменится концентрация примеси в воздухе при двукратном воздухообмене?

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

Вариант 1

1. Можно ли в данном опыте получить интерференционную
картину?

2. Курсант выполняет классический эксперимент Юнга. Для этого он использует: а) экран Е, в котором проделано два маленьких отверстия близко расположенные друг к другу; б) экран Е ¢, параллельный первому; в) точечный источник белого света, который освещает два отверстия.

Курсант отмечает на экране Е ¢ положение f нулевой полосы.

a) После этого он поочередно помещает перед каждым отверстием тонкую плоско параллельную пластинку толщиной h и отмечает новые положения нулевой полосы РP ¢, которые отмечает на экране. Убрав пластинку, он заменяет источник белого света источником монохроматического излучения с длиной волны 0,589 мк, помещая новый источник в ту же точку. Он наблюдает, что на отрезке РP ¢ укладывается 75 интерференционных максимумов.

Как по этим данным определить показатель преломления пластинки, если ее толщина равна 0,05 мм?

б) Затем он измерил длину отрезка РP ¢. Она оказалась равна 5 см, расстояние между экранами Е и Е ¢ равно 1 м. Чему равно расстояние между отверстиями?

3. Ничего не меняя в установке, он помещает всю установку в воду (показатель преломления 4/3). Чему в этом случае будет равно расстояние между интерференционными максимумами?

Вариант 2

1. Можно ли в данном опыте получить интерференционную
картину?

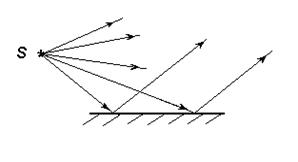
2. Две тонкие параллельные щели F и F¢, использующиеся в эксперименте Юнга, расположены на расстоянии а друг от друга. Они освещаются светом от щели S, которая расположена параллельно F и F¢ на одинаковом расстоянии от них. Длина волны монохроматического излучения от щели S равна l. На экране Р, который расположен параллельно щелям F и F¢ на расстоянии d, наблюдают интерференционную картину. На экране Р измеряют расстояние l, на котором укладываются N интерференционных полос.

a) Выведите формулу, определяющую l как функцию а, d, с и N. Вычислите по этой формуле l, если а = 1,60 мм; d = 80,0 см; l = 3,53 мм;
N = 12.

б) С какой точностью определяется длина волны, если абсолютная погрешность в определении а, d и l соответственно равны 0,01 мм, 0,1 см и 0,02 мм?

3. Затем все устройство опускается в среду с показателем преломления п ₀. Чему равно в этом случае расстояние между интерференционными максимумами?

4. Теперь вся система вновь находится в воздухе. Справа от щели F помещают тонкую плоскопараллельную пластинку с показателем преломления п = 1,510±0,002. При этом центральная полоса сместилась на
х =(4,42±0,01) мм. Объясните это явление и вычислите толщину пластинки и абсолютную погрешность ее определения. (Значения а, D а и d, D d указаны выше.)

Вариант 3

1. Какая из двух интерференционных картин, полученных на одной установке, соответствует облучению красным, а какая синим светом? (Полосы соответствуют максимумам интенсивности.)

2. Две тонкие параллельные щели А и В расположены на расстоянии а = 1 мм друг от друга на экране Е. Они освещаются монохроматическим излучением l = 0,49 мкм от источника S, расположенного на одинаковом расстоянии от щелей.

а) Чему равно расстояние между интерференционными максимумами на экране Е¢, который находится на расстоянии D = 1 м от эк-
рана Е?

б) Затем источник S заменяют другим источником монохроматического излучения неизвестной длины волны. На экране Е¢ наблюдается интерференционная картина и расстояние между интерференционными полосами равно 0,66 мм. Определите длину волны этого излучения.

С какой точностью определяется эта длина волны, если длина участка, на котором располагается 10 интерференционных полос определяется с точностью до 1/20 мм, расстояние а известно с точностью до 0,5 мкм, a расстояние D измерено с точностью до 0,5 мм?

3. Вновь, используя длину волны l = 0,49 мкм, все пространство между Е и Е¢ заполняют прозрачной жидкостью с показателем преломления п. Расстояние между интерференционными максимумами становится равным 0,36 мм. Определите показатель преломления жидкости.

4. Наконец, источник S заменяют источником белого света. Источник находится на расстоянии d от экрана Е. Этот источник перемещают вверх параллельно экрану Е на 3 мм. Докажите, что нулевая полоса на экране Е¢ сместится. Определите направление и величину этого смещения.

5. Затем источник S возвращают в исходное положение. Щель А
с правой стороны закрывают тонкой плоскопараллельной прозрачной пластинкой с показателем преломления 1,55. Докажите, что нулевая полоса при этом переместится. Измерения показали, что это перемещение равно 2,4 мм. Чему равна толщина пластинки?

Вариант 4

1. Какое предположение о природе света необходимо сделать, чтобы объяснить явление интерференции?

2. Собирающая линза с центром С и главной оптической осью ОС дает действительное изображение щели О, перпендикулярной плоскости чертежа. Щель освещается монохроматическим излучением. Линзу разрезают на две равные части и две половинки смещают перпендикулярно главной оптической оси на равные расстояния.

а) Нарисуйте ход световых пучков, исходящих из точки О, которые проходят через каждую половинку линзы.

б) Рассчитайте положение и расстояние между двумя изображениями щели О. Фокусное расстояние линзы F = 20 см, отклонение от оптического центра половинок линз e = 1 мм, расстояние от щели до линзы d = 40 см.

в) На расстоянии 80 см от половинок линз располагают экран
(с той стороны, где формируются действительные изображения щели). Вычислите:

· ширину области экрана, в которой можно наблюдать картину интерференции;

· расстояние между центрами светлых и темных полос;

· число светлых полос на экране;

· число темных полос.

Данные: l = 0,55 мкм, диаметр половинок линз 2 r = 4 см.

4. В место, где формируется изображение щели F верхней полулинзой, помещают маленькую плоскопараллельную стеклянную пластинку толщиной 8 мкм с показателем преломления 1,5. Определите местоположение нулевой полосы в этом случае. Изменится ли расстояние между полосами в этом случае?

Вариант 5

1. Дайте определение монохроматического излучения. Какова структура белого цвета?

2. Светящаяся щель F расположена на расстоянии 40 см от линзы и находится на ее главной оптической оси. Линза обладает оптической силой 5 диоптрий. Она разделена на две половинки сечением, содержащем главную оптическую ось. Эти две половинки слегка раздвинуты в направлении, перпендикулярном главной оптической оси.

а) Покажите, что в этом случае Вы получите два изображения щели F, которые будут параллельны и равны по величине щели F. Будут ли эти изображения когерентными источниками?

б) Расстояние F ₁ F ₂ между этими изображениями равно 1 мм. Чему равно расстояние между половинками линз?

3. На экране Е, перпендикулярном главной оптической оси и расположенном на расстоянии 140 см от линзы, наблюдают картину интерференции. Объясните, как она образуется. Зная, что расстояние между интерференционными полосами равно 0,60 мм, рассчитайте длину волны падающего излучения.

4. Теперь щель F освещают белым светом. Наблюдение курсант проводит за картиной в точке А экрана Е, отстоящей на 4 мм от центральной (нулевой) полосы. Что он видит? Вычислите длины волн из видимого диапазона, для которых интенсивность в этой точке равна нулю. Видимый диапазон лежит в интервале 0,38 мкм £ l £ 0,75 мкм.

Вариант 6

1. Сформулируйте условия, необходимые для наблюдения явления интерференции волн.

2. Бипризма Френеля состоит из двух одинаковых призм с углом преломления 1 град. Показатель преломления материала призмы равен 3/2. Бипризма дает два мнимых изображения тонкой щели F, расположенной на расстоянии 20 см от призмы параллельно ее ребру.

а) Постройте в плоскости чертежа область, в которой можно наблюдать картину интерференции. Чему равна ширина поля интерференции, которое получается на экране, расположенном на расстоянии 6 м отпризмы?

б) Щель F освещается монохроматическим излучением с длиной волны l = 0,56 мкм. Опишите характер возникающей на экране интерференционной картины. Вычислите расстояние между максимумами интерференционной картины.

в) Какой вид будет иметь интерференционная картина, если щель F освещается белым светом?

3. Одну из призм закрывают тонкой плоскопараллельной пластинкой, показатель преломления которой равен 1,696. При этом центральная полоса переместилась на 8,1 мм. Чему равна толщина пластинки?

4. Расстояния между двумя изображениями щели F и их расстояние до экрана известны с точностью 0,01. С какой точностью определяется толщина пластинки?

Вариант 7

1. Можно ли в оптике наблюдать явление интерференции с двумя независимыми источниками, излучающими свет одинаковой частоты?

2. Точечный источник монохроматического излучения – две узкие щели F ₁ и F ₂. Расстояние между щелями 3 мм, а расстояние от источника до каждой из щелей равно 50 см.

На экране Е наблюдают картину интерференции. D = 3 м. Курсант отсчитывает шесть ярких полос с одной и с другой стороны от центральной полосы и измеряет расстояние между крайними полосами а = 7,2 мм.

а) Рассчитать длину волны излучения, испускаемого источником S.

б) Какова точность определения длины волны, если он измерил а
с точностью до 0,1 мм; F ₁, F ₂ с точностью 0,1 мм и D с точностью
до 1 см?

Затем курсант перемещает источник в направлении перпендикулярным главной оптической оси. На сколько и в каком направлении сместится центральная полоса?

Чтобы вернуть центральную полосу в исходное положение, он помещает перед одной из двух щелей плоскопараллельную стеклянную пластинку, показатель преломления которой равен 3/2. Куда он должен ее поместить? Какова толщина пластинки?

Наконец, курсант удаляет экран со щелями F ₁, F ₂ и на его место помещает бипризму Френеля, сделанную из стекла с показателем преломления 3/2. Чему равен преломляющий угол в бипризме, если картина интерференции осталась неизменной?

Вариант 8

1. Как практически получить два когерентных источника?

2. Монохроматический свет длиной волны l = 0,6 мкм от точечного источника освещает щель S и попадает на экран Е, на котором имеются две щели А и В, параллельные S и на одинаковом расстоянии от S. Щель S находится на расстоянии D = 1 м от экрана Е. Расстояние между щелями А и В равно 2 l = 1 мм. На экране Е’, параллельном экрану Е и расположенному на расстоянии 1 м от экрана, наблюдают картину интерференции.

а) Какой вид имеет эта картина?

б) Указать положение центральной полосы (нулевой полосы).

в) На каком расстоянии от центральной полосы наблюдается третья светлая полоса?

Затем перемещают щель S параллельно АВ на расстояние
SS’ = 1 мм. На какое расстояние на экране Е ’ сместится центральная полоса? Теперь возвращают щель S в исходное положение, а щель А закрывают тонкой плоскопараллельной стеклянной пластинкой, толщина которой l = 8 мкм и показатель преломления 3/2. На какое расстояние на экране Е ’ сместится центральная полоса в этом случае?

Вариант 9

1. Имеется плоское зеркало. Постройте изображение точечного источника в этом зеркале. Укажите поле зрения в зеркале. (Поле зрения – это область, в которую следует поместить глаз, чтобы увидеть изображение предмета в зеркале).

2. Для наблюдения явления интерференции курсант использует систему двух плоских зеркал (зеркала Френеля). Эти зеркала М ₁ и М ₂ имеют прямоугольную форму и склеены на одной из сторон О. Угол a очень мал.

Светящаяся очень узкая щель F освещает эти зеркала светом длины волны l ₀.

а) Постройте изображение этой щели в двух зеркалах. Будут ли изображения щели когерентными источниками?

б) Укажите на рисунке область, где световые пучки могут интерферировать. Курсант помещает на расстоянии D от плоскости, в которой лежат изображения, экран Е, параллельный этой плоскости, наблюдает на нем картину интерференции. Какой вид имеет эта картина?

в) Угол a таков, что расстояние между изображениями F ₁ и F ₂ равно а = (1,85±0,01) мм; l ₀ = 0,64 мкм, а расстояние D равно D = (2900±1) мм. Вычислите расстояние между интерференционными максимумами и погрешность определения этого расстояния.

Вариант 10

1. Какой интерференционный максимум называется нулевым? Можно ли отличить нулевой интерференционный максимум от максимума другого порядка (к¹ 0) при использовании монохроматического излучения?

2. В классической установке Юнга для наблюдения интерференции курсант использует два источника S ₁ и S ₂, расположенные на расстоянии
а = 0,4 мм друг от друга.

а) Какую картину интерференции он наблюдает на экране Р, который расположен на расстоянии d = 80 см от плоскости b лежат источники S ₁ и S ₂. Изобразите на рисунке поле интерференции и вычислите полное число интерференционных минимумов, которые наблюдаются в этом поле, если источники излучают свет с длиной волны l = 0,6 мкм.

б) Теперь всю установку помещают в среду с показателем преломления п (п =4/3). Каковы в этом случае размеры поля интерференции в плоскости чертежа на экране Р? Сколько интерференционных минимумов будет наблюдаться на экране Р?

в) Затем курсант раздвигает источники на расстояние 2 мм друг от друга. Изменится ли число интерференционных минимумов в поле интерференции? Если изменится, то на сколько? Зависит ли это изменение от показателя преломления среды, в которой находится установка?

г) Известно, что независимые источники S ₁ и S ₂ не являются когерентными. Как на практике в этом опыте курсант получает два когерентных источника?

Лабораторно-практическая работа

ДИФРАКЦИЯ СВЕТА

1. Цель работы: изучение явления дифракции света и освоение его практического применения.

Задачи, решаемые на занятии:

1. Определение ширины щели.

2. Определение расстояния между центрами двух щелей.

3. Определение периода дифракционной решетки.

Не нашли, что искали? Воспользуйтесь поиском: