РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ

К данной теме относится задача 5.

Кручением называется напряженно-деформированное состояние, при котором из всех силовых факторов в поперечном сечении отличным от нуля является крутящий момент М_х=М_к, являющийся следствием действия касательных напряжений τ

, (3.1)

где ρ=x²+y².

Часто при расчете валов в качестве исходных данных указывается не величина момента, а передаваемая с вала мощность N, кВт. В этом случае величину крутящего момента можно определить по формуле

, (кНм). (3.2)

где ω – угловая скорость вращения вала, рад/с.

, (3.3)

а n – число оборотов в минуту.

Если стержень (вал) имеет круглое или кольцевое поперечное сечение, то он работает в условиях чистого кручения. При этом принимаются следующие допущения:

1. Поперечные сечения, плоские и параллельные до деформации, остаются плоскими и параллельными после деформации, и расстояние между ними не меняется.

2. Поперечные сечения остаются круговыми, радиусы не меняют своей кривизны и не искривляются.

Кроме того, предполагается, что закон Гука остается справедливым и выглядит в форме

, (3.4)

где γ – относительный сдвиг,

G – модуль сдвига.

Исходя из сформулированных выше гипотез, выведена формула для определения касательных напряжений

. (3.5)

Наибольшие напряжения возникаю при ρ=d/2 (d – диаметр сечения)

, (3.6)

где W_p – полярный момент сопротивления (момент сопротивления при кручении),

. (3.7)

Угол закручивания на длине l определяется по формуле

. (3.8)

Довольно часто в рассмотрение вводится относительный угол закручивания

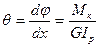, (3.9)

где GI_p – жесткость стержня при кручении.

При расчете на прочность ставится условие:

. (3.10)

При расчете на жесткость –

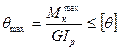. (3.11)

Не нашли, что искали? Воспользуйтесь поиском: