Кореляція.Коефіцієнт кореляції системи випадкових величин

Функціонально пов’язані випадкові величини Х та У можуть набувати різних значень,але якщо Х набуває певного значення,то У відповідає йому.Якщо У залежить не лише від Х,а й від будь-яких інших випадкових чинників,то залежність Х від У не є функціональною.Це стохастична або кореляційна залежність між випадковими величинами,оскільки виявляється вона у зміні розподілу У внаслідок зміни розподілу Х.

Кореляція - залежністю двох випадкових величин. При цьому, зміна однієї або кількох цих величин призводить до систематичної зміни іншої або інших величин. Математичною мірою кореляції двох випадкових величин слугує коефіцієнт кореляції.

Кореляційний аналіз – математичний аналіз зв’язків,що існують між випадковими величинами.

При додатній кореляції групові середні значення однієї ознаки зростають у міру збільшення іншої ознаки;за від’ємної – навпаки.

Для вибірок невеликого обсягу коефіцієнт кореляції визначається за формулою:

Якщо /r/=1,то кореляція між ознаками повна(функціональна),а коли r=0,то зв’язок відсутній.

Регресійний аналіз

Регресі́йний ана́ліз — розділ математичної статистики, присвячений методам аналізу залежності однієї величини від іншої. На відміну від кореляційного аналізу не з'ясовує чи істотний зв'язок, а займається пошуком моделі цього зв'язку, вираженої у функції регресії.Регресійний аналіз полягає в графічному й аналітичному описі кореляційної залежності.

Регресійний аналіз використовується в тому випадку, якщо відношення між змінними можуть бути виражені кількісно у виді деякої комбінації цих змінних. Отримана комбінація використовується для передбачення значення, що може приймати цільова (залежна) змінна, яка обчислюється на заданому наборі значень вхідних (незалежних) змінних. У найпростішому випадку для цього використовуються стандартні статистичні методи, такі як лінійна регресія.
Регресією називається функція, яка дає змогу за величиною однієї ознаки (Х) визначити середні значення іншої (Y) пов язаної з Х кореляційно. Ряд групових середніх (Y або Х) що відображає динаміку мінливості ознаки Х (абоY), називається лінією (графіком) регресії. За графічним записом регресії можна судити про характер кореляційного зв язку між змінними ознаками. На відміну від коефіцієнта кореляції показники регресії – величини іменовані. Таким чином, опис рівнянням регресії дає змогу передбачити можливі зміни однієї ознаки на основі відомих змін іншої, пов язаної з першою кореляційно. У випадку лінійної кореляційної залежності рівняння регресії записується так:

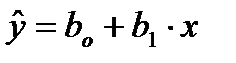
де y – групова середня арифметична. Що відповідає заданому значенню змінної х, b0 і b – параметри рівняння, b0- вільний член, b – показник пропорційності, що називається коефіцієнтом регресії.

Коефіцієнти а і b рівняння лінійної регресії визначають методом найменших квадратів:

Не нашли, что искали? Воспользуйтесь поиском: