Краткие теоретические сведения. При конструировании различных технических устройств, проектировании инженерных сооружений приходится решать задачи о равновесии тел

При конструировании различных технических устройств, проектировании инженерных сооружений приходится решать задачи о равновесии тел, на которые действуют силы, расположенные в одной плоскости. Для решения такого класса задач наряду с умением определять проекции сил на координатные оси, необходимо также научиться находить моменты сил относительно некоторых точек. Поскольку все силы расположены в одной плоскости, можно ограничиться понятием алгебраического момента силы относительно некоторой точки. Здесь же встречается понятие о парах сил.

Произвольной плоской системой сил называют совокупность сил, расположенных в одной плоскости и действующих в различных направлениях.

Алгебраическим моментом силы относительно некоторой точки называют алгебраическую величину, равную произведению модуля силы на плечо силы относительно данной точки, взятую с соответствующим знаком. Обозначение имеет вид .

Плечом силы относительно некоторой точки называют кратчайшее расстояние от этой точки до линии действия силы. Другими словами, это длина перпендикуляра, опущенного из точки на линию действия силы. Знак позволяет сравнивать вращательное действие различных сил по отношению к выбранной точке. Принято ставить знак «плюс», если сила стремиться повернуть тело относительно выбранной точки против хода стрелки часов и знак «минус» – в противном случае.

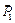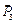Приведем примеры определения алгебраических моментов силы относительно точки (рис. 3.1). Алгебраическими моментами сил , и , приложенных в точках 1, 2 и 3 относительно точки О, будут:

; ; .

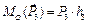Из определения также следует, что, если линия действия силы проходит через заданную точку, то алгебраический момент силы относительно этой точки равен нулю.

Парой сил называют систему двух равных по величине и противоположно направленных сил, не лежащих на одной прямой. Кратчайшее расстояние между линиями действия сил пары называют плечом пары. Из определения следует, что сумма проекций сил пары на любую ось равна нулю. При решении задач на равновесие тел под действием произвольной плоской системы сил удобно пользоваться понятием алгебраического момента пары сил. Алгебраическим моментом пары сил называют величину, равную произведению модуля одной из сил пары на плечо пары, взятую со знаком «плюс», если пара стремится вращать тело против хода стрелки часов, и со знаком «минус» – в противном случае. Выражения для алгебраических моментов пар сил, приведенных на рис. 3.2 имеют вид:

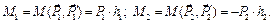
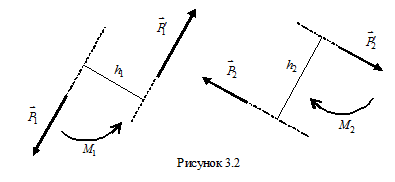
Пары сил, действующие на абсолютно твердое тело, обладают рядом важных свойств:

1) сумма моментов сил, составляющих пару, относительно любой точки в плоскости действия сил равна алгебраическому моменту этой пары сил (не зависит от выбора точки на плоскости);

2) пары сил, лежащие в одной плоскости и имеющие одинаковые алгебраические моменты, эквивалентны, т.е. оказывают на тело одинаковое воздействие. Из этого следует, что пару сил можно переносить в плоскости ее действия в любую область тела, поворачивать как угодно в этой плоскости, менять одновременно модули сил пары и плечо пары так, чтобы величина алгебраического момента пары оставалась неизменной;

3) несколько пар сил, лежащих в одной плоскости, эквивалентны одной паре, алгебраический момент которой равен сумме алгебраических моментов этих пар.

Перечисленные свойства позволяют изображать пары сил дуговыми стрелками, указывающими направление действия, и задавать при этом численные значения их алгебраических моментов (см. рис. 3.2). Согласно основной теореме статики (теореме Пуансо), произвольную систему сил можно заменить эквивалентной системой, состоящей из одной силы, равной главному вектору системы сил, и одной пары, векторный момент которой равен главному моменту системы сил относительно некоторой точки – центра приведения. Напомним, что главным вектором системы сил называют геометрическую сумму сил системы, а главным моментом системы сил относительно некоторой точки – геометрическую сумму моментов сил системы относительно этой точки. Поскольку для системы сил, расположенных в одной плоскости, векторные моменты сил относительно любой точки в этой плоскости являются коллинеарными векторами, то главный момент системы сил равен сумме алгебраических моментов сил относительно этой точки. С другой стороны, главный вектор плоской системы сил лежит в плоскости, в которой расположены силы и, следовательно, имеет только не равные нулю проекции только на оси координат, расположенные в плоскости действия сил. Условия равновесия – равенства нулю главного вектора и главного момента – произвольной плоской системы сил поэтому могут быть записаны в виде:

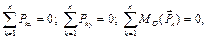(3.1)

где n –количество сил системы; О – центр приведения (в дальнейшем индексы суммирования будем опускать, предполагая, что суммирование производится по всем силам системы); x и y – оси декартовой системы координат, расположенные в плоскости действия сил системы. Условия (3.1) представляют собой аналитические условия равновесия, записанные в первой (основной) форме. Существуют и другие формы условий равновесия, однако при этом накладываются некоторые ограничения на выбор координатных осей или центра приведения. Например, можно использовать и такие условия:

(3.2)

где A и B – любые точки, лежащие в плоскости действия сил, а ось x – ось, не перпендикулярная отрезку ,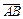

или такие условия:

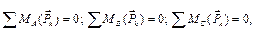(3.3)

где A, B и С – любые точки, не лежащие на одной прямой.

Если в условиях равновесия часть сил неизвестна и из них должна быть найдена, тогда эти условия становятся системой линейных алгебраических уравнений. Разрешимость такой системы изучают в линейной алгебре. Следует отметить, что для получения единственного решения число неизвестных сил должно быть равно числу уравнений, а определитель матрицы левой части системы – не равен нулю. Для получения более простых уравнений, с точки зрения решения системы, в качестве центра приведения целесообразно принимать точку пересечения линий действия наибольшего числа неизвестных сил, а оси координат выбирать так, чтобы бỏльшая часть сил была либо параллельна, либо перпендикулярна этим осям. Естественно, что если в плоской системе сил все силы параллельны, то, выбрав одну из осей, параллельной силам, получим, что сумма проекций всех сил на другую ось, перпендикулярную первой, тождественно равна нулю. Таким образом, из трех уравнений равновесия для плоской системы параллельных сил остаются только два. Если же линии действия сил пересекаются в одной точке, то, выбрав ее в качестве центра приведения, получим, что сумма алгебраических моментов всех сил относительно этой точки тождественно равна нулю и для решения задачи остается система двух уравнений. Запишем систему (3.1) в виде:

для 1-го случая

(2.4)

где ось x перпендикулярна силам;

для 2-го случая

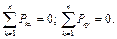(2.5)

Во многих задачах, когда вычисление плеча силы относительно точки затруднено, удобно использовать теорему Вариньона: “Если некоторая система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен сумме моментов всех сил системы относительно той же точки”. Теперь силу можно разложить по линии ее действия на две составляющие и найти сумму моментов этих составляющих относительно выбранной точки. Так, сила , показанная на рис. 3.3, может быть представлена двумя составляющими и , причем 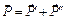, а модули этих составляющих равны, соответственно, 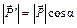и 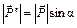. На основании приведенной теоремы момент силы относительно, например, точки О находят по формуле

,

где a и b, соответственно, плечи сил и относительно этой точки.

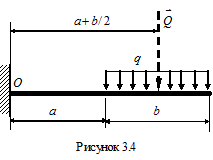Часто встречаются задачи, когда на тело действует нагрузка, равномерно распределенная по какой-либо прямой (рис. 3.4.). Ее задают интенсивностью q, имеющей размерность Н/м и выражающей силу, приходящуюся на единицу длины участка, на котором эта нагрузка действует. Равномерно распределенную нагрузку можно заменить равнодействующей Q, равной произведению интенсивности на длину участка и приложенной посредине этого участка, т.е. 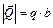. Если, например, необходимо определить значение алгебраического момента равномерно распределенной нагрузки (см. рис. 3.4.) относительно точки O, то используют формулу

.

Для проверки правильности решения задачи записывают дополнительное уравнение, выражающее сумму моментов всех сил относительно любой точки, не использованной при решении задачи. После подстановки в это уравнение найденных значений реакций связей сумма должна быть равной нулю. Наличие погрешностей в вычислениях приводит к тому, что в действительности равенство нулю выполняется неточно. Оценить полученный результат можно с помощью вычисления относительной погрешности, которую определяют, например, по формуле

,

где – модуль полученной суммы; 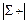– сумма положительных слагаемых. Относительная погрешность зависит от точности вычислений, но не должна превышать 1–3 %. Если погрешность велика, то необходимо проверить правильность записи уравнений равновесия и вычислений при решении.

Не нашли, что искали? Воспользуйтесь поиском: