
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Краткие теоретические сведения. Задачи на равновесие тела, находящегося под действием произвольной пространственной системы сил, представляют собой наиболее общий случай задач о равновесии
Задачи на равновесие тела, находящегося под действием произвольной пространственной системы сил, представляют собой наиболее общий случай задач о равновесии абсолютно твердого тела и имеют важное значение в технике. Новыми элементами при составлении уравнений равновесия является вычисление моментов сил и моментов пар сил относительно координатных осей. При решении данного типа задач необходимо пользоваться понятием вектора-момента пары сил в отличие от алгебраического момента пары.
Моментом силы относительно некоторой оси называют скалярную величину, равную проекции на эту ось вектора-момента силы относительно любой точки на этой оси. Из приведенного определения следует другое правило вычисления указанной величины, часто используемое при непосредственном решении задач. Его формулируют следующим образом: «Момент силы относительно оси равен взятому с соответствующим знаком произведению модуля проекции силы на плоскость, перпендикулярную данной оси, на ее плечо относительно точки пересечения оси с плоскостью». Знак «плюс» ставят тогда, когда поворот тела вокруг данной оси с ее положительного направления наблюдается происходящим против хода стрелки часов, и знак «минус» – в противном случае. Другими словами, момент силы относительно оси равен алгебраическому моменту проекции силы на плоскость, перпендикулярную данной оси, относительно точки пересечения этой плоскости с осью. Из сказанного вытекает, что момент силы относительно оси равен нулю в случаях, если сила параллельна оси (тогда проекция силы на плоскость, перпендикулярную данной оси, равна нулю) или если линия действия силы пересекает ось (тогда плечо равно нулю). Оба указанных случая можно объединить в один – момент силы относительно оси равен нулю, если сила и ось расположены в одной плоскости. Когда,
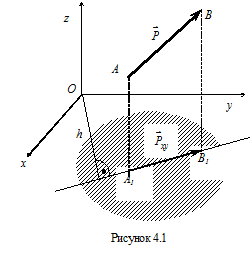
например, оси x, y, z являются тремя взаимно перпендикулярными осями, проведенными из любой точки тела, и нужно определить момент силы  относительно оси z (рис. 4.1), то можно воспользоваться формулой
относительно оси z (рис. 4.1), то можно воспользоваться формулой
 (4.1)
(4.1)
где  – векторная величина, равная проекции силы на плоскость, перпендикулярную оси z, т.е. на плоскость xOy; h – плечо силы
– векторная величина, равная проекции силы на плоскость, перпендикулярную оси z, т.е. на плоскость xOy; h – плечо силы  относительно точки O. Таким образом, необходимо выполнить следующие действия:
относительно точки O. Таким образом, необходимо выполнить следующие действия:
1) определить проекцию силы на плоскость, перпендикулярную данной оси – вектор  ;
;
2) найти точку пересечения данной плоскости с осью (в рассматриваемом примере это точка О);
 в) вычислить алгебраический момент силы
в) вычислить алгебраический момент силы  относительно этой точки, для чего умножить модуль силы на ее плечо относительно точки О, и поставить соответствующий знак. Заметим, что при вычислении алгебраического момента силы относительно точки можно воспользоваться теоремой Вариньона, т.е. разложить удобным образом силу
относительно этой точки, для чего умножить модуль силы на ее плечо относительно точки О, и поставить соответствующий знак. Заметим, что при вычислении алгебраического момента силы относительно точки можно воспользоваться теоремой Вариньона, т.е. разложить удобным образом силу  на две составляющие и определить сумму их моментов относительно точки О.
на две составляющие и определить сумму их моментов относительно точки О.
Если сила  задана проекциями на координатные оси, т.е. величинами Px, Py и P z, а точка приложения силы имеет координаты x, y, z, то для определения моментов силы
задана проекциями на координатные оси, т.е. величинами Px, Py и P z, а точка приложения силы имеет координаты x, y, z, то для определения моментов силы  относительно координатных осей можно воспользоваться следующими аналитическими выражениями:
относительно координатных осей можно воспользоваться следующими аналитическими выражениями:
 (4.2)
(4.2)
Действие пары сил на твердое тело полностью определяется вектором-моментом пары. В теории пар сил доказано, что вектор-момент пары сил – это свободный вектор, не имеющий точки приложения, другими словами, такой вектор может считаться приложенным в любой точке тела. Напомним, что вектор-момент пары сил – это вектор, перпендикулярный плоскости, в которой расположены силы пары, а его модуль равен произведению модуля одной из сил пары на плечо пары. Направлен вектор-момент пары сил так, что вращение тела силами пары наблюдается с его конца происходящим против хода стрелки часов. Две пары сил эквивалентны, если равны их векторы-моменты. Две и более пар сил, действующих на абсолютно твердое тело, можно заменить одной парой, векторный момент которой равен геометрической сумме векторов-моментов этих пар. Если на твердое тело действуют пары сил, то их моменты относительно некоторой оси равны проекциям на данную ось векторов-моментов этих пар.
Для произвольной пространственной системы сил необходимыми и достаточными условиями равновесия является равенство нулю главного вектора и главного момента этой системы сил относительно произвольной точки:
 (4.3)
(4.3)
Аналитические условия равновесия для произвольно выбранной системы декартовых координат имеют вид:

(4.4)

Не нашли, что искали? Воспользуйтесь поиском: