
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения типовых задач. Пример 1. Определить реакции шарнирных опор A и B мостовой фермы (рис
Пример 1. Определить реакции шарнирных опор A и B мостовой фермы (рис. 3.5.), нагруженной равномерно распределенной нагрузкой q = 5 кН/м, сосредоточенной силой P = 20 кН и парами сил с алгебраическими моментами M1 = 30 кН·м, M2 = 15 кН·м, если a = 2 м; b = 3 м; α = 600.

Решение
1) В качестве объекта равновесия примем всю ферму, которую будем считать абсолютно твердым телом.
2) Активными силами, действующими на объект равновесия, будут силы  ,
, 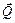 и пары сил с алгебраическими моментами M1, M2. Сила
и пары сил с алгебраическими моментами M1, M2. Сила 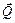 является равнодействующей равномерно распределенной нагрузки q, модуль которой
является равнодействующей равномерно распределенной нагрузки q, модуль которой  кН. Приложена она в середине отрезка длиной a. Силу
кН. Приложена она в середине отрезка длиной a. Силу  целесообразно разложить на составляющие
целесообразно разложить на составляющие 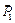 и
и  , параллельные координатным осям
, параллельные координатным осям
 ,
,
модули которых
 кН;
кН;
 кН.
кН.
3) Отбрасывая связи (неподвижный цилиндрический шарнир A и подвижный цилиндрический шарнир B), заменим их действие на объект равновесия реакциями  и
и 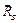 . Реакция неподвижного шарнира
. Реакция неподвижного шарнира  представлена составляющими
представлена составляющими 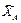 и
и 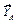 , параллельными координатным осям.
, параллельными координатным осям.
4) Запишем уравнения равновесия (3.1) полученной плоской системы сил в принятой системе координат (см. рис. 3.5). Составим табл. 3.1. Суммируя элементы соответствующих строк таблицы, и приравнивая эти суммы нулю, получим систему уравнений равновесия:



Таблица 3.1
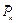
| 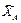
| 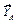
| 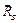
| 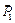
| 
| 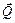
| 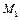
| 
|
| Pkx | 
| 
| – | – | ||||
| Pky | 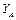
| 
| 
| 
| – | – | ||
MA (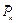 ) )
| 
| 
| 
| 
| 
| 
|
5) Решим полученную систему уравнений, из которых следует:
из 1-го
 кН;
кН;
из 3-го

 кН;
кН;
из 2-го
 кН.
кН.
Знаки «минус» у всех реакций указывают на то, что эти реакции в действительности направлены в стороны, противоположные принятым в соответствии с рис. 3.5.
По составляющим реакции в шарнире А можно определить модуль и направление реакции 
 кН,
кН,

где β – угол, между вектором реакции  и положительным направлением оси x.
и положительным направлением оси x.
Для проверки полученного решения составим выражение суммы моментов всех сил, например, относительно точки D

Вычислим относительную погрешность
 ,
,
которая не превышает 1 % и связана с точностью вычислений.
Пример 2. Определить реакции жесткой заделки А в ломаном брусе (рис. 3.6.), нагруженном распределенными нагрузками интенсивности которых составляют, соответственно, q1 = 2 кН/м и q2 = 5 кН/м, силой P = 30 кН, и моментом M = 8 кН·м, если a = 2 м, b = 3 м, c = 1 м, d = 2 м, α = 300.

Решение
1) В качестве объекта равновесия примем брус AB.
2) Активными силами, действующими на объект равновесия, будут  ,
,  ,
,  и пара сил, алгебраический момент которой M. Силы
и пара сил, алгебраический момент которой M. Силы  и
и  являются равнодействующими распределенных нагрузок
являются равнодействующими распределенных нагрузок  и
и  . Их модули:
. Их модули:  кН;
кН;  кН. Приложены они в середине отрезков длиной b и d (см. рис. 3.6.). Силу
кН. Приложены они в середине отрезков длиной b и d (см. рис. 3.6.). Силу  целесообразно разложить на составляющие
целесообразно разложить на составляющие 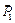 и
и  , параллельные координатным осям,
, параллельные координатным осям,
 .
.
Модули этих составляющих:
 кН;
кН;  .
.
3) Отбрасывая связь (плоскую жесткую заделку A), заменим ее действие на объект равновесия реакцией  , которая представлена составляющими
, которая представлена составляющими 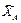 и
и 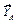 , параллельными координатным осям, и парой сил с алгебраическим моментом MА.
, параллельными координатным осям, и парой сил с алгебраическим моментом MА.
4) Запишем уравнения равновесия (3.1) полученной плоской системы сил в принятой системе координат (см. рис. 3.6), составив предварительно табл. 3.2.
Таблица 3.2
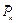
| 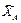
| 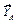
| 
| 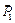
| 
| 
| 
| 
|
| Pkx | 
| – | 
| 
| – | |||
| Pky | 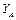
| – | – 
| – 
| – | |||
MA (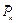 ) )
| 
| 
| 
| 
| 
| - 
|
Суммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:



5) Решим полученную систему уравнений и найдем:
из 1-го
 кН;
кН;
из 2-го
 кН;
кН;
из 3-го

 кН·м.
кН·м.
Знак «минус» у реакции XA указывает на то, что эта реакция в действительности направлена в сторону, противоположную ранее принятой (см. рис. 3.6.).
По составляющим реакции в шарнире А можно определить ее модуль и направление
 кН,
кН,

где β – угол, между вектором реакции  и положительным направлением оси x.
и положительным направлением оси x.
Для проверки полученного решения составим выражение суммы моментов всех сил, например, относительно точки В:


В данном примере относительная погрешность оказалась равной нулю.
Пример 3. Определить реакцию шарнира A и усилие в идеальном стержне BC балки (рис. 3.7.), нагруженной равномерной распределенной нагрузкой интенсивностью q = 4 кН/м и удерживающей груз весом P = 6 кН с помощью троса. Он переброшен через неподвижный блок В. Трение в блоке отсутствует. Размеры на рисунке даны в метрах. Точки A, B и D считать расположенными на одной прямой.

Решение
1) В качестве объекта равновесия примем балку AD.
2) Активными силами, действующими на объект равновесия, будут сила  , направленная вдоль нити в месте крепления, и сила
, направленная вдоль нити в месте крепления, и сила 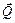 , которая является равнодействующей распределенной нагрузки q и модуль которой
, которая является равнодействующей распределенной нагрузки q и модуль которой  кН.
кН.
3) Отбрасывая связи (неподвижный цилиндрический шарнир A и идеальный стержень BC), заменим их действие на объект равновесия реакцией  . Она представлена составляющими
. Она представлена составляющими 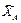 и
и 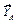 , параллельными координатным осям, и усилием в стержне
, параллельными координатным осям, и усилием в стержне  , которое направлено по прямой, соединяющей шарниры B и C.
, которое направлено по прямой, соединяющей шарниры B и C.
4) Запишем уравнения равновесия (3.2) полученной плоской системы сил в принятой системе координат (см. рис. 3.7), составив предварительно табл. 3.3.
Таблица 3.3
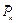
| 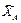
| 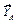
| 
| 
| 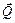
|
| Pkx | 
| 
| 
| ||
MA (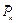 ) )
| 
| 
| 
| ||
MB (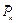 ) )
| 
| 
| 
|
Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:



5) Решим полученную систему уравнений и найдем:
из 2-го
 кН;
кН;
из 1-го

 кН;
кН;
из 3-го
 кН.
кН.
Знак «минус» у реакции XA указывает на то, что эта реакция в действительности направлена в сторону, противоположную ранее принятой (см. рис. 3.7).
Для проверки полученного решения составим выражение суммы проекций всех сил на ось y:


В данном примере относительная погрешность также оказалась равной нулю.
Вопросы для самоконтроля
1. Какую совокупность сил называют произвольной плоской системой сил?
2. Как определяют алгебраический момент силы относительно точки?
3. Что называют плечом силы относительно точки?
4. Как принято устанавливать знак алгебраического момента силы относительно точки?
5. Когда удобно использовать теорему Вариньона для нахождения момента силы относительно точки?
6. Какую систему сил называют парой сил и как определяют алгебраический момент пары сил?
7. Какими основными свойствами обладает пара сил?
8. Какую эквивалентную замену применяют для равномерно распределенной нагрузки?
9. Как записывают условия равновесия произвольной плоской системы сил в основной и в дополнительных формах?
10. Выполнение каких условий необходимо для разрешимости уравнений равновесия?
11. Каким образом можно проверить правильность решения задачи и оценить его точность?
Не нашли, что искали? Воспользуйтесь поиском: