Примеры решения типовых задач. Пример 1. Определить из условий равновесия реакции подпятника A, неподвижного цилиндрического шарнира B и величину силы для невесомого вертикального вала AB

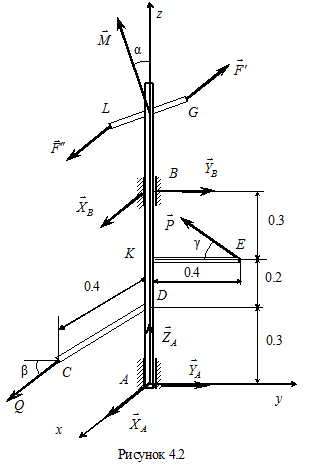
Пример 1. Определить из условий равновесия реакции подпятника A, неподвижного цилиндрического шарнира B и величину силы 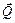для невесомого вертикального вала AB (рис. 3.2), к которому жестко прикреплены стержни CD и KE, расположенные в плоскостях, перпендикулярных оси z, причем стержень CD параллелен оси x, а стержень KE – оси y. Конструкция нагружена силами и 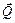, причем сила , кН расположена в плоскости, перпендикулярной оси z, и составляет с осью стержня KE угол γ = 30⁰, а сила 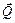– в плоскости, перпендикулярной оси x, и составляет с горизонталью угол β = 60⁰. Кроме того, к концам стержня LG, жестко прикрепленного к валу и расположенного в плоскости yOz, приложены две равные, противоположно направленные силы и , параллельные оси x и образующие пару сил. Вектор-момент этой пары 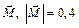кН·м расположен в плоскости yOz и составляет с осью z угол α = 30⁰. Размеры на схеме даны в метрах.

Решение

1) Объектом равновесия является вся конструкция (вал с прикрепленными к нему стержнями).

2) Активными силами, действующими на объект равновесия, будут силы , 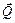и пара сил, вектор-момент которой .

3) Отбрасывая связи (подпятник A и неподвижный цилиндрический шарнир B), заменим их действие на объект равновесия реакциями и 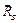. Реакция подпятника представлена составляющим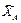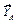и , и 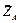, а неподвижного цилиндрического шарнира – составляющим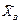и и 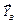, параллельными соответствующим координатным осям.

4) Запишем уравнения равновесия (4.4) полученной пространственной системы сил в принятой системе координат (см. рис. 4.2) с помощью табл. 4.1.

Таблица 4.1

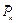
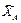
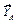
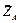
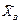
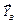
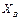
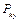
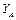
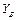
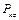
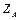
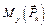
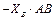
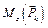
Продолжение табл. 4.1

			–
			–
			–

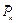
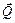
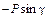
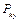
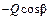
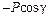
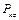
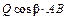
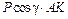
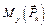
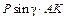
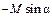
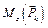
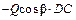
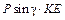
Рассмотрим более подробно определение момента силы относительно оси на примере силы (см. рис. 4.2).

Способ 1. Определим проекции силы :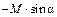

– на плоскость, перпендикулярную оси x,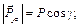

– на плоскость, перпендикулярную оси y,

– на плоскость, перпендикулярную оси z,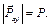

При определении моментов силы относительно осей x и y плечом будет одно и то же расстояние AK. Поэтому с учетом знаков получим

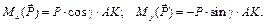
При определении моментов силы относительно оси z учтем, что сила уже расположена в плоскости, перпендикулярной этой оси. Точка пересечения этой плоскости с осью – это точка К. Для нахождения алгебраического момента силы относительно этой точки воспользуемся теоремой Вариньона

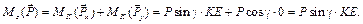
Способ 2. Запишем проекции силы на оси координат:

и координаты точки приложения силы – точки E:

Используя аналитические выражения (4.2), получим

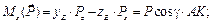
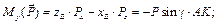
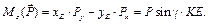
Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:

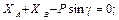
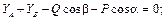
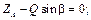
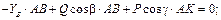
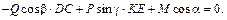
5) Решим полученную систему, начиная с уравнений, содержащих не более одной неизвестной силы. Так, из последнего уравнения определим

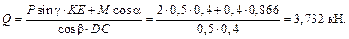
Затем с учетом найденного значения Q решим 5-е уравнение и определим

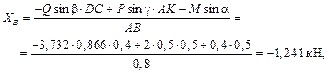
Далее из уравнений находим:

из 1-го

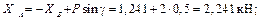
из 3-го

из 4-го

и, наконец, из 2-го

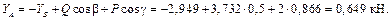
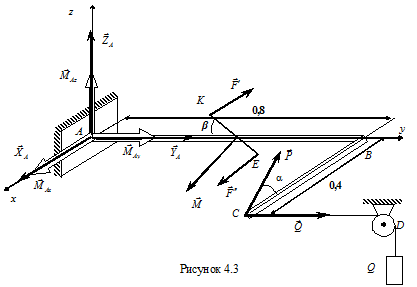
Пример 2. Определить реакции жесткой пространственной заделки А для невесомой рамы ABC (рис. 4.3.), расположенной в горизонтальной плоскости xOy и нагруженной силой , силами и , образующими пару сил, вектор-момент которой , 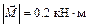. Кроме того, с помощью троса, переброшенного через неподвижный блок D и прикрепленного к концу С рамы, удерживается в равновесии груз весом 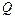= 2 кН. Сила расположена в плоскости, перпендикулярной оси y, и составляет с прямой BC угол α = 30⁰ . Стержень KE, к концам которого приложены силы пары, параллельные оси x, жестко прикреплен к раме и расположен в плоскости yOz под углом β = 60⁰ к оси y. Прямая CD параллельна оси y. Размеры на схеме даны в метрах.

Решение

1) Объектом равновесия является рама ABC.

2) Активными силами, действующими на объект равновесия, будут силы , 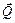(сила натяжения троса, удерживающая груз Q) и пара сил, вектор-момент которой .

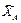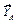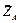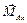3) Отбрасывая связь – жесткую пространственную заделку А, заменим ее действие на объект равновесия реакцией , представленной составляющими , и , и вектором-моментом , представленным составляющими , и .

4) Запишем уравнения равновесия (4.4) полученной пространственной системы сил в принятой системе координат (см. рис. 4.3), составив табл. 4.2.

Таблица 4.2

				–
				–
				–

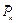
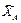
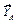
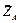
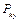
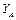
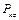
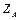
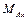
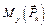
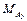
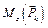
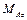
Продолжение табл. 4.2

			–
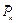
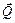
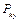
	Q		–
			–

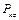
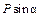
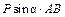
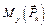
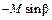
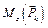
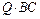
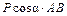
Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:

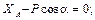
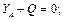
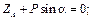
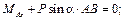
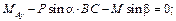
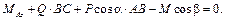
5) Решим полученную систему:

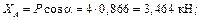
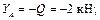
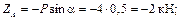
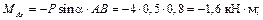
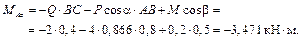
Пример 3. Определить силы натяжения тросов, удерживающих в горизонтальном положении однородную пластину ABC, имеющую форму равностороннего треугольника, на которой находится точечный груз (рис. 4.4.). Длина стороны пластины a = 100 см, ее вес G = 0,2 кН. Вес точечного груза P = 5 кН. Координаты точки 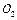, в которой расположен груз: 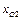= 15 см, 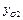= 25 см.

Решение

1) Объектом равновесия является пластина ABC.

2) Активными силами, действующими на объект равновесия, будут и .

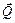3) Отбрасывая связи, т.е. рассекая тросы, на которых подвешена

пластина, заменим их действие на объект равновесия силами натяжения 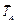, 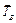и .

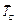4) Запишем уравнения равновесия (4.4) полученной пространственной системы сил в принятой системе координат (см. рис. 4.4). Предварительно определим координаты точки О ₁ – точки приложения равнодействующей силы тяжести пластинки . Центр тяжести однородной треугольной пластины расположен в точке пересечения медиан треугольника. Поэтому для выбранной системы координат запишем координаты точки О ₁:

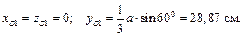
Следует учесть, что силы, действующие на объект равновесия, представляют собой систему параллельных сил в пространстве. Поэтому два первых и последнее уравнения удовлетворяются тождественно: проекции сил на оси x и y равны нулю, так как каждая из сил перпендикулярна этим осям и момент их относительно оси z равен нулю, поскольку линии действия сил параллельны оси z. Таким образом, для определения трех неизвестных реакций можно записать следующие уравнения равновесия:

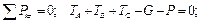
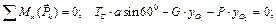
5) Решим полученную систему. Вначале из 2-го уравнения определим

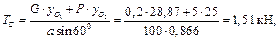
а затем, используя 3-е уравнение, выразим 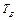через :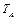

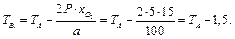
Подставляя полученные результаты в 1-е уравнение, получим

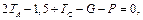
откуда

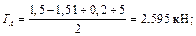
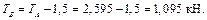
Вопросы для самоконтроля

1. Какую совокупность сил называют произвольной пространственной системой сил?

2. Чем характеризуется вращательное действие силы на тело, имеющее неподвижную ось?

3. Что называют моментом силы относительно оси?

4. Как определяют величину момента силы относительно оси?

5. Как определяют знак момента силы относительно оси?

6. В каких случаях момент силы относительно оси равен нулю?

7. Какие способы используют для определения момента силы относительно оси?

8. Чем в общем случае полностью определяется действие пары сил на твердое тело?

9. Чему равен модуль вектора-момента пары сил и как он направлен?

10. Какими свойствами обладает вектор-момент пары сил?

11. Как определить момент пары сил относительно оси?

12. Как записывают условия равновесия произвольной пространственной системы сил в векторной форме?

13. Как записывают условия равновесия произвольной пространственной системы сил в аналитической форме?

14. Каким условиям должна удовлетворять система уравнений равновесия для получения единственного решения?

Не нашли, что искали? Воспользуйтесь поиском: