ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ

Полярная система координат является примером наиболее употребительной криволинейной системы координат. Если совместить начала декартовой и полярной систем координат и направить полярную ось по положительному направлению оси абсцисс, то уравнения связи между системами координат имеют вид: или (в обратную сторону) . Полярный угол по положению точки на плоскости определяется неоднозначно с точностью до . По аналогии с соглашением, принятым при отыскании модуля и аргумента комплексного числа, примем: . Координатная сетка полярной системы координат похожа на мишень для дротиков (см. рис. 5). Лучи, исходящие из начала координат, это координатные линии, на которых постоянен полярный угол const, а концентрические окружности с центром в точке О − это координатные линии, на которых постоянен полярный радиус 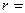const.

Формула замены переменных, связанная с переходом от декартовых координат к полярным, примет вид:

(8)

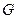где − образ области . Множитель 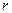равен якобиану преобразования:

Переход к полярной системе целесообразно выполнять, если:

1) границы области интегрирования описаны полярными уравнениями;

2) границы области D − дуги окружностей и отрезки прямых;

3) функция имеет вид: 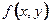= или =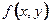

ИНТЕГРАЛ ПУАССОНА

Пример 3 (вывод значения интеграла Пуассона).В теории вероятностей широко используют несобственный интеграл 1-го рода , который называют интегралом Пуассона-Эйлера (кратко интегралом Пуассона). Он сходится к числу : = . Один из способов обоснования приведенной формулы интересен тем, что опирается на формулу замены переменных в двойном интеграле и описан ниже.

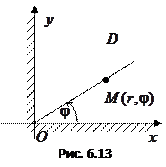Составим несобственный двойной интеграл 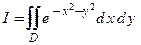, где − I-я четверть координатной плоскости (см. рис. 6), и исследуем его на сходимость. Напишем два представления этого интеграла.

Этот интеграл распространен на 1-ю четверть, где декартовы координаты изменяются в пределах: 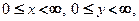а полярные координаты − в пределах: Двойной интеграл преобразуем в повторный:

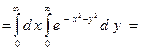
где 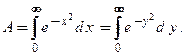Получен несобственный интеграл 1-го рода. Обратим внимание на тот факт, что неопределенный интеграл относится к числу неберущихся, и по этой причине найти его значение по обобщенной формуле Ньютона-Лейбница нельзя.

Итак, искомая величина Это первое представление

Затем вычислим несобственный двойной интеграл при помощи перехода к полярным координатам по формуле (8):

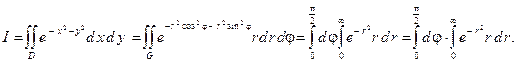
В данном случае повторный интеграл равен произведению определенного интеграла и несобственного интеграла 1-го рода. Определенный интеграл . Несобственный интеграл 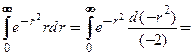Тогда 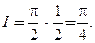Это второе представление

Приравняем первое и второе представления и получим уравнение: Таким образом, несобственный интеграл сходится и имеет значение: .

Подынтегральная функция − четная. Поэтому значения несобственных интегралов от этой функции по симметричным промежуткам 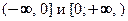равны. Отсюда следует, что интеграл Пуассона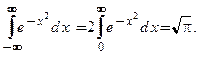

Не нашли, что искали? Воспользуйтесь поиском: