ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА

ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ

Площадь плоской измеримой фигуры вычисляется в декартовых и полярных координатах по формулам:

(9)

(10)

Объем цилиндроида, ограниченного сверху поверхностью снизу областью с боков − цилиндрической поверхностью, образующая которой параллельна оси , вычисляется по формуле:

. (11)

Площадь поверхности, заданной явно уравнением , где 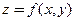− функция, дифференцируемая в измеримой области , вычисляется по формуле:

(12)

где [Кудрявцев].

Ранее были найдены площади плоских фигур по формулам (9) и (10), а затем значение двойного интеграла был найдено как объем цилиндроида по формуле (11), прочитанной справа налево.

Выведем формулу для площади круга при помощи двойного интеграла.

Пример 4. Найти площадь круга с радиусом .

□ Поместим центр круга в общее начало О декартовой и полярной систем координат (см. рис. 7). Уравнение окружности, ограничивающей круг, в декартовых координатах имеет вид: . Полярное уравнение этой окружности: Тогда площадь круга вычисляется по формуле (10): . Перейдем от двойного интеграла в полярных координатах к повторному. Чтобы расставить пределы интегрирования в повторном интеграле, заметим, что каждый луч, исходящий из полюса О имеет с кругом общий отрезок − радиус окружности. Отсюда делаем вывод, что на каждом луче значения При изменении угла в пределах от 0 до этот луч ометает всю область интегрирования − весь круг. Расставляем пределы интегрирования и получаем:

■

ЭКОНОМИЧЕСКИЕ ПРИЛОЖЕНИЯ

Двойной интеграл, как и определенный, можно использовать для описания и анализа характеристик производства промышленной и сельскохозяйственной продукции, для определения ресурсов территорий (природных, трудовых и других), для расчета энергии, потребляемой неким регионом и в других случаях.

Ресурсы территории по известной плотности их распределения могут быть вычислены по формуле:

(13)

где − декартовы координаты точки территории .

Средняя плотность распределения ресурсов по территории равна

(14)

Не нашли, что искали? Воспользуйтесь поиском: