Периодические десятичные дроби

Периодическая десятичная дробь — это любая десятичная дробь, у которой:

1. Значащая часть состоит из бесконечного количества цифр;

2. Через определенные интервалы цифры в значащей части повторяются.

Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа.».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a / b. Разложим ее знаменатель на простые множители. Возможны два варианта:

1. В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным. Такие нас не интересуют;

2. В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

1. Сначала разделится целая часть, если она есть;

2. Возможно, будет несколько чисел после десятичной точки;

3. Через некоторое время цифры начнут повторяться.

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

Как видим, остатки повторяются. Запишем дробь в «правильном» виде:1,733... = 1,7(3).

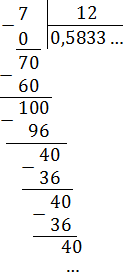
В итоге получается дробь: 0,5833... = 0,58(3).

Записываем в нормальном виде: 4,0909... = 4,(09).

Получаем дробь: 0,4141... = 0,(41).

Не нашли, что искали? Воспользуйтесь поиском: