Вычисление предела при .

Теоретическая часть:

1. Предел бесконечно малой равен нулю.
2. Если предел величины равен нулю, то эта величина есть бесконечно малая.
3. Предел бесконечно большой величины равен бесконечности.
4. Если 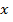- величина бесконечно малая, то обратная ей величина является бесконечно большой.
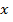5. Если - величина бесконечно большая, то обратная ей величина является бесконечно малой.
6. Предел числа есть само число.
7. Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.

Разбор решения одного варианта:

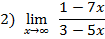
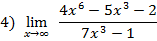
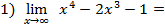первые два слагаемых пределов не имеют, поэтому имеет место неопределенность , чтобы её раскрыть, надо

вынести за скобку большую степень переменной, входящей в пример:

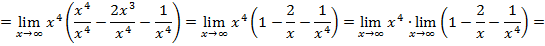
величины

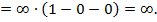
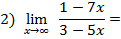
предел числителя и предел знаменателя есть величины бесконечно большие 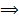имеет место неопределенность вида 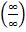, раскроем её делением числителя и знаменателя на наибольшую степень переменной т.е. на 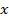и сократим, тогда

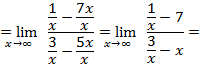
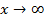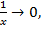
помня, что при , , 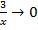имеем

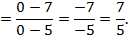
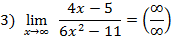
делим каждое слагаемое на сократим

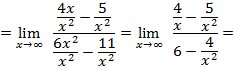
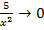, , , имеем:

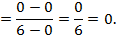
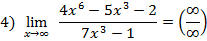
делим числитель и знаменатель на старшую степень переменной, это :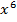

, , , ,

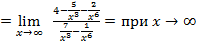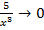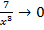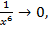
тогда предел числителя равен 4, 0, т.е. в знаменателе бесконечно малая величина 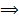вся дробь есть величина бесконечно большая, т.е. = .

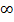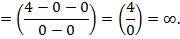
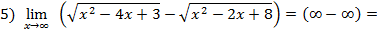
умножим на сопряженный

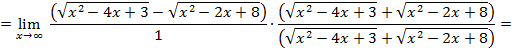
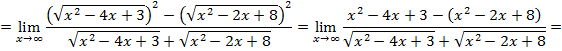
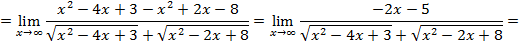
при 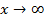, имеем 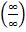, раскроем путем деления на 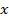, т.к. :

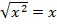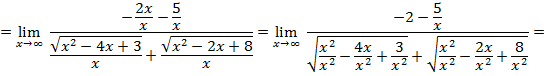
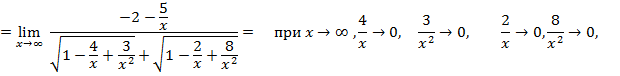
тогда: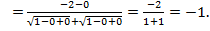

Не нашли, что искали? Воспользуйтесь поиском: