Примеры исследования функций и построения графиков.

Пример 1. Построим график функции .

1) Функция -- многочлен, а у всех многочленов область определения -- вся вещественная ось. .

2) Многочлены бывают чётными функциями, если содержат только чётные степени переменного , и нечётными функциями, если содержат только нечётные степени . Для функции это не так, значит, не является ни чётной, ни нечётной функцией.

Периодическими из всех многочленов бывают только постоянные, то есть не зависящие от ; в нашем случае это не так, поэтому -- не периодическая функция.

3) Вертикальных асимптот график не имеет, поскольку область определения не имеет граничных точек. (У графиков многочленов вообще не бывает вертикальных асимптот.)

4) Поскольку многочлен имеет степень 3 (а не 1 или 0), то его график не имеет наклонных или горизонтальных асимптот.

5) Пересечение с осью найдём, вычислив значение при : имеем . Для нахождения пересечений графика с осью следует решить уравнение . Целых корней это уравнение не имеет. Вычисляя значения в некоторых целых точках, например,

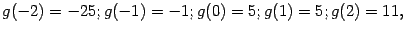
мы начинаем подозревать, что уравнение имеет только один корень , лежащий на интервале , причём ближе к точке , чем к 0. (Действительно, если применить какой-либо из методов приближённого нахождения корней алгебраического уравнения, мы получим, что ). Заметим, что меняет знак с на 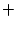при переходе через точку .

6) Производная данной функции равна 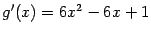. Найдём интервалы возрастания функции, решая неравенство . Корни квадратного трёхчлена - это , значит, решением неравенства служит объединение интервалов и . На каждом из этих интервалов функция возрастает. Интервалы убывания задаются обратным неравенством , то есть . Его решением служит интервал . На этом интервале функция убывает.

В точке возрастание функции сменяется убыванием, значит, -- точка локального максимума. Значение функции в этой точке равно

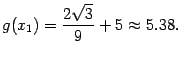
В точке убывание функции сменяется возрастанием, значит, -- точка локального минимума. Значение функции в этой точке равно

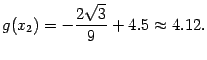
Как мы видим, на участке убывания значения функции изменяются от до и остаются положительными. Это доказывает, что сама функция действительно имеет только один корень.

7) Вторая производная функции равна . Для отыскания интервала выпуклости решим неравенство 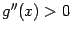, то есть , откуда . Значит, функция выпукла на интервале . Обратное неравенство даёт нам интервал вогнутости; очевидно, это . В точке направление выпуклости меняется, следовательно, -- это точка перегиба. Значение функции в этой точке равно .

8) С учётом предыдущих семи пунктов строим график функции .

График функции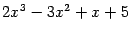

Пример 2. Исследуем функцию 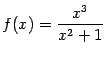и построим её график.

1). Поскольку знаменатель положителен при всех , область определения функции -- вся ось .

2). Функция -- нечётная, поскольку при смене знака числитель меняет знак, а знаменатель остаётся без изменения, откуда . Следовательно, график функции симметричен относительно начала координат.

Периодической функция не является.

3) Поскольку область определения этой элементарной функции -- вся вещественная ось, вертикальных асимптот график не имеет.

4) Найдём наклонные асимптоты при в виде . Имеем:

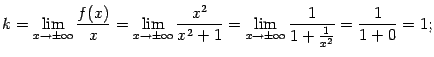
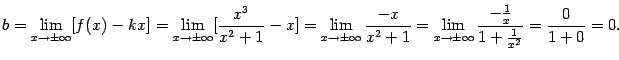
Таким образом, асимптотой как при , так и при служит прямая .

5) Найдём точки пересечения с осями координат. Имеем: , причём -- единственное решение уравнения . Значит, график пересекает сразу и ось , и ось в начале координат.

Очевидно, что при и при .

6) Найдём производную:

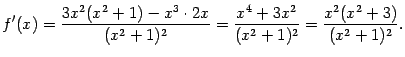
Очевидно, что при всех ; единственная точка, в которой -- это . Значит, функция возрастает на всей оси , а в стационарной точке имеет горизонтальную касательную.

7) Найдём вторую производную:

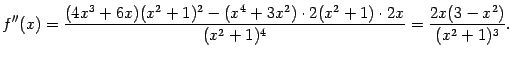
Знаменатель этой дроби положителен при всех . Числитель имеет корни и , при этом 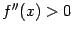на интервалах и -- на этих интервалах функция выпукла. На интервалах и 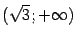выполняется обратное неравенство , здесь функция вогнута. Все три точки, в которых , то есть точки , являются точками перегиба.

8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции.

График имеет такой вид:

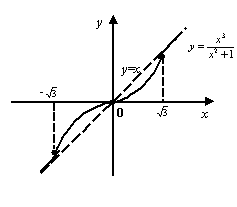
График функции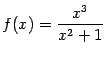

ПРАКТИЧЕСКАЯ РАБОТА.

Не нашли, что искали? Воспользуйтесь поиском: