Наименьших квадратов

Метод наименьших квадратов позволяет «подогнать» функцию под некоторый набор численных данных или, другими словами, построить график функций по некоторой ограниченной совокупности точек. Пусть требуется определить функцию 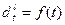, где - прогнозируемое значение рыночного спроса как некоторой зависимой переменной, а t- время как независимая переменная. Аппроксимирующая кривая, построенная методом наименьших квадратов, может иметь вид:

t₁ t₂ t₃ t₄ t₅ t₆ t₇

Выбор этой функции то считается наилучшим в том случае, когда оказывается сведенным к минимуму так называемое стандартное отклонение (т.е. квадратный корень из дисперсии, взятой с положительным знаком), определяемое формулой.

,

где

d_t – фактический спрос, наблюдаемый в t- й период (отрезок времени);

n – число периодов (или наблюдений),

f – число степеней свободы.

Минимизация S_dt эквивалента минимизации суммы квадратов разностей (Е)

® min

Задача прогнозирования рыночного спроса сводится к минимизации суммы квадратов разности между фактическим значением спроса в момент t и тем значением, которое принимает в данный момент прогнозирующая функция 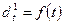. Это утверждение иллюстрируется графически представленное рисунком.

Чтобы определить вид прогнозирующей функции спроса необходимо нанести на плоскость системы координат t, значения фактического спроса d_t за 12 месяцев. Следует провести между смежными точками сглаживающую линию. Если получится, что наиболее близкая линия проведенная между этими точками, есть прямая, то будем искать аналитическое выражение нашей функции 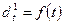в виде линейной функции (1). Неизвестными значениями являются коэффициенты a и b, их следует вычислить и подставить в уравнение (1) получив при этом функциональную зависимость, которая мало отличается от заданной .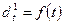

Запишем сумму квадратов разностей значений функций и

Исследуем эту функцию на наименьшее значение, произведя замену на уравнение (1)

Функция Е будет иметь наименьшее значение при тех ( при которых ее частные производные будут одновременно равны нулю. Подробные расчеты показаны на примере.

Не нашли, что искали? Воспользуйтесь поиском: