
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вопрос 10. Динамика автомобильного колеса.
При качении колеса по недеформируемой дороге на него действуют следующие силы: Р  - нормальная сила; Р
- нормальная сила; Р  - продольная сила колеса; М - крутящий момент. Сила Р
- продольная сила колеса; М - крутящий момент. Сила Р  называется силой тяги, если она направлена против движения и толкающей силой, если она направлена по движению. М подводится к колесу либо полуосью, либо от тормозного барабана. Со стороны опорной поверхности на колесо действуют : R
называется силой тяги, если она направлена против движения и толкающей силой, если она направлена по движению. М подводится к колесу либо полуосью, либо от тормозного барабана. Со стороны опорной поверхности на колесо действуют : R  - нормальная реакция, перпендикулярная опорной поверхности и направленная вверх, точка её приложения смещена вперед на величину а
- нормальная реакция, перпендикулярная опорной поверхности и направленная вверх, точка её приложения смещена вперед на величину а  ; R
; R  - продольная реакция, считается положительной, если направлена по движению, отрицательной, если направлена против движения. Рассмотрим условия равновесия: Т.к. j
- продольная реакция, считается положительной, если направлена по движению, отрицательной, если направлена против движения. Рассмотрим условия равновесия: Т.к. j 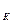 =j
=j  , то:
, то:
mj 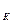 = R
= R  - P
- P 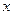 , откуда: Р
, откуда: Р  = R
= R  - mj
- mj 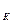 , (1.10)
, (1.10)
Пренебрегая неровностями дороги, считая её абсолютно гладкой: Р  =R
=R  . Если I
. Если I 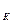 - момент инерции колеса относительно т. О:
- момент инерции колеса относительно т. О:
I 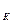 d
d 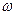 /dt=M - R
/dt=M - R  r
r  - R
- R  a
a  , откуда:
, откуда:
R  = M/r
= M/r  - R
- R 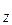 a
a  /r
/r  - I
- I 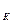 /r
/r  d
d  d t, (1.11)
d t, (1.11)
Колесо, механизм, преобразующий вращательное движение в поступательное. Как в любом механизме здесь есть потери. Их можно найти по разности мощностей (N  - N
- N  ), где: N
), где: N  - мощность, подводимая к колесу; а N
- мощность, подводимая к колесу; а N  - мощность, передаваемая от колеса к автомобилю.
- мощность, передаваемая от колеса к автомобилю.
N  = M
= M  , а N
, а N  = P
= P 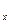 V
V  , подставляя в выражение разности уравнения (1.10) и (1.11), группируя члены получим:
, подставляя в выражение разности уравнения (1.10) и (1.11), группируя члены получим:
N  - N
- N  = M (r
= M (r 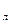 -r
-r  )/r
)/r 
 + a
+ a  R
R 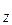 r
r 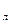 /r
/r 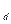
 + (I
+ (I 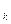 /r
/r 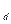 +m
+m  r
r 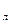 )j
)j 
 , (1.12)
, (1.12)
Первая часть выражения (1.12) отражает собой потери на качение:
N  = (M*(r
= (M*(r 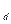 - r
- r 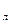 )/r
)/r 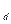 + a
+ a  R
R 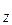 r
r 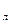 /r
/r 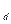 )
)  , (1.13)
, (1.13)
А вторая потери, связанные с изменением кинетической энергии колеса:
N  = (I
= (I 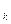 /r
/r 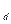 + m
+ m 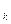 r
r 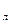 )j
)j 
 , (1.14)
, (1.14)
Потери, связанные с изменением кинетической энергии колеса, существуют только при наличии j  .
.
N 
 - это безвозвратные потери мощности, возникающие при качении, эту мощность принято называть мощностью сопротивления качению.
- это безвозвратные потери мощности, возникающие при качении, эту мощность принято называть мощностью сопротивления качению.
Поделив выражение (3) на  , получим выражение для момента сопротивления качению:
, получим выражение для момента сопротивления качению:
М  = М(r
= М(r 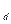 - r
- r 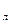 )/r
)/r 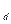 + а
+ а  R
R 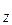 r
r 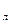 /r
/r 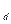 , (1.15)
, (1.15)
Поделив выражение (5) на r 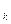 получим выражение для силы сопротивления качению:
получим выражение для силы сопротивления качению:
Р  = М/r
= М/r 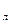 (r
(r 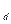 -r
-r 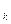 )/r
)/r 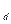 + a
+ a  R
R 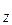 /r
/r 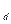 , (1.16)
, (1.16)
Если теперь выражение (6) поделить на R  , то получиться некоторое
, то получиться некоторое  выражение, определяющее условную количественную величину называемую коэффициентом сопротивления качению f:
выражение, определяющее условную количественную величину называемую коэффициентом сопротивления качению f:
f = а  /r
/r 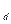 + M/ R
+ M/ R 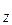 (r
(r 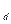 - r
- r 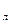 )/r
)/r 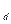 r
r 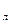 , (1.17)
, (1.17)
f выражает собой энергетические потери колеса. Причем первая часть выражения (7) отражает собой силовые потери, связанные с наличием смещения нормальной реакции, которое вызывает появление момента направленного против движения: f  = а
= а  /r
/r 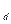 , а вторая часть выражения (6) отражает собой кинематические потери, связанные с уменьшением радиуса качения при передаче тягового момента, что приводит к уменьшению линейной скорости колеса V
, а вторая часть выражения (6) отражает собой кинематические потери, связанные с уменьшением радиуса качения при передаче тягового момента, что приводит к уменьшению линейной скорости колеса V  при неизменной угловой скорости
при неизменной угловой скорости  .
.
Анализируя выражения (1.12), (1.13) и (1.14) получим:
N  - N
- N  = N
= N  +N
+N  или N
или N  = N
= N  + N
+ N  +N
+N  , (1.18)
, (1.18)
Выражение (1.18) отражает собой энергетический баланс колеса. Поделив обе части выражения на скорость V  , получим силовой баланс колеса:
, получим силовой баланс колеса:
Р  = Р
= Р  + Р
+ Р  + Р
+ Р  , (1.19)
, (1.19)
Полезную силу иначе называют силой тяги. Сравнивая выражения (1.11) и (1.19) получаем, что Р  = М/r
= М/r 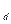 , подставляя сюда значение М при V
, подставляя сюда значение М при V  = 0 имеем:
= 0 имеем:
Р  = Р
= Р  = М
= М 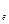 u
u 
 /r
/r 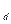 , (1.20)
, (1.20)
При расчетах вместо r 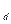 используют r
используют r 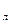 .
.
Не нашли, что искали? Воспользуйтесь поиском: