
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Критерии качества измерений
Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также размером допустимых погрешностей.
Точность — это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Высокая точность измерений соответствует малым погрешностям как систематическим, так и случайным.
Точность количественно оценивают обратной величиной модуля относительной погрешности. Например, если погрешность измерений равна iO~G, то точность равна 106.
Достоверность измерений характеризует степень доверия к результатам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики. Это дает возможность для каждого конкретного случая выбирать средства и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ с необходимой достоверностью.
Под правильностью измерений понимают качество измерений, отражающее близость к нулю систематических погрешностей в результатах измерений.
Сходимость — это качество измерений, отражающее близость друг к другу результатов измерений одного и того же параметра, выполненных повторно одни-
ми и теми же средствами одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость — это такое качество измерений, которое отражает близость друг к другу результатов измерений, выполняемых в различных условиях (в различное время, в различных местах, различными методами и средствами).
3.5 Классом точности называется обобщенная характеристика средств измерений, определяемая пределами допускаемой основной (а иногда и дополнительной)погрешности. Правила установления классов точности содержатся в ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования».
Классы точности указываются в частных стандартах (технических условиях), содержащих конкретные технические требования к тем или иным типам средств измерений. Если средство измерений предназначено для измерений нескольких величин (например, для измерения электрических напряжения и сопротивления), то класс точности определяется для каждой из величин. Так же определяется класс точности для средств измерений, имеющих несколько диапазонов измерений: каждый диапазон имеет свой класс точности.
Присваиваются классы точности средствам измерений при их разработке (по результатам приемочных испытаний). В связи с тем, что в процессе эксплуатации средств измерений их метрологические характеристики обычно ухудшаются, допускается понижать класс точности по результатам поверки (калибровки) средства измерений.
Основой для определения класса точности прибора является характер изменения основной абсолютной погрешности средства измерений.
1. Если основная абсолютная погрешность имеет аддитивный характер, т. е. границы погрешностей измерительного прибора не изменяются в пределах диапазона измерений (рис. 6.18, а), то класс точности представляется пределами допускаемой приведенной погрешности.
γ = ± ∆ \ XN *100 = ± Р, %
где ∆ = ± а — пределы допускаемой основной абсолютной погрешности прибора; р — отвлеченное положительное число, выбираемое из ряда предпочтительных чисел:1*10; 1,5*10n; 1,6*10n; 2*10n; 2,5*10n; 3; 4; 5; 6; (n=1; 0; -1; -2; -3; и т.д.) XN — нормирующее значение, выраженное в единицах абсолютной погрешности. Под нормированием понимается установление границ на допустимые отклонения реальных метрологических характеристик средств измерения от их номинальных значений
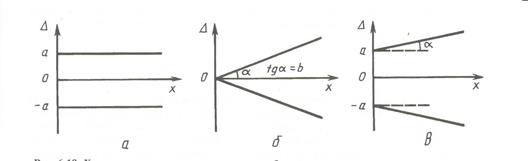
Рис. 6.18. Характерные случаи изменения границ абсолютных погрешностей средств измерений
2. Если основная абсолютная погрешность имеет мультипликативный характер, т. е. границы погрешностей измерительного прибора линейно изменяются в пределах диапазона измерений (рис. 6.18, б), то класс точности представляется пределами допускаемой относительной погрешности γγ δ в виде.
δ = ± (∆ \ х) * 100 = ±q, %
(где ∆ = ± Ьх — пределы допускаемой основной абсолютной погрешности прибора (b = tg а); х — показания прибора (без учета знака измеренной величины); q — отвлеченное положительное число.
СТР136-137
Кузнецов
3. Если основная абсолютная погрешность имеет аддитивный и мультипликативный характер, т. е. границы погрешностей измерительного прибора линейно изменяются в пределах диапазона измерений (рис. 6.18, в), то класс точности представляется пределами допускаемой относительной погрешности δ в виде.
δ = ± (∆ \ х) * 100 = ±q, %
(где ∆ = ±(а+ b х) — пределы допускаемой основной абсолютной погрешности прибора (b = tg а); х — показания прибора (без учета знака измеренной величины); q — отвлеченное положительное число.
3.6 Обозначение классов точности. Если пределы допускаемой основной погрешности выражены в форме абсолютной погрешности средства измерений, то класс точности в документации и на средстве измерений обозначается прописными буквами римского алфавита (соответствие букв значению абсолютной погрешности раскрывается в технической документации на соответствующие средства измерений). Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, присваиваются буквы, находящиеся ближе к началу алфавита. Подобным же образом обозначаются классы точности средств измерений, для которых пределы допускаемой основной погрешности установлены в виде формулы, таблицы, графика, не соответствующих формулам (6.75)... (6.77).
Примеры обозначения классов точности в документации и на средстве измерений приведены в табл. 6.2.
| Таблица | 6.2 | ||||||
| Форма выражения погрешности | Номер формулы, по которой определяются пределы допускаемой основной погрешности | Пределы допускаемой основной погрешности, % | Обозначение класса точности | ||||
| в документации | на средстве измерений | ||||||
| Приведенная погрешность γ | По формуле (6.75): если нормирующее значение XN выражено в единицах измеряемой величины; если нормирующее значение принято равным длине шкалы (существенно нелинейная шкала) | γ =± 1,5 γ =±0,5 | 1,5 0,5 | 1,5 0,5 | |||
| Относительная погрешность б | По формуле (6.76) По формуле (6.77) | 6 = 5= + | ± 1,5 0,05 + 0,02 | X N | 1,0 0,005/ 0,002 | (1,0) 0,005/ 0,002 | |
| X | |||||||
| Абсолютная погрешность ∆ | По формуле ∆ = ± а или ∆ = ± (а+ b х) | м | М |
Вопросы для самопроверки.
1. Как звучит основной постулат метрологии?
2. Чем различаются ошибки систематические и случайные?
3. Какова сущность погрешностей абсолютных и относительных, статических и динамических? Как их следует учитывать в результатах измерений?
4. Какие факторы влияют на возникновение погрешностей?
Не нашли, что искали? Воспользуйтесь поиском: