
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ФУНКЦИЯ КОББА-ДУГЛАСА. ИЗОКВАНТЫ
Рассмотрим функцию 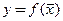 , определенную на множестве
, определенную на множестве  Поверхностью уровня функции
Поверхностью уровня функции 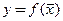 называют множество точек, в которых функция принимает одно и то же постоянное значение
называют множество точек, в которых функция принимает одно и то же постоянное значение  При заданном значении
При заданном значении  уравнение
уравнение  – это уравнение поверхности уровня. Число
– это уравнение поверхности уровня. Число  называют уровнем. В пространстве
называют уровнем. В пространстве 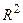 вместо поверхностей рассматривают линии уровня. Линии и поверхности уровня расположены в области определения функции.
вместо поверхностей рассматривают линии уровня. Линии и поверхности уровня расположены в области определения функции.
 Пример 1. Построить линии уровня функции
Пример 1. Построить линии уровня функции 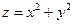 .
.
□ Линии уровня  представляют собой окружности
представляют собой окружности  , если
, если  , с радиусом
, с радиусом 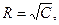 и точку
и точку  при
при  . Линий уровня, соответствующих отрицательным значениям С, нет, так как значения функции неотрицательны. На рис.1 приведены линии уровня для значений
. Линий уровня, соответствующих отрицательным значениям С, нет, так как значения функции неотрицательны. На рис.1 приведены линии уровня для значений  , равных
, равных  ■
■
Для функции  уравнением поверхности уровня, проходящей через точку
уравнением поверхности уровня, проходящей через точку  является уравнение
является уравнение  . После упрощения оно принимает вид
. После упрощения оно принимает вид 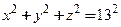 и описывает сферу с центром в начале координат и радиусом
и описывает сферу с центром в начале координат и радиусом  В каждой точке этой сферы значение функции
В каждой точке этой сферы значение функции  равна одному и тому же числу:
равна одному и тому же числу: 
Линии уровня функции Кобба-Дугласа  (
( ) называют изоквантами. Они расположены в плоскости
) называют изоквантами. Они расположены в плоскости 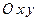 . Каждая точка изокванты соответствует комбинации ресурсов, при которой фирма выпускает заданный объем продукции. Набор изоквант, характеризующий данную производственную функцию, называют картой изоквант.
. Каждая точка изокванты соответствует комбинации ресурсов, при которой фирма выпускает заданный объем продукции. Набор изоквант, характеризующий данную производственную функцию, называют картой изоквант.
Пример 2. Построить изокванту производственной функции Кобба-Дугласа  проходящую через точку, где
проходящую через точку, где  .
.

|
 Изокванта описывается уравнением:
Изокванта описывается уравнением:  или
или 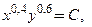 где
где  − объем выпуска продукции при заданных
− объем выпуска продукции при заданных
факторах:  . Найдем
. Найдем  :
: 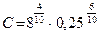 , или С
, или С  Подставим
Подставим 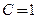 в уравнение изокванты, после чего получим прямую зависимость вложенного капитала от труда:
в уравнение изокванты, после чего получим прямую зависимость вложенного капитала от труда: 
|
 является кривая, похожая на гиперболу (см. рис. 2). Эта линия проходит через заданную точку (8; 0,25). В каждой точке построенной изокванты функция Кобба-Дугласа принимает одно и тоже значение, равное единице. С ростом
является кривая, похожая на гиперболу (см. рис. 2). Эта линия проходит через заданную точку (8; 0,25). В каждой точке построенной изокванты функция Кобба-Дугласа принимает одно и тоже значение, равное единице. С ростом 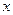 функция быстро убывает, а при
функция быстро убывает, а при 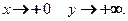
Как видно из графика изокванты, существует бесконечное множество комбинаций труда и капитала, обеспечивающих заданный объем выпуска  . ■
. ■
Не нашли, что искали? Воспользуйтесь поиском: