ПРОИЗВОДНАЯ СКАЛЯРНОГО ПОЛЯ ПО НАПРАВЛЕНИЮ

Рассмотрим функцию трех переменных 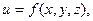определенную в некоторой окрестности точки и дифференцируемую в этой точке.

Функцию нескольких переменных можно дифференцировать не только по независимым переменным, но и по любому направлению, в частности, заданному вектором единичной длины (единичным вектором).

Проведем через точку полупрямую в направлении единичного вектора где − углы, которые вектор составляет с осями соответственно, Возьмем на полупрямой точку и подсчитаем приращение функции по направлению

Производной скалярного поля по направлению в точке называется предел отношения приращения функции по направлению к расстоянию при стремлении расстояния к нулю:

Параметрические уравнения прямой, проходящей через точку параллельно вектору , имеют вид [6]: При эти уравнения описывают изображенную на рисунке 3 полупрямую, исходящую из точки , причем точка с координатами находится от точки на расстоянии С учетом этих обстоятельств производная по направлению равна полной производной сложной функции 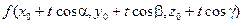в точке Применив правило дифференцирования к этой сложной функции и подставив получим формулу для производной по направлению:

(1)

В этой формуле множители 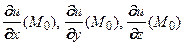являются координатами вектора , множители − координатами вектора . Тогда правая часть равна скалярному произведению векторов и [6]:

так как скалярное произведение векторов равно сумме произведений соответствующих координат векторов: . и Отсюда следует, что производная функции по направлению в точке равна величине проекции градиента на единичный вектор

или

, (2)

где − угол между градиентом и вектором .

Для функции двух переменных 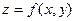производная в направлении единичного вектора вычисляется по формуле:

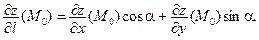
Понятие производной по направлению обобщается на функции произвольного числа переменных.

Пример 3. Вычислить производную функции в точке в направлении вектора где

□ Находим компоненты формулы (5.15): 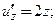в точке : Поэтому . Вектор

Единичный вектор заданного направления имеет координаты:

Вычисляем производную по направлению по формуле (1):

■

Производная по направлению в данной точке равна скорости изменения функции в заданном направлении. В этом состоит механический смысл производной по направлению.

Не нашли, что искали? Воспользуйтесь поиском: