ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ И ЕГО СВОЙСТВА

Если градиент функции отличен от нуля в заданной точке, то значение производной по направлению по формуле (5.13) напрямую зависит от косинуса угла .

Ясно, что наибольшее значение производной по направлению достигается при , когда направлением дифференцирования выбрано направление . Используя это соображение, можно сформулировать экстремальные свойства градиента.

1. В точке наибольшее значение производной по направлению равно модулю градиента:

где

2. В точке градиент определяет направление наибольшего роста функции:

.

Здесь для сокращения записи использовано второе обозначение градиента: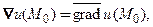

Заметим, что для функции двух переменных в приведенных формулах нужно исключить третьи компоненты; для функций четырех и большего числа переменных наоборот нужно добавить компоненты.

Пример 4. Найти направление наибольшего роста функции в точке 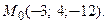Вычислить производную заданной функции в этом направлении в точке

□ Используем экстремальные свойства градиента. Направление наибольшего роста

(см. пример 1).

Производная по направлению равна 26:

■

Не нашли, что искали? Воспользуйтесь поиском: